ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Работа и мощность электрического тока. Закон Джоуля - Ленца
Общеизвестен факт, что ток при прохождении по проводникам нагревает их. Опыт 9.1.Закон Джоуля – Ленца[8,9] Оборудование: 1. Спираль нихромовая для электроплитки. 2. Штатив универсальный. 3. Стержень от изолирующего штатива. 4. 5. Шнур соединительный с вилкой. 6. Провод соединительный.
Рис. 9.1. Ход работы. 1.Соберем установку согласно рисунку 9.1. 2.Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд. Это равносильно тому, что заряд переносится за время t из одного конца проводника в другой. При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу 3.В случае, когда проводник неподвижен и химических превращений в нём не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Вывод: проводник под действием электрического тока нагревается. Количество теплоты, которое выделяется в проводнике, определяется по закону Джоуля - Ленца, математическая формулировка которого записывается так:
Различные формулы для записи закона Джоуля – Ленца получены путём подстановки вместо одной из переменных её выражение из закона Ома для участка цепи. Мощность тока измеряется количеством теплоты в единицу времени, т.е.:
Разветвление цепи Электрические цепи могут разветвляться. Участок цепи, в котором сходятся более двух проводников, называется узлом. Промежутки между узлами – суть ветви цепи. Возможны два вида соединения проводников. Последовательное соединение проводников.
Рис. 9.2.
Параллельное соединение проводников
Рис. 9.3.
По закону Ома для участка цепи:
В общем случае применение закона Ома для разветвленной цепи представляет собой известную трудность, поэтому на практике часто используют правила Кирхгофа. Правила Кирхгофа Существует два типа задач, встречающихся при расчёте разветвлённых электрических цепей постоянного тока. Первый тип задач: зная параметры электрической цепи (сопротивления и ЭДС), рассчитать токи и напряжение на её участках. Второй тип задач: зная токи и напряжения, рассчитать её параметры. В основе всех методов расчёта разветвлённых электрических цепей постоянного тока лежат правила Кирхгофа. 1. Алгебраическая сумма токов, сходящихся в узле, равна нулю, причем токи, входящие в узел, берутся со знаком "плюс", а выходящие – со знаком "минус". Это правило является прямым следствием закона сохранения электрического заряда:
Пример 1.(см. рис. 9.4)
Рис. .9.4. I1-I2+I3-I4=0. 2. Алгебраическая сумма падений напряжения на участках контура равна алгебраической сумме ЭДС, действующих в нем. Если ток или ЭДС совпадают с направлением обхода вдоль контура, то они берутся со знаком "+", в противном случае – со знаком "-" :
Пример 2.(см. рис. 9.5)
Рис. 9.5. I1r1+I1R1-I2R2+I3R3+I3r2-I4R4=E2-E1. Тесты к лекции №9. Тест 9.1.Отметьте уравнения, выражающие правила Кирхгофа: £
£
£
£
Тест 9.2.Для цепи какого тока действительны правила Кирхгофа в данной формулировке? £Постоянного тока. £ Переменного тока. £ Пульсирующего тока. £ Для цепей постоянного и переменного токов. Тест 9.3.Выделите формулы, характеризующие параллельное соединение проводников: £
£
£
£
£
Тест 9.4.К какому участку цепи можно применить первое правило Кирхгофа? £к узлам цепи. £ к любому выделенному в разветвленной цепи замкнутому контуру. £ ко всей цепи. £ к ветвям цепи. Тест 9.5.К какому из нижеприведенных элементов цепи можно применить второе правило Кирхгофа? £ к узлам цепи. £к любому выделенному в разветвленной цепи замкнутому контуру. £ ко всей цепи. £ к ветвям цепи. Понятие зоной теории проводимости. Контактная разность потенциалов. Термоэлектрические явления и их применение[11] 10.1. Понятие о зонной теории проводимости 10.2. Контактная разность потенциалов 10.3. Термоэлектрические явления и их применение |



 Реостат рычажный.
Реостат рычажный.


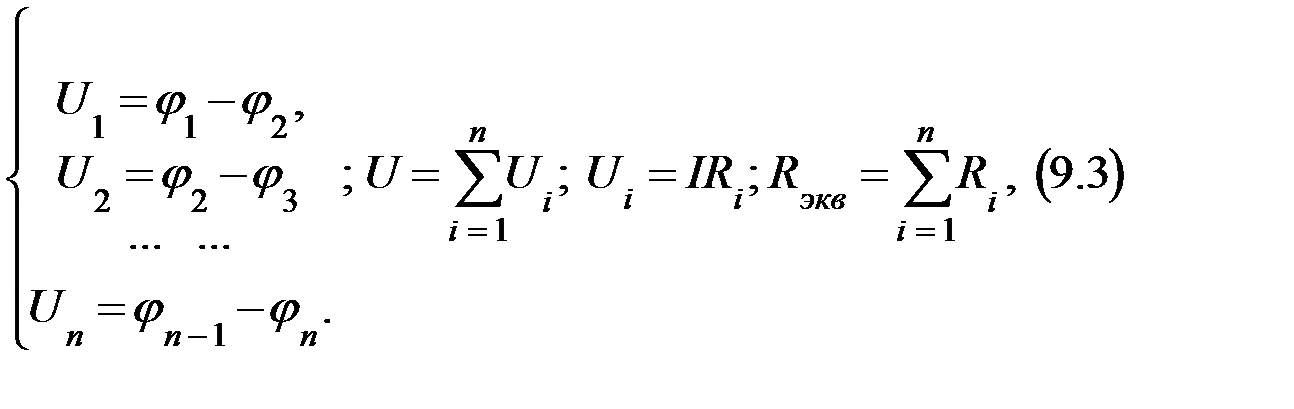


 ,
, .
.