 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| СВОЙСТВА (ПРИНЦИПЫ) ЛИНЕЙНЫХ ЦЕПЕЙ
ПОСТОЯННОГО ТОКА
Цель работы - освоение и экспериментальное подтверждение свойств линейных цепей, лежащих в основе методов их анализа.
Программа работы 1. Экспериментально убедиться в справедливости принципа наложения для токов в ветвях с источниками. 2. Экспериментально убедиться в справедливости принципа взаимности для какой-либо пары ветвей (рекомендуется взять те же ветви, что в п.1). Вычислить входную и взаимную проводимости по измерениям. 3. Используя ПК, рассчитать полную матрицу собственных и взаимных проводимостей исходной цепи. 4. Выделив какую-либо ветвь и представив оставшуюся часть цепи эквивалентным генератором, экспериментально найти его параметры: эквивалентную ЭДС ( 5. С помощью измерений токов в двух ветвях Пояснения к работе Данная лабораторная работа выполняется на стенде лабораторной работы N 2 для той же цепи. Пояснения приводятся также в виде примера расчета и «измерений» в прежней схеме (рис. 1) с параметрами:
Рис. 1. Графы цепей: а) исследуемой в лаборатории; б) рассматриваемой в примере.
П.1. При действии только источника
При действии только источника
При совместном действии
Рис. 2. Схемы к п.1 программы.
Так как направления стрелок токов
что с высокой точностью совпадает с результатами измерений (1.6=1.6; 2.2~2.19).
Примечание. При использовании принципа наложения для расчета токов можно поступать двояко: либо сохранить направление стрелок одинаковыми во всех схемах (исходной и при единственном источнике), либо при единственном источнике направлять стрелки так, чтобы токи получились положительными числами. В первом случае частные токи
П.2. Принцип взаимности. При действии единственной в цепи ЭДС
Примечание. 1. В цепи с единственным источником отношении
2. Если в п. 1 (принцип наложения) измерялись токи в ветвях с источниками, то проверка принципа взаимности не потребует других измерений, так как в линейной цепи с единственным источником тока и во всех ветвях прямо пропорциональны ЭДС: при увеличении (уменьшении) ЭДС в k раз все токи также увеличиваются (уменьшаются) в k раз. По измерениям в п. 1 имели
e3 = 20 В, Отсюда
что соответствует принципу взаимности.
П. 3. Расчет матрицы входных и взаимных проводимостей. Входной проводимостью называют Полная матрица проводимостей цепи (рис. 1), содержащей 5 ветвей («пустая» ветвь 6 исключена), имеет вид
Матрица с числовыми коэффициентами (для увеличения точности расчетов коэффициенты матрицы увеличены в 100 раз):
Зная матрицу
а в ветви 5
Эти результаты с высокой точностью совпадают с результатами расчетов (лаб.2, П.1). При компьютерном расчете матрицы а) указать для пассивной цепи стрелки токов во всех ветвях, затем включить в каждую ветвь б) составить расчетную систему уравнений Кирхгофа в общем виде; в) выполнить расчеты частных токораспределений по всем ветвям цепи от поочередного действия каждого (единственного) источника. При этом ток г) записать результаты расчета в виде таблицы (матрицы) проводимостей.
П. 4. Выделим ветвь 5, Определим параметры эквивалентного генератора методом ХХ и КЗ. Режим ХХ, Режим КЗ,
Рис. 3. Схемы к п. 4
Рассчитаем ток
что с высокой точностью совпадает со значением тока в п. 1 лаб. 2.
П. 5. Будем задаваться различными значениями сопротивления
Если
По этим экспериментальным данным можно найти зависимость тока
и убедиться в его справедливости при Из уравнений 1,5=a*1.5+в, 1,2=a*0.6+в. Находим Проверим справедливость этого равенства при Измерения в п. 1 лаб. раб. N 2 дали:
тогда выполняется приближенное равенство
Аналогично найдена зависимость На рис. 4 показаны зависимости
Рис. 4. Схемы к п. 5
Лабораторная работа N 3
|



 ) и эквивалентное внутреннее сопротивление (
) и эквивалентное внутреннее сопротивление (  ). Определение
). Определение  и
и 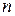 при изменении одного параметра цепи (
при изменении одного параметра цепи (  либо
либо  ), убедиться в справедливости свойства (принципа) линейности цепи. На основе измерений получить аналитическое выражение линейной зависимости
), убедиться в справедливости свойства (принципа) линейности цепи. На основе измерений получить аналитическое выражение линейной зависимости  . Построить график in=f(im).
. Построить график in=f(im). В,
В,  В,
В,  Ом,
Ом, 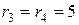 Ом,
Ом,  Ом
Ом
 , по месту включения эдс e3 поставлена закоротка), измерения дали (условно):
, по месту включения эдс e3 поставлена закоротка), измерения дали (условно):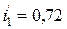 А,
А, 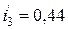 А.
А. , по месту действия эдс e1 поставлена закоротка) измеренные токи
, по месту действия эдс e1 поставлена закоротка) измеренные токи А,
А,  А.
А. и
и 
 А,
А,  А.
А.
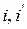 и
и  сохранялись неизменными для всех трех режимов, то истинные токи i1 и i3 равны
сохранялись неизменными для всех трех режимов, то истинные токи i1 и i3 равны ; i1=0,72+0,88=1.6 A
; i1=0,72+0,88=1.6 A ; i3=0,44+1,75=2.19 A
; i3=0,44+1,75=2.19 A и
и  суммируются со своими знаками; во втором - при несовпадении стрелки
суммируются со своими знаками; во втором - при несовпадении стрелки  А. При перемещении этой ЭДС в ветвь 3 (по стрелке i3), т.е.
А. При перемещении этой ЭДС в ветвь 3 (по стрелке i3), т.е.  В, ток в ветви 1 (по стрелке e3) при отсутствии других ЭДС получился равным
В, ток в ветви 1 (по стрелке e3) при отсутствии других ЭДС получился равным  А, т.е. при
А, т.е. при  имеет место равенство токов
имеет место равенство токов  , что и подтверждает принцип взаимности.
, что и подтверждает принцип взаимности. называют взаимной проводимостью между
называют взаимной проводимостью между  - взаимная проводимость между ветвями
- взаимная проводимость между ветвями  .
. См,
См, См,
См,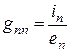 - коэффициент пропорциональности между током и ЭДС в ветви источника. Чтобы
- коэффициент пропорциональности между током и ЭДС в ветви источника. Чтобы  всегда получалось положительным числом, стрелки для
всегда получалось положительным числом, стрелки для 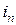 и
и 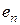 направляют одинаково (как это сделано для ветвей 1 и 3 на рис. 1). Взаимные проводимости могут быть и положительными и отрицательными.
направляют одинаково (как это сделано для ветвей 1 и 3 на рис. 1). Взаимные проводимости могут быть и положительными и отрицательными.

 легко находить любой ток при любых произвольно заданных ЭДС. Например, если в цепи (рис. 1) имеются
легко находить любой ток при любых произвольно заданных ЭДС. Например, если в цепи (рис. 1) имеются  , i1 = 7,188·10-2·10 + 4,375·10-2·20 = 1,595 А
, i1 = 7,188·10-2·10 + 4,375·10-2·20 = 1,595 А . i5 = 0,0313·10 + 0,0630·20 = 1.573 A.
. i5 = 0,0313·10 + 0,0630·20 = 1.573 A. единичную ЭДС
единичную ЭДС  В, действующую по стрелке тока;
В, действующую по стрелке тока; в ветви с источником
в ветви с источником  , а ток в любой ветви
, а ток в любой ветви  (
(  ;
; : eэ = uxx = 8.3 В.
: eэ = uxx = 8.3 В. :
:  А. Отсюда
А. Отсюда Ом.
Ом.
 методом эквивалентного генератора при
методом эквивалентного генератора при 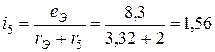 А,
А, и измерять токи
и измерять токи  и
и  ;
; 
 А,
А,  А.
А. Ом,
Ом,  А,
А,  А.
А.
 , тогда
, тогда 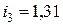 А,
А,  А,
А, .
.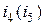 , которая имеет вид
, которая имеет вид  и
и 