 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| СЛОЖНАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА
По теоретическим основам электротехники Линейные электрические Цепи постоянного тока
Новочеркасск 2005
Рецензент канд. техн. наук В.А. Плаксин
Составители: С.Д. Хлебников, И.И. Калинин, Д.Д. Саввин
Лабораторные работы предназначены для студентов II курса энергетических и электротехнических специальностей всех форм обучения, изучающих курс ТОЭ.
© Южно-Российский государственный технический университет, 2005
© Коллектив авторов, 2005 Лабораторная работа № 1
Измерение сопротивления и мощности На постоянном токе Цель работы: ознакомление со способами включения электроизмерительных приборов; выяснение зависимости погрешностей измерения от схемы включения приборов при различных измеряемых сопротивлениях.
Программа работы 1. Произвести измерение сопротивлений методом вольтметра-амперметра двух различных резисторов 2. Теоретически обосновать результат, полученный в п.1 и объяснить, какому сопротивлению точно соответствует приближенная формула 3. Произвести измерения внутренних сопротивлений приборов, использованных в п.1, также методом вольтметра-амперметра. Измерение сопротивления амперметра 4. Теоретически обосновать, что формулы для вычисления сопротивлений 5. Теоретически обосновать, что при известных сопротивлениях измерительных приборов 6. Сравнив приближенные результаты измерений 7. Собрать схему, изображенную на рис. 3, которая с помощью переключателя объединяет обе схемы 1, а и 1, б рис.1. Произвести измерение сопротивления 8. Измерить с помощью ваттметра (рис.4) мощность энергии, потребляемой одним из сопротивлений, выбрав предварительно наиболее рациональные пределы измерений по току и напряжению и рассчитав цену деления ваттметра. Вычислить мощность по формуле Пояснения к работе В данной инструкции вместо обширных словесных пояснений будут приведены числовые расчеты по всем пунктам программы для двух вымышленных резисторов, имеющих сопротивления Для четкого усвоения материала следует прежде всего разобраться с принятыми обозначениями:
принято
При сборке измерительных схем (рис.1 и 2) следует иметь ввиду, что питание осуществляется от источника регулируемого постоянного напряжения; при большом Для сокращения объема работы принято, что допустимы однократные измерения (без статистической обработки многократных измерений с целью уменьшения погрешностей). Разовые измерения должны производиться тщательно. Ниже выполнены расчеты при измерениях по всем пунктам программы. Для лучшей ориентации приводятся точные значения результатов, полученные из этих расчетов:
Показания приборов: IА=0,5 и 1,0 А при измерении «большого» сопротивления по схемам рис. 1а и 1 б; IA= 2,0 и 5,05 А при измерении «малого» сопротивления по схемам рис. 1а и 1 б. UV – показания вольтметра при «измеренных» выше токах.
Рис.1 П.1. Измерение по схеме на рис. 1,а по схеме на рис. 1,б Измерение по схеме 1,à по схеме 1,б В обоих случаях
П.2. В схеме 1,а: IA=Ix в схеме 1,б: UV = UX
Погрешности метода для схемы 1,а: абсолютная относительная Для схемы 1,б: абсолютная относительная Таким образом, по схеме на рис. 1,а сопротивление П.3 и 4. Измерение внутренних сопротивлений амперметра и вольтметра производится по схемам на рис. 2,а и б соответственно. В схеме на рис. 1а вместо реостата можно включать «малое» и «большое» сопротивление.
Рис.2
Для опыта на рис. 2,а: Для опыта на рис. 2,б: При измерениях
П.5. Из П.3 имеем Из П.1 и 2 для схемы 1,а: откуда Для схемы 1,б: gэ=IA/UV =gV+gX, где g=1/r . 1/rx’’=1/rv+1/rx. Откуда т.е.
Таким образом, при учете сопротивлений приборов
П.6.Сравним приближенные и точные результаты измерений для схем на рис.1. Для схемы 1,а: Погрешность для большого сопротивления Для малого сопротивления Для схемы 1,б: при большом сопротивлении
Погрешность для большого сопротивления составляет Для малого сопротивления
Таким образом, на схеме 1,а "большие" сопротивления измеряются с малой погрешностью, а "малые" - с большой. Для схемы 1,б - справедливо обратное утверждение. Понятия "большое" и "малое" сопротивление определяется соотношениями между Таким образом,
П.7.
Вычисляют мощности
Сопротивление Для
Сопротивление
П.8. Для непосредственного измерения мощности служит ваттметр. На рис. 4 показаны различные способы изображения ваттметра на схемах электрических цепей. У ваттметра имеются токовая обмотка (зажимы *I - I) и обмотки напряжения (зажимы *U - U) (звездочками маркированы одноименные зажимы "начала" обмоток). Токовая обмотка ваттметра, подобно амперметру, включается последовательно с цепью, в которой производится измерение мощности. Обмотка напряжения подобно вольтметру включается параллельно с указанной цепью. Поэтому утрированно можно представить, что ваттметр - это как бы амперметр с сопротивлением riw и вольтметр с сопротивлением ruw в одном корпусе, при измерении мощности в "большом" и "малом" сопротивлениях. Схемы включения обмоток такие же, как для вольтметра и амперметра (рис. 5). Заменим сопротивления обмоток ваттметра резисторами. Тогда получим схему рис. 6. (Сравните схемы на рис. 5 и 6 со схемами рис. 1а и 1б).
Рис. 4
Рис.5
Рис.6.
Цена деления ваттметра
Например: в шкале 150 делений; В лаборатории необходимо по схеме цепи рис.4 измерить показания ваттметра Pw и амперметра
Лабораторная работа N 2 СЛОЖНАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА
Цель работы - освоение и экспериментальное подтверждение законов Кирхгофа для цепей постоянного тока. Программа работы 1. Для электрической цепи (схема на рис. 1, вариант задается преподавателем) с известными параметрами расставить стрелки токов, составить систему уравнений Кирхгофа и на персональном компьютере(ПК) рассчитать токораспределение.
Рис. 1 Величины, полярностьЭДСи места ихвключения задаются преподавателем, величины сопротивлений указаны на стенде. 2. Записать уравнения по первому закону Кирхгофа в формулировке 3. Записать уравнение по второму закону Кирхгофа для какого-либо контура цепи в формулировке 4. Приняв потенциал какой-либо точки контура из п.З равным нулю, измерить потенциалы всех доступных точек контура. Вычислить напряжения между различными точками контура, используя потенциалы, и сравнить с измерениями напряжений в п.З.Построитьпотенциальную диаграмму для выбранного контура. 5. Записать уравнение по второму закону Кирхгофа для другого контура в формулировке 6. Используя второй закон Кирхгофа в формулировке п. 5, вычислить напряжение между какими-либо точками а и Ь контура, указав стрелкой направление вычисления. Непосредственным измерением этого напряжения подтвердить вычисление. Описание стенда Сложная цепь, содержащая не более 6 ветвей и не более 2 источников постоянного напряжения, собирается по мнемосхеме, изображенной на лицевой панели съемного стенда, путем включения штеккерных перемычек и проводов (рис. 1). Регулируемый источник питания (0 - 127 В) представляет собой выпрямительную установку с ЛАТРом и сглаживающим фильтром. Чтобы такой источник можно было считать идеальным ( В данной работе источники должны быть электрически независимы, что в лаборатории 301 обеспечено только для стендов N 7-8, 9-10; на других столах выполнять эту лабораторную работу недопустимо.
Рис. 2 Измерение токов и напряжений производится амперметром и вольтметром магнитоэлектрической системы (МЭ). Эти приборы фиксируют не только величину, но и знак (+, -). Включение приборов при заранее выбранных направлениях (стрелках) тока, напряжения, ЭДС показано на рис. 2. Если приэтом стрелка прибора зашкаливает влево, то полярность следует изменить, а показание прибора записатьсо знаком "минус". Измерение потенциала Пояснения к выполнению Пояснения даны в виде числовых расчетов для цепи, конфигурация и параметры которой отличаются от исследуемой на стенде. Ниже приводятся расчеты и "измерения" по всем пунктам программы, а также необходимые комментарии. Числа в примере подобраны так, что вычисления легко выполняются вручную.
П. 1. На рис. 3 приведена схема цепи с указанием направлений вычисления и "измерения" токов и напряжений (стрелки токов и напряжений), узлы и контуры пронумерованы. Числовые значения параметров цепи:
Расчетная система уравнений Кирхгофа для токов (узлы 3 и 4 объединены, ток 1) 2) контурные уравнения 11) 22) 33) Уравнения в матричной форме и с учетом числовых значений:
Решение на ПК дает
Примечание: Между узлами 3 и 4 находится "пустая" ветвь (r=0); при расчете токораспределения она исключена, ток П. 2. Для узла 2:
Рис. 3 “Измерения” (в примере - условно) с помощью амперметра магнитоэлектрическойсистемы дали: i1=1,6 А, i2 =0,6 А, i3 =2,2 А, i4 =-0,62 А, i5 =1,55А. Подстановка чисел в (1) дает: -2,2-(-0,62)+1,55=0,
Равенство (1) удовлетворяется с относительной погрешностью
Для сечения (2): -1,6-0,6-(-0,62 )+1,55=0; 2,17 Если считать точность измерений удовлетворительной, то принцип непрерывности тока Примечание. Будем считать, что алгебраические равенства для «измеренных» токов и напряжений выполняются, если невязка не превышает 5% от суммарной величины всех положительных (или отрицательных) членов «измеренных» токов либо напряжений (и определяются точностью измерений и погрешностью приборов). П.З. Для контура 22 на рис. 3:
Измерения напряжений с помощью вольтметра МЭ системы дали (условно); ue3=20 В, ur3=10,5 В, ur4= -3 В, ur2=6 В при подстановке в (3), получим -20+10,5-(-3)+6=0, т.е. -20
П. 4. Измерение потенциалов. Примем
Принцип потенциальности здесь должен выполняться автоматически, так как
Однако, из-за погрешностей измерения невязка в сумме напряжений составит 6-20+10,5+3=0,5 В (2,5 %). На рис. 4 приведена потенциальная диаграмма, построенная для замкнутого контура 3-1-в-2-3. По оси абсцисс отложены сопротивления (Ом) участков цепи, по оси ординат - потенциалы отмеченных точек контура. На диаграмме показаны наибольшее иmax и наименьшее иmin напряжения между доступными точками контура. Наибольшее напряжение особенно важно при изготовлении стендов и печатных плат. Точки с максимальным напряжением не должны располагаться близко друг к другу, чтобы не произошел электрический пробой.
Рис. 4 П. 5. В формулировке Для контура 11 на рис. 3:
При измеренных (условно) напряжениях
справедливость контурного уравнения Кирхгофа подтверждается.
П.6. Для вычисления напряжения иab контур аb1а (рис. 3):
откуда С другой стороны, Пояснения к п.6. Произвольно расположенные точки (а, b) соединены в цепи различными проводящими путями (например, через ветви 1 и 3, либо 1, 4 и 3, либо 1, 5 и 3). При вычислении иab можно выбрать любой путь, т.к. напряжение от него не зависит (принцип потенциальности). Цепь вольтметра соответствует стрелке напряжения иab; при Заметим, что при компьютерных расчетах неопределенность
Лабораторная работа N 2,А |



 и
и  по каждой из возможных схем включения приборов (рис.1, а и б). Убедиться, что вычисленные значения
по каждой из возможных схем включения приборов (рис.1, а и б). Убедиться, что вычисленные значения  без учета сопротивлений приборов не одинаковы для одного и того же резистора (
без учета сопротивлений приборов не одинаковы для одного и того же резистора (  ) и зависят от измерительной схемы (через
) и зависят от измерительной схемы (через  обозначено измерение по схеме 1,а;
обозначено измерение по схеме 1,а;  - по схеме 1,б ).
- по схеме 1,б ). для обеих измерительных схем рис.1. Вывести формулы погрешностей метода измерения.
для обеих измерительных схем рис.1. Вывести формулы погрешностей метода измерения. выполнить по схеме на рис. 2,а ; сопротивление вольтметра
выполнить по схеме на рис. 2,а ; сопротивление вольтметра  - по схеме на рис. 2,б.
- по схеме на рис. 2,б. по показаниям приборов в схемах на рис. 2 являются точными, т.е. не содержат погрешностей метода измерения.
по показаниям приборов в схемах на рис. 2 являются точными, т.е. не содержат погрешностей метода измерения. и
и  и
и  (из п.1) и
(из п.1) и  и сравнить с измеренной ваттметром.
и сравнить с измеренной ваттметром. - точное значение сопротивления, вычисленное по точным значениям напряжения
- точное значение сопротивления, вычисленное по точным значениям напряжения  и тока
и тока  для резистора
для резистора  , поэтому
, поэтому  - сопротивление амперметра и вольтметра;
- сопротивление амперметра и вольтметра; - показания амперметра и вольтметра;
- показания амперметра и вольтметра;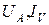 - напряжение на амперметре и ток вольтметра (измеряются в схемах на рис. 2а и б);
- напряжение на амперметре и ток вольтметра (измеряются в схемах на рис. 2а и б); - приближенное значение сопротивления
- приближенное значение сопротивления  , вычисленное по измерениям в схеме на рис.1,а;
, вычисленное по измерениям в схеме на рис.1,а;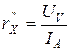 - приближенное значение
- приближенное значение 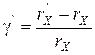 - относительная погрешность для схемы на рис. 1,a;
- относительная погрешность для схемы на рис. 1,a; - то же для схемы на рис. 1,б;
- то же для схемы на рис. 1,б; - критическое сопротивление, при котором
- критическое сопротивление, при котором  .
. , а при малом сопротивлении
, а при малом сопротивлении  .
. Ом;
Ом; 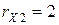 Ом;
Ом; 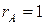 Ом;
Ом;  Ом;
Ом; Ом.
Ом.

 Ом;
Ом; Ом.
Ом. Ом;
Ом;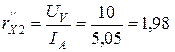 Ом.
Ом. .
.


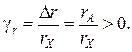


 всегда измеряется с избытком
всегда измеряется с избытком  , а по схеме на рис.1,б - с недостатком
, а по схеме на рис.1,б - с недостатком  .
.

 А,
А,  В,
В,  Ом.
Ом. А,
А,  В,
В,  Ом.
Ом.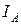 ,а вольтметр показывает точное значение напряжения на амперметре UV; в схеме 2,б показание вольтметра точно соответствует напряжению
,а вольтметр показывает точное значение напряжения на амперметре UV; в схеме 2,б показание вольтметра точно соответствует напряжению  и амперметр показывает точное значение тока вольтметра, равное IA.
и амперметр показывает точное значение тока вольтметра, равное IA. Ом,
Ом,  Ом.
Ом. ,
, Ом,
Ом,  Ом.
Ом.
 Ом,
Ом,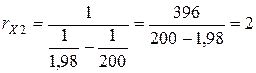 Ом.
Ом. Ом,
Ом,  Ом.
Ом. , т.е. составляет 1%.
, т.е. составляет 1%. имеем
имеем  Ом,
Ом,  , т.е. составляет 50%.
, т.е. составляет 50%.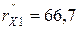 Ом,
Ом, 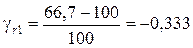 , т.е. составляет 33,3%.
, т.е. составляет 33,3%.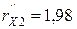 Ом,
Ом,  , т.е. составляет 1%.
, т.е. составляет 1%.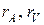 . Существует такое
. Существует такое  . Можно показать, что
. Можно показать, что  принято называть "большим" сопротивлением и применять измерительную схему 1,а; сопротивление
принято называть "большим" сопротивлением и применять измерительную схему 1,а; сопротивление  принято называть "малым" и применять измерительную схему 1,б. В рассматриваемом примере
принято называть "малым" и применять измерительную схему 1,б. В рассматриваемом примере  Ом.
Ом. Ом >
Ом >  Ом - "большое" сопротивление, а
Ом - "большое" сопротивление, а  Рис.3
Рис.3 при положениях переключателя а и б и неизменном входном напряжении.
при положениях переключателя а и б и неизменном входном напряжении. и сравнивают их; цепь, для которой мощность окажется меньшей, дает меньшую погрешность измерения
и сравнивают их; цепь, для которой мощность окажется меньшей, дает меньшую погрешность измерения  В получим:
В получим: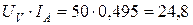 Вт (положение переключателя а);
Вт (положение переключателя а); Вт (положение переключателя б).
Вт (положение переключателя б). Ом.
Ом. В будет:
В будет: Вт - (положение переключателя а);
Вт - (положение переключателя а); Вт- (положение переключателя б).
Вт- (положение переключателя б). Ом.
Ом.




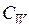 (Вт/дел) рассчитывается как
(Вт/дел) рассчитывается как
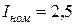 А;
А;  В,
В, Вт/дел.
Вт/дел. (для выбора предела ваттметра по напряжению в схемах на рис.4 включен вольтметр). Сравнить показание ваттметра с мощностью, вычисленной по формуле
(для выбора предела ваттметра по напряжению в схемах на рис.4 включен вольтметр). Сравнить показание ваттметра с мощностью, вычисленной по формуле  и сделать выводы.
и сделать выводы.

 для какого-либо узла и какого-либо сечения цепи. Измерить токи, входящие в эти уравнения, и убедиться в справедливости принципа непрерывности электрического тока.
для какого-либо узла и какого-либо сечения цепи. Измерить токи, входящие в эти уравнения, и убедиться в справедливости принципа непрерывности электрического тока. Измерить напряжения на всех элементах цепи (uek - на "источниках",
Измерить напряжения на всех элементах цепи (uek - на "источниках",  - на "приемниках") и убедиться в справедливости принципа потенциальности.
- на "приемниках") и убедиться в справедливости принципа потенциальности. . Измерить все величины, входящие вэто уравнение, и убедиться в его справедливости.
. Измерить все величины, входящие вэто уравнение, и убедиться в его справедливости.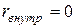 ), необходимо поддерживать неизменное, заданное заранее, напряжение при любом (допустимом!) токе. Это выполняют вручную с помощью ЛАТРа при каждом изменении режима (токов в цепи).
), необходимо поддерживать неизменное, заданное заранее, напряжение при любом (допустимом!) токе. Это выполняют вручную с помощью ЛАТРа при каждом изменении режима (токов в цепи).

 произвольной точки а - это измерение напряжения
произвольной точки а - это измерение напряжения  , где о - заранее выбранная точка "нулевого потенциала".
, где о - заранее выбранная точка "нулевого потенциала". В,
В,  В,
В,  Ом,
Ом, 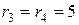 Ом,
Ом,  Ом
Ом исключен)
исключен)
 ;
; ,
, ,
, .
.

 А,
А,  А,
А,  А,
А, А,
А,  А,
А,  А.
А. (1). Для сечения, обозначенного штриховой линией (рис.3):
(1). Для сечения, обозначенного штриховой линией (рис.3):  (2).
(2).
 .
.
 2,2.
2,2. - подтверждается.
- подтверждается. (3)
(3)
 . Тогда
. Тогда B,
B,  B,
B,  B,
B,  В.
В.


 В,
В,  В,
В, 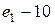 В; -16+6= -10,
В; -16+6= -10, ,
, В.
В. .
. ток вольтметра
ток вольтметра  , т.е. эта ветвь - ветвь с разрывом. Напряжение иab не может вычисляться через параметры этой ветви, т.к. иab=ivrv=0
, т.е. эта ветвь - ветвь с разрывом. Напряжение иab не может вычисляться через параметры этой ветви, т.к. иab=ivrv=0  - неопределенность. Однако, указав стрелкой направление измерения (вычисления) напряжения на разрыве а - b, мы получим "замкнутый" контур, т.к. остальная его часть проходит через проводящие ветви цепи (возможные пути перечислены в начале пояснений).
- неопределенность. Однако, указав стрелкой направление измерения (вычисления) напряжения на разрыве а - b, мы получим "замкнутый" контур, т.к. остальная его часть проходит через проводящие ветви цепи (возможные пути перечислены в начале пояснений). можно устранять простым приемом, полагая что rv не бесконечно велико, а превышает сопротивления всех других элементов цепи на несколько порядков (103 -106). Тогда
можно устранять простым приемом, полагая что rv не бесконечно велико, а превышает сопротивления всех других элементов цепи на несколько порядков (103 -106). Тогда  , а будет много меньше всех других токов (в 103-106 раз), и напряжение иab определяется однозначно по равенству иab=ivrv. Такой прием соответствует физике явлений и точности практических измерений.
, а будет много меньше всех других токов (в 103-106 раз), и напряжение иab определяется однозначно по равенству иab=ivrv. Такой прием соответствует физике явлений и точности практических измерений.