 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проверка различия средних арифметических
Обычно при сравнении существующего технологического процесса с усовершенствованным технологическим процессом, при сравнении производственной методики по способу А и В, при сопоставлении результатов работы группы А и группы В и т.д. среднее генеральной совокупности часто бывает неизвестно. В такого рода ситуациях рекомендуется осуществлять проверку, придерживаясь следующего порядка. Прежде всего, определяют отношение дисперсий, полученных из несмещенных оценок sе12, sе22 для двух групп выборок, и осуществляют проверку по F-распределению, в результате чего убеждаются, что в дисперсии не обнаруживается существенного различия. В том случае, когда между sе12 и sе22 имеется существенное различие, то определить общую дисперсию s22 становится невозможным. Если нет существенного различия между sе12 и sе22, то обозначая средние арифметические измеренных значений двух групп выборок n1, n2 через
При проверке существенного различия средних арифметических в двух группах выборок целесообразно применить формулу:
и осуществлять проверку по t-распределению. При этом число степеней свободы равно Ф = n1+n2 - 2. Объединив вместе все процедуры проверки при данной ситуации, получают: 1. Н0:s12 = s22, а также m1 = m2. 2. Определяют дисперсии sе12, sе22 и осуществляют проверку по F-критерию. Если нет существенного различия переходят к следую- щему процессу. 3. Н1:m1 ¹ m2. 4. Определив sе2, вычисляют t0. 5. Сравнив t0 со значениями tф,a из таблицы t-распределения при Ф = n1+n2 - 2, делают выводы.
Пример 3.4. Проверить, существенно ли различие в средних значениях твердости после закалки, произведенной на устройствах А и В, пользуясь данными примера 3.3. Решение: 1. Н0:sА2 = sВ2, mА = mВ. 2. В результате проверки по F-критерию, как уже было описано выше, существенного различия не было установлено. 3. Н1:mА ¹ mВ. 4. Определяют несмещенную оценку дисперсии по зависимости (2.6):
5. Вычисляют по выражению (3.7) t0:
6. Выносится решение: t9;0.01 = 3.25 > t0. Существенного различия между средними значениями не установлено.
Статистическое оценивание количественных значений. Интервальная оценка. 3.4.1. Ситуация, когда дисперсия генеральной совокупности s2 уже известна
Если определить среднее арифметическое в выборке объемом n, взятой методом случайного отбора образцов из нормальной генеральной совокупности со средним арифметическим m и дисперсией s2 и нормировать его, то выражение (3.1) подчинится нормальному распределению со средним значением m = 0 и дисперсией s2 = 1. Приняв значение U, соответствующее уровню значимости a, за Ua , получают, что вероятность неравенства
будет (1- a). Видоизменив эту формулу, получают нижнюю границу Пример 3.5. Известно, что среднее арифметическое отклонение массы изделий, изготовленных неким технологическим процессом, составляет s =3,5 г. Далее в результате измерения массы этих изделий в выборке объемом n=4, извлеченной случайным отбором, было получено Решение. Поскольку 1 - a = 0,99, то a = 0,01. По табл.1 Приложения находим U0,01 = 2,576. Нижняя граница Верхняя граница Таким образом, среднее арифметическое генеральной совокупности находится в интервале 58,3 < m < 72,5 г.
3.4.2. Ситуация, когда дисперсия генеральной совокупности s2 неизвестна Если дисперсия генеральной совокупности s2 неизвестна и при этом использовать выражение (2.10), то определенное при помощи выражения (3.2) распределение статистической величины t принимает распределение Стьюдента при числе степеней свободы Ф = n - 1. Доверительный интервал, обусловленный вероятностью (1 - a), выражают:
причем доверительные границы
Пример 3.6. Для того, чтобы узнать величину поводки, полученную при термообработке штампованных деталей, была взята выборка n = 10 и получены Необходимо определить границы 95%-ного доверительного интервала для величины поводки этих деталей. Решение.
Доверительные границы
Доверительный интервал 0,054 мм - 0,116 мм.
|



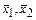 , а сумму квадратов через S1, S2, можно построить предположение, что дисперсия генеральной совокупности s2 оценивается общей для двух групп несмещенной оценкой
, а сумму квадратов через S1, S2, можно построить предположение, что дисперсия генеральной совокупности s2 оценивается общей для двух групп несмещенной оценкой  :
: =
= 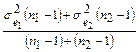 (3.6)
(3.6) (3.7)
(3.7)


 <
<  <
<  (3.8)
(3.8) и верхнюю границу
и верхнюю границу  нахождения среднего арифметического m. Это и есть доверительный интервал.
нахождения среднего арифметического m. Это и есть доверительный интервал. г. Предлагается сделать интервальную оценку среднего арифметического для массы в генеральной совокупности при доверительной вероятности 99%.
г. Предлагается сделать интервальную оценку среднего арифметического для массы в генеральной совокупности при доверительной вероятности 99%. г.
г. г.
г.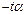 <
<  <
<  (3.9)
(3.9) (3.10)
(3.10) = 0,085 мм, sе = 0,042 мм.
= 0,085 мм, sе = 0,042 мм.
