 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Количественные характеристики распределения
ПОСТРОЕНИЕ ГИСТОГРАММЫ, РАСЧЕТ КОЛИЧЕСТВЕННЫХ ХАРАКТЕРИСТИК, ПРОВЕРКА ГИПОТЕЗЫ НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ Плотность распределения. Гистограмма
Одним из способов графического изображения плотности распределения является гистограмма (столбиковая диаграмма). Это такой вид диаграммы, который при помощи столбиков, расставленных в ряд на мелких размерных интервалах, отражает состояние качества проверенной партии изделий и помогает разобраться в состоянии измерений или качества изделий в генеральной совокупности, выявить в ней положение среднего значения и характер рассеивания.
Построение гистограммы
Рассматривая таблицу 2.1, можно понять, что одним зрительным восприятием этих данных невозможно получить достоверную информацию о состоянии качества изделий в генеральной совокупности (например, в партии изделий). Отсюда следует, что эти данные необходимо упорядочить. В такой ситуации лучше всего составлять гистограмму.
Таблица 2.1 Коэффициенты деформации деталей в процессе термообработки
При составлении гистограммы (рис.2.1) рекомендуется придерживаться следующего порядка: 1) среди измеренных значений находят максимальное Xmax и минимальное Xmin значения и определяют широту распределения по формуле R = Xma x - Xmin. В данном случае R =1,8 - 0,1 = 1,7; 2) определяют количество интервалов (классов) 3) делят широту распределения R на количество интервалов к, полученный результат округляют и принимают за широту интервала h = R/k = 1,7/10 = 0,17 » 0,2; 4) размечают в бланке регистрации (табл.2.2) интервалы варьирования, устанавливая граничные значения с конца одной из сторон, а также вписывают значения середины интервалов;
Таблица 2.2
5) просматривают таблицу 2.1 по порядку от первой до последней строчки и при чтении каждого результата соответствующую метку (черточку) заносят в тот класс, к которому относится данное наблюдение. Каждый знак 6) по оси абсцисс наносят границы интервалов, а по оси ординат шкалу для частот. Над интервалами вычерчивают прямоугольники, высота которых пропорциональна частотам.
Количественные характеристики распределения 2.3.1. Среднее арифметическое
Предположим, что в результате измерений получены величины х1, х2, х3, . . . , хn, число которых равно n. Тогда среднее арифметическое
или В тех случаях, когда измеряемые величины разделяют на интервалы, то, обозначив значения середины каждого интервала через хj=х1, х2, х3,…, хк, а частоту в этих интервалах соответственно через fj = f1, f2 , …., fk , среднее арифметическое
В сокращенном виде формула будет иметь вид:
2.3.2. Рассеивание значений
Для количественной оценки рассеивания значений часто используют сумму квадратов отклонений, дисперсию, среднее квадратическое отклонение. Сумма квадратов отклонений S Отклонением называют разницу между каждым измеренным значением величины и ее средним арифметическим (хi -
Дисперсия sе2 Если сумма квадратов отклонений S выражает рассеивание значений во всем комплексе данных, то дисперсия sе2, полученная делением S на число n -1 данных, является мерой рассеивания на каждую отдельную единицу данных:
Среднее квадратическое отклонение sе Взятый с положительным знаком квадратный корень из дисперсии называют средним квадратическим отклонением sе:
Нормальное распределение
При большом числе данных соответственное сужение интервалов в распределении влечет за собой постепенное приближение гистограммы к гладкой кривой. Если же число данных будет беспредельно большое, то гистограмма превратится в безукоризненную кривую. В этом случае кривая может рассматриваться в качестве распределения генеральной совокупности (рис. 2.2). Если кривая распределения имеет тенденцию в центре обнаруживать один пик, причем симметрично справа и слева от среднего арифметического она принимает форму колокола, то такую кривую называют нормальным распределением, или распределением Гаусса. Закон, или функцию нормального распределения выражают следующей формулой:
где m - среднее арифметическое распределения; s - среднее квадратическое отклонение. Величины m и s называют параметрами распределения. Для удобства вычисления функции распределения y = f (x) случайные величины нормируют по формуле:
Нормальное распределение с параметрами m = 0 и s =1 называется нормированным нормальным распределением (рис.2.3.). Функция нормального нормированного распределения примет вид:
При анализе качества продукции количество замеров не всегда бывает достаточным для определения законов распределения. Но если заранее известен закон распределения, то для определения важнейших числовых характеристик распределения нужно небольшое количество замеров. В том случае, когда закон распределения случайной величины близок к нормальному, для обработки результатов опытов необходимо определение двух статистических оценок параметров распределения:
|



 , где n - число наблюдений;
, где n - число наблюдений;

 Частота
Частота определяют по следующей формуле:
определяют по следующей формуле:
 (2.1)
(2.1)
 (2.2)
(2.2)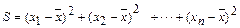
 (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) , (2.6)
, (2.6) .
.

 (2.7)
(2.7)