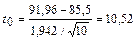ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проверка гипотезы нормальности распределения
Некоторое представление о близости эмпирического распределения к нормальному дает анализ показателей асимметрии и эксцесса. Показатель асимметрии определяют по формуле:
где третий центральный момент;
среднее квадратическое отклонение. Показатель эксцесса определяют по формуле:
где четвертый центральный момент. Для симметричных распределений m3 = 0, m4/se4 = 3, следовательно, А = 0 и Э = 0. Несмещенные оценки для показателей асимметрии и эксцесса находят по формулам:
Для проверки гипотезы нормальности распределения следует также вычислить среднеквадратические отклонения для показателей асимметрии и эксцесса:
Если выполняются условия
Пример выполнения проверки гипотезы Нормальности распределения
Используя данные табл.2.2 определить количественные характеристики распределения и проверить гипотезу о нормальности распределения. По формулам (2.2), (2.4), (2.8), (2.11), (2.13), (2.14), (2.15) и (2.16) находим следующие значения:
следовательно, данное распределение можно отнести к нормальному. С целью упрощения необходимые для расчета данные сводим в таблицу (табл.2.3).
Вариант задания Для определения варианта задания из табл. 2.1 выписывают все столбики и строки, за исключением тех столбиков и строк, порядковые номера которых совпадают, соответственно с последней и предпоследней цифрами номера зачетной книжки.
Таблица 2.3 Вычисление количественных характеристик
ЗАДАНИЕ 3
СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ И ПРОВЕРКА КОЛИЧЕСТВЕННЫХ ОЦЕНОК
Выбор правильного решения из двух противоположных предположений о генеральной совокупности называется статистической проверкой. Предположительная количественная оценка параметра генеральной совокупности называется статистическим оцениванием.
Проверка средних значений
3.1.1. Ситуация, когда среднее арифметическое по совокупности m и дисперсия генеральной совокупности s2 известны
В практической деятельности ситуация, когда m и s2 генеральной совокупности уже известны, встречаются редко. Однако, такую ситуацию можно приближенно заменить ситуацией, при которой из многочисленных данных статистически управляемого технологического процесса можно определить среднее арифметическое и дисперсию. Ниже рассмотрим ситуацию, когда проверяют, действительно ли n-ное количество данных, которые считаются взятыми из генеральной совокупности, имеющей нормальное распределение, взяты из этой генеральной совокупности. Порядок проверки гипотез: 1. Строят нулевую гипотезу (ее обозначают H0). H0 : m1 = m2 (n-е количество данных взято из идентичной генеральной совокупности, имеющей нормальное распределение). 2. Выдвигают альтернативную гипотезу: Н1: m1 ¹ m2 (n-е количество данных было взято не из идентичной генеральной совокупности). 3. Выбирают тип распределения, исходя из гипотезы 1 принимают нормальное распределение N(m, s2). 4. Вычисляют статистическую оценку
5. Принимают решение о проведении двухсторонней либо односторонней проверки гипотез. Разграничение области 5%, 1%-ного уровня значимости и т.д. называют областями отклонения гипотезы. На рис. 2.1 они заштрихованы. Эти области отклонения иногда берут по обе стороны распределения, а иногда по одну сторону. Например, в отличие от нулевой гипотезы m1 =m2, если предположить, что альтернативная гипотеза будет m1 ¹ m2, то область отклонения берут с двух сторон, если же предположить, что она m1 > m2 или m1 < m2, то берут только с одной стороны. Такие проверки гипотез соответственно называют двухсторонней или односторонней проверкой. 6. Принимают решение отклонить или принять нулевую гипотезу. После того, как в табл.1 Приложения будут найдены числовые значения величин, соответствующие 5% или 1%-ному уровню значимости, их сравнивают со статистическими оценками, полученными в результате вычислений, и выносится решение.
Если расхождения нулевая значение ® не являются ® гипотеза U0 < Ua значимыми принимается
Если расхождения альтернативная значение ® являются ® гипотеза U0,01 > U0 > U0.05 значимыми принимается
Если расхождения альтернативная значение ® имеют высокую ® гипотеза U0 > U0.01 степень значи- принимается мости
Пример 3.1. Выход годной продукции в технологическом процессе составлял: среднее арифметическое m =85,5%, среднее квадратическое отклонение s =4,5%. После внесения в технологический процесс усовершенствований, собранные в течение четырех дней данные составили `х = 93,3%.
Рис.3.1 Распределение и уровень значимости
Можно ли утверждать, что между первым и вторым случаем имеется расхождение? Решение: 1. Н0 : m1 = m2 2. Н1 : m1 ¹ m2 (двухсторонняя оценка). 3. Среднее 4. По формуле (3.1)
5. При сравнении с 1%-ным уровнем значимости получится U0 =3,42 > U0.01 = 2,58. Следовательно, расхождение имеет высокую степень значимости. Значения Ua , берут из табл.1 Приложения.
3.1.2. Ситуация, когда известно только среднее арифметическое генеральной совокупности m
Поскольку дисперсия генеральной совокупности s2 неизвестна, необходимо пользоваться ее предположительной оценкой, исходя из выборочных данных. А именно, осуществляют проверку над m, используя 1. Строят нулевую гипотезу: Н0:m1 = m2. 2. Строят альтернативную гипотезу: Н1:m1 ¹ m2 (двухсторонняя проверка), m1 > m2 или m1 < m2 (односторонняя проверка). 3. Выбирают распределение для проверки статистических оценок. Поскольку s неизвестно, проводят проверку, используя sе и основываясь на t-распределении. 3. Вычисляют статистические оценки
5. Сравнивая значение из таблицы t-распределения (для соответствующей степени свободы Ф = n -1 и уровня значимости a) и значение t0, принимают решение. Если t0 > t(Ф; 0.05) , то различие имеет место, поскольку уровень значимости 5%-ный. Если t0 > t(Ф; 0.01) , то имеет место существенное различие, поскольку уровень значимости 1%-ный.
Пример 3.2. До сих пор выход годной продукции в технологическом процессе в среднем составлял 85,5%. После того, как технологический процесс был усовершенствован, данные, собранные за 10-дневный срок, позволили получить следующие цифровые значения:
Можно ли утверждать, что выход годной продукции увеличился? Решение: 1. Н0:m1 = m2 2. Н1:m1 < m2 (односторонняя проверка). 3. Определяют среднее арифметическое выборки
Определяют сумму квадратов S по зависимости (2.3):
Определяют среднее квадратическое отклонение sе (2.10):
4. Определяют t0 по формуле (3.2):
5. Сравнивают со значениями из таблицы t-распределения. Эта проверка является односторонней, поскольку проверяется: "Можно ли утверждать, что объем выхода годного увеличился?". По табл.2 Приложения определяют tФ,a = tg9;0.02 = 2,821.Так как t0 = 10,52 > tФ,a = 2,821, то можно утверждать, что выход годного существенно увеличился.
|



 (2.8)
(2.8) - (2.9)
- (2.9)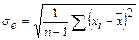 - (2.10)
- (2.10) (2.11)
(2.11) - (2.12)
- (2.12) (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) (2.16)
(2.16) и
и  , то гипотезу нормальности исследуемого распределения принимают.
, то гипотезу нормальности исследуемого распределения принимают.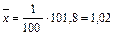






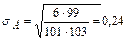


 ,
,




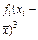

 (3.1)
(3.1)


 при n = 4 подчиняется нормальному распределению.
при n = 4 подчиняется нормальному распределению.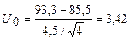 .
.
 и основываясь на t-распределении (Стьюдента):
и основываясь на t-распределении (Стьюдента): . (3.2)
. (3.2)