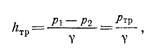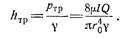ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ТЕОРИЯ ЛАМИНАРНОГО ТЕЧЕНИЯ ЖИДКОСТИ В КРУГЛОЙ ТРУБЕ
Ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости; оно подчиняется закону трения Ньютона и вполне определяется этим законом. Поэтому теория ламинарного течения жидкости основывается на законе трения Ньютона.
Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d=2r. Чтобы исключить влияние силы тяжести и этим упростить вывод, воспользуемся трубой, расположенной горизонтально. Достаточно далеко от входа в нее выделим отрезок потока длиной l между сечениями 1—1 и 2—2 (рис. 45). Пусть в первом сечении давление равно p1, а во втором p2. Ввиду постоянства диаметра трубы скорость и коэффициент a будут неизменными вдоль потока, поэтому уравнение Бернулли для выбранных сечений примет вид
где hтр—потеря напора на трение. Отсюда
что и показывают пьезометры, установленные в сечениях. В потоке жидкости выделим цилиндрический объем радиуса r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т. е. равенство нулю суммы двух сил, действующих на объем: силы давления и силы сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через t, получим
откуда
Из формулы видно, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на том же рис. 45 слева. Значение скорости на окружности радиуса r таково:
Это есть закон распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, оказывается параболой второй степени. Максимальная скорость в центре сечения (при r=0) равна
Входящее в формулу (6. 1) отношение ртр/l, как видно из рис. 45, представляет собой гидравлический (пьезометрический) уклон, умноженный на g. Эта величина является постоянной вдоль прямой трубы постоянного диаметра. Для расхода будем иметь:
Найдем среднюю по сечению скорость делением расхода на площадь:
.Сравнивая это выражение с формулой (6.2), приходим к выводу, что средняя скорость при ламинарном течении в два раза меньше максимальной, т. е.
Для получения закона сопротивления, т. е. выражения потери напора на трение hтр через расход и размеры трубы, определим ртр из формулы (6. 3):
Разделив уравнение на g, получим потерю напора:
Заменяя m через nr и g через gr, а также переходя от r0 к d=2r0, окончательно получим
Полученный закон сопротивления показывает, что при ламинарном течении в круглой трубе потеря напора на трение пропорциональна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуазейля — Гагена, используется для расчета трубопроводов с ламинарным режимом течения. Закон сопротивления:
где
Индекс «л» при l поставлен для того, чтобы подчеркнуть, что здесь речь идет о ламинарном течении. Следует иметь в виду, что потеря напора на трение при ламинарном течении пропорциональна скорости в первой степени. Коэффициент a, учитывающий неравномерность распределения скоростей в уравнении Бернулли, для случая стабилизированного ламинарного течения жидкости в круглой трубе: a = 2. Итак, истинная кинетическая энергия ламинарного потока с параболическим распределением скоростей в два раза превосходит кинетическую энергию того же потока, но при равномерном распределении скоростей. Таким же образом, можно показать, что секундное количество движения ламинарного потока с параболическим распределением скоростей в b раз больше количества движения того же потока, но при равномерном распределении скоростей, причем коэффициент равен постоянной величине:
Изложенная теория ламинарного течения жидкости в круглой трубе в общем хорошо подтверждается опытом, и выведенные законы сопротивления и распределения скоростей обычно не нуждаются в каких-либо поправках, за исключением следующих случаев. 1. При течении в начальном участке трубы, где происходит постепенное установление параболического профиля скоростей. Сопротивление на этом участке получается больше, чем на последующих участках трубы. Однако это обстоятельство учитывают лишь при расчете очень коротких труб. 2. При течении со значительным теплообменом, т. е. в том случае, когда движение жидкости сопровождается ее нагреванием или охлаждением. 3. При очень высоких перепадах давления. |