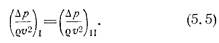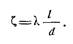ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ТРУБАХ
РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ТРУБАХ. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ
Опыты показывают, что возможны два режима или два вида течения жидкостей (а также газов) в трубах: ламинарное и турбулентное Ламинарное течение — это слоистое течение без перемешивания частиц жидкости и без пульсаций скорости. При таком течении все линии тока вполне определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т. е. прямолинейны; отсутствуют поперечные перемещения частиц жидкости, а потому не происходит перемешивания жидкости в процессе ее течения Пьезометр, присоединенный к трубе с установившимся ламинарным течением, показывает неизменность давления (и скорости) по времени, отсутствие колебаний (пульсаций). Таким образом, ламинарное течение является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и неустановившимся) Однако ламинарное течение нельзя считать безвихревым, так как в нем хотя и нет ярко выраженных вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с вполне определенными угловыми скоростями. Турбулентное течение — это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении линии тока лишь примерно определяются формой русла. Движение отдельных частиц оказывается неупорядоченным, траектории подчас имеют вид замысловатых кривых. Объясняется это тем, что при турбулентном течении наряду с основным продольным перемещением жидкости вдоль русла имеют место поперечные перемещения и вращательное движение отдельных объемов жидкости. Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости и обратно пропорционально диаметру трубы, т. е.
Оказывается, что входящий сюда безразмерный коэффициент пропорциональности k имеет универсальное значение, т. е. одинаков для всех жидкостей и газов и любых диаметров труб. Это означает, что смена режима течения происходит при вполне определенном соотношении между скоростью, диаметром и вязкостью, равном
Это безразмерное число называется критическим числом Pейнольдса по имени английского ученого, который установил этот критерий, и обозначается
Как показывают опыты, критическое число Рейнольдса приблизительно равно 2300. Однако можно говорить не только о критическом числе Reкр, соответствующем смене режима, но и о фактическом числе Рейнольдса для того или иного потока и выражать его через фактическую скорость, т. е.
Таким образом, мы получаем критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе<Rекр течение оказывается ламинарным; при Rе>Rекр течение обычно турбулентное. Зная скорость течения жидкости, диаметр трубы и вязкость жидкости, можно расчетным путем определить режим течения жидкости, что очень важно для последующих гидравлических расчетов. Ламинарные течения на практике встречаются в тех случаях, когда по трубам движутся весьма вязкие жидкости, например, смазочные масла, глицериновые смеси и др. Турбулентное течение обычно имеет место в водопроводах, а также в трубах, по которым движутся бензин, керосин, спирты и кислоты. Таким образом, на самолете приходится сталкиваться как с ламинарным, так и с турбулентным режимами течения жидкостей в трубах; в самолетных маслосистемах и гидропередачах режим течения чаще всего ламинарный, а в топливных системах — турбулентный. Смена режимов течения при достижении числа Rекр объясняется тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Re<Reкp ламинарный режим является вполне устойчивым; всякого рода искусственная турбулизация потока и его возмущения (сотрясения трубы, введение в поток колеблющегося тела и пр.) погашаются влиянием вязкости и ламинарный поток восстанавливается. Турбулентный режим при этом неустойчив. При Re>Reкp, наоборот, турбулентный режим устойчив, а ламинарный — неустойчив. В связи с этим критическое число Reкp, соответствующее переходу от ламинарного режима к турбулентному, может получиться несколько больше, чем Reкp для обратного перехода. В особых лабораторных условиях при полном отсутствии факторов, способствующих турбулизации потока, удается получить ламинарный режим при числах Re, значительно больших Reкp. Однако в этих случаях ламинарное течение оказывается настолько неустойчивым, что достаточно, например, небольшого толчка, чтобы ламинарный поток быстро превратился в турбулентный. На практике, особенно в самолетных трубопроводах, мы обычно имеем условия, способствующие турбулизации, — вибрация труб, местные гидравлические сопротивления, неравномерность (пульсации) расхода и пр., а потому указанное обстоятельство имеет в гидравлике скорее принципиальное значение, чем практическое. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается при Re> Re’кp=4000, а при Re=2300—4000 имеет место переходная, критическая область. Вопрос об устойчивости ламинарного режима течения и о механизме турбулизации теоретически пока еще полностью не решен. Но исследования показывают, что в данном сечении цилиндрической трубы турбулизации способствуют такие факторы, как расстояние от стенки, величина скорости и ее поперечного градиента du/dy. Наибольшее расстояние от стенки и наибольшая скорость имеют место в центре потока, но там равен нулю градиент. У стенки, наоборот, градиент скорости наибольший, а скорость и расстояние у наименьшие или даже равны нулю. Поэтому начальная турбулизация ламинарного потока в прямой трубе постоянного сечения начинается где-то в промежутке между осью трубы и стенкой, но все же ближе к стенке. В трубах переменного сечения турбулизация потока происходит не так, как в цилиндрической трубе. В расширяющихся трубах наблюдается замедление течения, усиливается тенденция к поперечному перемешиванию и значение Reкp уменьшается. В сужающихся трубах происходит ускорение течения и выравнивание скоростей по сечению, тенденция к перемешиванию уменьшается, а значение Reкp увеличивается.
ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ Полученное в предыдущем параграфе число Рейнольдса имеет большое значение в гидравлике, а также в аэродинамике, так как является одним из основных критериев гидродинамического подобия. Гидродинамическое подобие — это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое. Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием мы будем понимать подобие тех поверхностей, которые ограничивают потоки жидкостей, т. е. подобие русел (рис. 40). Кинематическое подобие — это подобие линий тока и пропорциональность сходственных скоростей. Очевидно, что для кинематического подобия потоков требуется геометрическое подобие русел.
Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков и равенство углов, характеризующих направление этих сил. В потоках жидкостей обычно действуют разные силы — давления, вязкости (трения), тяжести и др. Соблюдение пропорциональности всех этих разнородных сил означает так называемое полное гидродинамическое подобие. Например, пропорциональность сил давления Р и сил трения Т, действующих на сходственные объемы в потоках / и //, можно написать в виде
Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных сил. Для напорных течений в закрытых руслах, т. е. для потоков в трубах, в гидравлических машинах и т. п., такими главными силами, как показывают расчеты, являются силы давления, трения и их равнодействующие, т. е. силы инерции. Последние, как это можно показать для подобных потоков, пропорциональны произведению динамического давления ru2/2 на характерную площадь S. Для геометрически и кинематически подобных потоков и сходственных частиц можно записать:
Для подобных потоков / и // будем иметь
или
Заметим попутно, что этому же произведению ru2срS в подобных потоках пропорциональны силы, с которыми поток воздействует (или способен воздействовать) на преграды: твердые стенки, лопасти гидромашин, обтекаемые потоком тела и т. п. Так, например, если поток жидкости наталкивается на безграничную стенку (см. рис. 41), установленную нормально к нему, и в результате, растекаясь по стенке, меняет свое направление на 90°, то на основании теоремы механики о количестве движения секундный импульс силы равен
Это и есть сила воздействия на преграду. При другом угле установки стенки или другой ее форме и размерах вместо единицы будет другой коэффициент пропорциональности. Вначале рассмотрим наиболее простой случай — напорное движение идеальной жидкости, т. е. такое движение, при котором отсутствуют силы вязкости, а действие силы тяжести проявляется через давление. Для этого случая уравнение Бернулли для сечений 1—1 и 2—2 (см. рис. 40) имеет следующий вид:
или
Для двух геометрически подобных потоков правая часть уравнения имеет одно и то же значение: следовательно, левая часть тоже одинакова, т. е. разности давлений пропорциональны динамическим явлениям:
Таким образом, при напорном движении идеальной несжимаемой жидкости для обеспечения гидродинамического подобия достаточно одного геометрического подобия. Безразмерная величина, представляющая собой отношение разности давлений к динамическому давлению (или разности пьезометрических высот к скоростной высоте), называется коэффициентом давления или числом Эйлера и обозначается Еu. Посмотрим, какому условию должны удовлетворять те же геометрически и кинематически подобные потоки, для того чтобы было обеспечено их гидродинамическое подобие при наличии сил вязкости, а следовательно, и потерь энергии, т. е. при каком условии числа Ей будут одинаковыми для этих напорных потоков. Уравнение Бернулли теперь будет иметь следующий вид:
или
Как видно из уравнения (5.6), числа Еu будут иметь одинаковые значения для рассматриваемых потоков и потоки будут подобны друг другу гидродинамически при условии равенства коэффициентов сопротивления z, (равенство коэффициентов a1 и a2 для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты z в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков (см. рис. 40) пропорциональны скоростным напорам, т. е.
Рассмотрим очень важный в гидравлике случай движения жидкости — движение с трением в цилиндрической трубе, для которого
Для геометрически подобных потоков отношение l/d одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффициента l. Последний на основании формулы выражается через напряжение трения на стенке tо и динамическое давление следующим образом:
Следовательно, для двух подобных потоков I и II можно записать
т. е. напряжения трения пропорциональны динамическим давлениям. Условие динамического подобия потоков:
или, переходя к обратным величинам,
В этом заключается закон подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамического подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков. Число Re есть величина, пропорциональная отношению динамического давления к напряжению трения или, что то же самое, отношению сил инерции к силам вязкости. Чем больше скорость и поперечные размеры потока и чем меньше вязкость жидкости, тем больше число Re. Для потока идеальной жидкости число Re бесконечно велико, так как вязкость n=0. В случаях безнапорных течений под действием разности нивелирных высот вопрос о подобии осложняется, так как приходится вводить еще один критерий подобия — число Фруда, учитывающее влияние на движение жидкости силы тяжести. Однако для подавляющего большинства интересующих нас задач в области авиационной техники этот критерий не имеет значения, и мы его рассматривать не будем. Итак, в подобных потоках, мы имеем равенство безразмерных коэффициентов и чисел a, z, l, Eu, Ne, Re и некоторых других, которые будут введены и рассмотрены ниже. Изменение числа Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также меняться. Поэтому все эти коэффициенты в общем случае следует рассматривать как функции числа Re (хотя в некоторых интервалах числа Re они могут оставаться постоянными). |




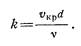







 Последнее отношение, одинаковое для подобных потоков, называется числом Ньютона и обозначается Ne.
Последнее отношение, одинаковое для подобных потоков, называется числом Ньютона и обозначается Ne.