 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Значения параметров химической реакции Б для выполнения задания
Решение. 1.В соответствии со следствием закона Гесса рассчитаем значение
.2. Так как - 2.Рассчитайте DS процесса 2N2(г) + O2(г) = 2N2O(г) Предскажите знак DSо процесса путём анализа уравнения химической реакции Решение. 1.В соответствии со следствием закона Гесса рассчитаем значение
=2*219,9-(2*200+1*205)=-165,2дж/К 2.Согласно стехиометрии уравнения синтеза оксида азота(I) реакция протекает с уменьшением объема системы. Если в реакцию вступало три моля газов, то получено только два моля. Уменьшение объема системы всегда сопровождается уменьшением энтропии системы, что и показывают расчеты: - 3.Определите DGо298 реакции Fe3O4 + 4CO = 3Fe + 4CO2.Установите возможность самопроизвольного протекания процесса в стандартных условиях. РЕШЕНИЕ 1.В соответствии со следствием закона Гесса рассчитаем изменение изобарно-изотермического потенциала
2.Так как значение ------------------------------------------------------------------------------------------------------------------------------------------ 4.Определите стандартный тепловой эффект реакции CH3I +HI=CH4+I2 Решение Согласно справочным данным:
при р=const , в сответствии со следствием закона Гесса, тепловой эффект реакции равен
--------------------------------------------------------------------------------------------------------------------------------------- -- Запишите зависимости теплоемкости каждого вещества в реакции CH3I +HI=CH4+I2 от температуры, учитывая коэффициенты a, b, c, c/. Решение Согласно справочным данным:
выразим зависимости теплоемкости каждого вещества от температуры, учитывая коэффициенты: Cp(CH3I)=19,67+92,67*10-3T-32,28*10-6 T2 Cp(CH4)= 14,32+74,66*10-3T -17,43*10-6 T2 Cp(HI)= 26,32+5,94*10-3T +0,92*105 T-2 Cp(I2)= 37,40+0,59*10-3T -0,71*105 T-2 6. Рассчитайте суммы теплоемкостей исходных веществ и суммы теплоемкостей продуктов реакции CH3I +HI=CH4+I2, на основании которых сделайте вывод об увеличении или уменьшении теплового эффекта химической реакции с увеличением температуры. По полученным данным постройте графики зависимостей суммы теплоемкостей исходных веществ и продуктов реакции CH3I +HI=CH4+I2 от температуры Решение 1. Расчет суммы теплоемкостей исходных веществ ведем по формуле: ∑Ср(исходных веществ)= Cp(CH3I)+ Cp(HI) = (19,67+26,32) +(92,67+5,94) *10-3T -32,28*10-6 *T2+0,92*105 T-2=45,99 +98,61*10-3T -32,28*10-6 T2+0,92*105 T-2 2. Расчет суммы теплоемкостей продуктов реакции ведем по формуле: ∑Ср(продуктов )= Cp(CH4)+ Cp(I2)=(14,32+37,40)+(74,66+0,59) *10-3T -17,43*10-6 T2-0,71*10-5 T-2 =51,72+75,25*10-3T -17,43*10-6 T2-0,71*105 T-2 3. Для сравнения ∑Ср(исходных веществ) и ∑Ср(продуктов ) рассчитываем соответствующие значения при температурах, равных 298 К, 400 К, 600 К, 1000 К. Результаты расчетов приведены в таблице1 и на графике 1: Таблица 1 Теплоемкости продуктов и исходных веществ
Рис. 1. Зависимость теплоемкостей продуктов реакции и исходных веществ от температуры Поскольку теплоемкость исходных веществ больше, чем теплоемкость продуктов, тепловой эффект реакции с увеличением температуры будет уменьшаться. - 7.Рассчитайте тепловой эффект реакции при температурах, равных 298 К, 400 К, 600 К, 1000 К. По полученным данным постройте графики зависимостей суммы теплоемкостей исходных веществ и продуктов реакции CH3I +HI=CH4+I2 от температуры, а также теплового эффекта химической реакции от температуры. Решение Рассчитаем тепловой эффект реакции при температурах 298 К, 400 К, 600 К, 1000 К. 1.Согласно справочным данным:
при р=const , в сответствии со следствием закона Гесса, стандартный тепловой эффект реакции равен
2.Рассчитываем изменение эмпирических коэффициентов: Δа=а(СН4)+а(I2)-а(CH3I)-а(HI)=5,73 Δb= b(СН4)+b(I2)-b(CH3I)-b(HI)=-23,36*10-3 Δc= с(СН4-с(CH3I) =14,85*10-6 Δc⁄= c⁄ (I2)- c⁄ (HI)=-1,63*105 3.Рассчитываем тепловой эффект реакции при 400 К, 600 К, 1000 К по уравнению
где ΔН1 ΔН=-59680+5,73(Тi-298)-0,5*23,36*10-3 (Тi2-2982)+(14,85/3) *10-6 * (Тi3-2983)-1,63*105 (298-1- Тi-1) Значение тепловых эффектов пр и разных температурах, полученные в ходе расчетов, приведены в таблице1, зависимость теплового эффекта от температуры показана на рис 1 Таблица 1. Значения тепловых эффектов пр и разных температурах
Рис. 1.Зависимость теплового эффекта от температуры - - 8.Для вещества СН3I химической реакции CH3I +HI=CH4+I2 напишите уравнение, выражающее зависимость изменения энтропии в изобарном процессе его нагревания от 0 К до 1000 К с учетом всех возможных изменений агрегатного состояния. Решение Для вычисления изменения энтропии в реальном необратимом процессе нагревания CH3I от 0 К до 1000 К, этот процесс (мысленно) разобьем на 5 обратимых стадий: нагревание CH3I(тверд) до температуры плавления, плавление CH3I, нагревание жидкого CH3I до температуры кипения, испарение, нагревания газа CH3I. Определим изменение энтропии (ΔS) на каждой из этих стадий: 1.1Нагревание CH3I (тверд) от Т1(0 К)до 206,55 К (tплавл CH3I = -66,45°Сили 206,55 К). Изменение энтропии на этой стадии обозначим как ΔS1: ΔS1 =Cpln 1.2.Стадия фазового перехода – плавление CH3I (ΔS2): ΔS2 =
1.3. Стадия нагревания жидкого CH3I от Т1=206,55К до Т2=315,43 К (tкипения CH3I =42,43°С или 315,43 К ). Изменение энтропии на этой стадии (ΔS3), рассчитывается по формуле: ΔS3=аln где а, b, с – коэффициенты зависимости теплоемкости от температуры. Подставляя соответствующие значения, получаем: ΔS3=19,67ln 1.4.Стадия фазового перехода – испарение CH3I (ΔS4): ΔS4 1.5. Стадия нагревания газа CH3I от Т=315,43 К до 1000 К: ΔS5=аln где а, b, с – коэффициенты зависимости теплоемкости от температуры, V2 и V1 – объемы газов при Т2 и Т1. При изобарном процессе ΔS5=19,67ln +8,31ln 1.6Уравнение, выражающее зависимость изменения энтропии в изобарном процессе нагревания CH3I от 0 К до 1000 К с учетом всех возможных изменений агрегатного состояния, основано на суммировании изменений энтропии всех обратимых стадий. При этом получают изменение энтропии в данном необратимом процессе., Т.о. ΔS∑ =∑ ΔSi
ΔS∑= Cpln ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 9.Выразите уравнением зависимость энтропии вещества СН3I от температуры в интервале температур от 298 до 1000 К. При выводе уравнения учесть только коэффициенты a, b зависимости теплоемкости вещества от температуры. Решение Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:
Интегрирование этого выражения от 298 К до T , с учетом коэффициентов a и b зависимости теплоемкости СН3I от температуры приводит к выражению:
Согласно справочным данным, коэффициенты зависимости теплоемкости вещества от температуры:
Тогда уравнение зависимости энтропии СН3I от температуры в интервале температур от 298 до 1000 К принимает вид: S(Т)=253+ 19,67ln 10.Определите изменение энтропии в ходе реакции CH3I +HI=CH4+I2, протекающей в идеальном газообразном состоянии при температуре Т, равной 298 К. Решение На основании справочных значений энтропий веществ, участвующих в реакции:
Рассчитаем изменение энтропии реакции :
_____________________________________________________________________________________ 11.Для одного моля вещества СН3I химической реакции CH3I +HI=CH4+I2, находящегося в идеальном газообразном состоянии при температуре Т, равной 600 К, определите изменение энергии Гиббса и энергии Гельмгольца при изменении давления на 1000 Па. Решение 1. Изменения энергии Гиббса(ΔG) и энергии Гельмгольца (ΔF)в изотермическом процессе расширения или сжатия 1 моля идеального газа рассчитываются по формуле: ΔG = ΔF= RTln где Р2 и Р1- соответственно, конечное и начальное давление. Увеличение давления сопровождается увеличением энергии Гиббса и энергии Гельмгольца и наоборот. Найдем ΔG и ΔF при повышении давления на 1000 Па от Р1 =105Па (1 атм)до Р2=1,01*105Па: ΔG =ΔF =8,31*600*ln 12.Определите изменение энергии Гиббса и энергии Гельмгольца при нагревании СН3I от 298 до 600 К. Решение Зависимость энергии Гиббса и энергии Гельмгольца от температуры можно описать с помощью основного уравнения термодинамики:
ΔG и ΔF при нагревании 1 моля CH3I от 298 до 600 К можно найти, проинтегрировав частную производную по температуре:
13.На основании справочных значений определите изменение энергии Гиббса и энергии Гельмгольца в ходе реакции CH3I +HI=CH4+I2, протекающей в идеальном газообразном состоянии при температуре Т, равной 298 К. Решение Согласно справочным данным найдем изменение энергии Гиббса и энергии Гельмгольца в ходе заданной химической реакции, протекающей в идеальном газообразном состоянии при температуре Т, равной 298 К:
1. В соответствии со следствием закона Гесса, тепловой эффект реакции равен
2. Рассчитаем изменение энтропии реакции :
3.Найдем ΔGr в соответствии с выражением: ΔGr=ΔHr-TΔSr=-59,68-298*0,01253=-64,4 кдж 4.Изменение энергии Гельмгольца в реакции между идеальными газами связано с энергией Гиббса уравнением: ΔGr = ΔFr+ΔnRT, где Δn - изменение количества молей газообразных веществ в ходе реакции. В рассматриваемой реакции CH3I (г)+HI (г)=CH4(г)+I2(г) Δn =0, Т.о. ΔGr = ΔFr=-64,4 кдж 14.Для реакции CH3I (г)+HI (г)=CH4(г)+I2(г),протекающей в идеальном газообразном состоянии, выразите в общем виде константы равновесия Кp, Кc, Кx, Кn через равновесное количество молей вещества СН4, равное х, если исходные вещества CH3I и HI взяты в стехиометрических количествах при давлении Р и при температуре Т. Решение 1. Константа химического равновесия может быть выражена через парциальные давления (Pi), молярные концентрации (Сi) и мольные доли компонентов (хi, ni). В общем виде для рассматриваемой реакции выражения для констант будут выглядеть следующим образом:
Между Кp, Кc, Кx, Кn существуют взаимосвязи, выражаемые уравнениями:
где Т.о. , для рассматриваемой реакции Кp= Кc= Кx= Кn. Для того, чтобы найти численное значение Кp (Кc, Кx, Кn), рассчитаем равновесные парциальные давления компонентов, используя значения, представленные в таблице5.1. Таблица 5.1.
РCH3I= Выразим константу равновесия Кр:
Выразим константу равновесия Кх(Кn):
Выразим константу равновесия Кс:
_____________________________________________________________________________________ 15.Обоснуйте влияние увеличения общего давления на равновесный выход продуктов реакции CH3I (г)+HI (г)=CH4(г)+I2(г). Как скажется на равновесном выходе продуктов реакции разбавление реакционной смеси газом, не участвующим в химической реакции. Проанализируйте, как влияет увеличение температуры на выход продуктов реакции. Решение 1. Поскольку в ходе химической реакции число моль компонентов не меняется (Δn = 0), то изменение давления не влияет на положение равновесия химической реакции, т.е. не скажется на равновесном выходе. 2. Поскольку разбавление реакционной смеси газом, не участвующим в химической реакции, приведет к одинаковому уменьшению концентраций всех реагентов, оно не скажется на равновесном выходе продуктов реакции. 3. Поскольку прямая реакция является экзотермической ( 16.Какая термодинамическая функция является критерием самопроизвольно протекающих процессов при постоянном давлении и температуре? Каково значение этой функции для реакции CH3I (г)+HI (г)=CH4(г)+I2(г)при 298 и 600 К? Сделайте вывод о направлении самопроизвольного процесса при 600 К, если парциальные давления всех компонентов в реакции CH3I (г)+HI (г)=CH4(г)+I2(г)равны по 0,5 атм. Решение 1.Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным TΔS, обусловленным увеличением беспорядка в системе вследствие роста её энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж): G = H – TS или ∆G= ∆H– ∆(TS). Изменение свободной энергии Гиббса является критерием самопроизвольно протекающих процессов при постоянном давлении и температуре. По изменению энергии Гиббса можно определить : ∆G <0 — процесс необратимый, самопроизвольный; ∆G= 0 — состояние равновесия в системе; ∆G >0 — процесс необратимый, несамопроизвольный. 2.Найдем значения ∆G при 298 и 600 К: 2.1.Согласно справочным данным найдем изменение энергии Гиббса и энергии Гельмгольца в ходе заданной химической реакции, протекающей в идеальном газообразном состоянии при температуре Т, равной 298 К:
1 В соответствии со следствием закона Гесса, тепловой эффект реакции равен
Рассчитаем изменение энтропии реакции :
Найдем ΔGr в соответствии с выражением: ΔGr=ΔHr-TΔSr=-59,68-298*0,01253=-64,4 кдж 2.∆G600 = ∆Н600– 600*∆S600; Рассчитаем тепловой эффект реакции при 600 К по уравнению
где ΔН1 Эмпирические коэффициенты зависимости теплоемкости от температуры представлены в таблице:
Рассчитываем изменение эмпирических коэффициентов: Δа=а(СН4)+а(I2)-а(CH3I)-а(HI)=5,73 Δb= b(СН4)+b(I2)-b(CH3I)-b(HI)=-23,36*10-3 Δc= с(СН4-с(CH3I) =14,85*10-6 Δc⁄= c⁄ (I2)- c⁄ (HI)=-1,63*105 ΔН=-59680+5,73(Тi-298)-0,5*23,36*10-3 (Тi2-2982)+(14,85/3) *10-6 * (Тi3-2983)-1,63*105 (298-1- Тi-1)=-60454 дж Для нахождения ∆S600 воспользуемся уравнением:
Рассчитаем изменение стандартной энтропии реакции :
Тогда ∆S600 =12,53+5,73*ln(600/298)- 23,36*10-3(600-298) +0,5*14,85*10-6(6002-2982)+0,5*1,63*105(1/6002-1/2982)=10,8 дж ∆G600 = ∆Н600– 600*∆S600=-60454 -600*10,8=-66934 дж=-66,9 кдж 2. 2. Связь между концентрациями реагентов и общими условиями термодинамического равновесия устанавливает уравнение изотермы химической реакции:
где ΔG – изменение энергии Гиббса в ходе химической реакции, Кр– константа равновесия химической реакции,
3. Если парциальные давления всех компонентов (P/i) равны по 0,5 атм, выражение для
Тогда ∆G600=RTln1- RTlnKp=0- RTlnKp. Из этого выражения найдем Kp= exp(-∆G/ RT) = exp(66934/ (8,31*600)) =6,8*105. Т.К. Kp>1, равновесие сдвинуто в сторону образования продуктов реакции, самопроизвольный процесс направлен вправо. _____________________________________________________________________________________ 17.Приведите уравнение изобары реакции CH3I (г)+HI (г)=CH4(г)+I2(г) и рассчитайте константы равновесия Кp при 298 К, 400 К и 600 К. На основании этих данных вычислите средний тепловой эффект химической реакции в интервале от 298 К до 600 К. Постройте график зависимости логарифма константы равновесия от температуры и по нему определите константы равновесия при 700 К. Решение 1.Уравнение изобары в дифференциальном виде:
Для того, чтобы вычислить насколько изменится константа равновесия в результате изменения температуры на определенную величину, уравнение изобары следует проинтегрировать. Примем, что тепловой эффект химической реакции в небольшом интервале температур постоянен и не зависит от температуры (ΔH=const). Проведем интегрирование уравнения изобары химической реакции:
Получим уравнение:
Рассчитаем значения Кр при Т= 298 К, 400 К и 600 К. В расчетах используем результаты, полученные в ходе выполнения заданий 1 и 2:
Δа=а(СН4)+а(I2)-а(CH3I)-а(HI)=5,73 Δb= b(СН4)+b(I2)-b(CH3I)-b(HI)=-23,36*10-3 Δc= с(СН4-с(CH3I) =14,85*10-6 Δc⁄= c⁄ (I2)- c⁄ (HI)=-1,63*105 Кр=EXP(-59680/RT+5,73/R*lnT-(23,36*10-3/2R)*T+(14,85*10-6/6R)*T2-(1,63*105/2R)*T-2) В результате расчетов получены следующие значение Кр (таблица 7.1): Таблица 7.1. Значения констант равновесия
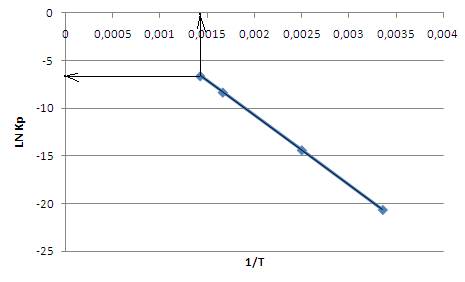
2.Для вычисления среднего теплового эффекта химической реакции в интервале от 298 К до 600 К построим график зависимости lnKp=f(1/T) (рис7.1). Ее аналитическое выражение, как вытекает из интегральной формы изобары химической реакции, выглядит следующим образом:
Рис.7.1. График зависимости lnKp=f(1/T)
Тангенс угла наклона графика (-7313) равен отношению теплового эффекта химической реакции к универсальной газовой постоянной. Рассчитаем средний тепловой эффект реакции в интервале от 298 К до 600 К по формуле: ΔН=R*tgα=8,32*(-7313)=-60771 дж. Сопоставляя это значение со значениями, вычисленными в задании 2, видим их сходство: Таблица 7.2.
3. По графику (рис.7.2) определим константу равновесия при 700 К: lnK=-6,6, Kp=0,0014
Рис.7.2. Графическое определениеконстанты равновесия 18.Что называется фазой, компонентом, числом независимых компонентов, числом термодинамических степеней свободы? Приведите их количество для реакции CH3I (г)+HI (г)=CH4(г)+I2(г). Решение 1.Фазойназывается часть гетерогенной системы, ограниченная поверхностью раздела и характеризующаяся одинаковыми во всех точках физическими и химическими свойствами. 2. Если между составляющими веществами нет химического взаимодействия, то состав каждой фазы системы при любых условиях однозначно выражается через концентрации составляющих веществ и, в этом случае они называются компонентами. Число независимых компонентов равняется наименьшему числу составляющих веществ системы, достаточных для определения состава любой фазы системы. Его определяют по следующей формуле: К= s – n – m, где s – число составляющих веществ системы, n – число независимых обратимых химических реакций, m – число соотношений между концентрациями веществ. 3. Число термодинамических степеней свободы– число независимых координат, полностью определяющих положение системы в пространстве.Оноопределяется в соответствии с правилом фаз Гиббса формулируется следующим образом:, или вариантность равновесной термодинамической системы С, определяется как разность числа независимых компонентов системы К и числа сосуществующих фаз Ф плюс число внешних факторов n, влияющих на равновесие.Его математическое выражение записывается в виде соотношения: С = К – Ф + n.При переменных давлении и температуре правило фаз сводится к выражению:С = К – Ф +2 4. Определим количество независимых компонентов и число термодинамических степеней свободы для заданной реакции CH3I(г) +HI(г)=CH4(г)+I2(г)
4.1. Число независимых компонентов = К= s – n – m, Где s – число составляющих веществ системы =4 n – число независимых обратимых химических реакций, =1 m =1, т.к. мольные доли и, соответственно, парциальные давления продуктов будут связаны соотношением: т.о. число независимых компонентов =4-1-1=2. Зная концентрации исходных веществ , можно определить концентрации каждого из продуктов. 4.2. Число термодинамических степеней свободы С= К– Ф+ 2 К=2, Ф=1, т.к. все вещества – газы, т.о. С= К– Ф+ 2 =2-1+2=3 степени свободы 19.На основании зависимости общего давления в реакционной смеси от времени протекания реакции 2F2O = 2F2+O2при постоянном объеме V=1m3 и температуре 523 К
определить парциальное давление исходного вещества Рисх в Н/м2 в моменты времени τ построить график зависимости парциального давления исходного вещества Рисх от времени, lg P исх=f(τ ) и Решение 1.Определение парциального давления исходного вещества Рисх в моменты времени τ 1.1. Найдем первоначальное количество исходного вещества F2O и суммарные количества веществ в реакционной смеси в моменты времени τ по формулам: n0(F2O)=P0*V0/RT n τ (реагентов)=P τ *V0/RT 1.2. Пусть к моменту времени τ прореагирует аτ моль F2O. Рассчитаем равновесные парциальные давления компонентов, используя значения количеств реагентов, представленные в таблице 1: Таблица 1. Баланс количеств веществ реагентов
Находим аτ из выражения n τ=1+0,5 аτ, т.е. аτ =2*( n τ-1) n τ (F2O) =1- аτ =1- 2*( n τ-1)=3-2 n τ Найдем мольную долю исходного вещества в момент времени τ (х τ (F2O)) и его парциальное давление Р τ (F2O); х τ (F2O)= n τ (F2O)/ n τ =(1- 2*( n τ-1))/ n τ Р τ (F2O) = х τ (F2O)* Р τ Результаты расчетов (n τ, n τ (F2O), а τ (F2O), Р τ (F2O) внесены в таблицу2:
Таблица 2. Данные расчетов парциальных давлений
2. График зависимости парциального давления исходного вещества Рисх (Р τ (F2O) )от времени представлен на рис. 1
Рис. 1. График зависимости парциального давления исходного вещества Рисх (Р τ (F2O) )от времени 3. Кинетические уравнения первого, второго и третьего порядков в дифференциальном и интегральном виде:
4. Вычислим lg P исх и Таблица 3. Значения lg P исх и
5. Построим графики зависимости lg P исх=f(τ ) и
Рис. 2 График зависимости lg P исх=f(τ )
Рис. 3 График зависимости 6. Оба графика представляют собой прямые линии. Принимаем, что у реакции – первый порядок. 7. Определим константу скорости реакции: k =-2,3tg α, где α – угол наклона графика к оси абсцисс. К находили с помощью метода наименьших квадратов. Полученные значения k, выраженные в разных размерностях, представлены ниже: k=3,73*10-6с-1= 0,00023мин-1=0,0134 час-1 8. Запишем кинетическое уравнение для реакции в дифференциальном и интегральном виде, используя значение k в размерности с-1: 8.1. дифференциальный вид: dР/dτ = k*(Р0(F2O)- Р τ (F2O)) =3,73*10-6*(4348- Р τ (F2O)) 8.2. интегральный вид : Р τ (F2O)= Р0(F2O)*
9.С помощью кинетического уравнения определим количество молей исходного вещества, которое прореагировало к моменту времени τ1=104с 9.1 С помощью интегральной формы кинетического уравнения найдем парциальное давление Р τ (F2O) в данный момент: Р τ (F2O)=4188 н/м2 9.2. найдем количество вещества, содержащееся в реакционной смеси к моменту τ1: n τ (F2O)= Р τ (F2O)*1/(8,31*523)=0, 96моль 9.3. найдем прореагировавшее количество вещества n прореаг (F2O)= n 0 (F2O)- n τ (F2O)= 1-0,96=0,04моль 10. Определим общее давление в системе в момент времени τ1: 10.1. Общее количество молей реагентов в системе( n τ ) равно (из п. 1.2.): n τ=1+0,5а, где а = n прореаг (F2O), т.е. n τ=1+0,5*0,04=1,02моль 10.2 Мольная доля F2O в момент времени τ1 равна: х τ (F2O)= n τ (F2O)/ n τ= 0,96/1,02=0,9412 10.3. Общее давление Рτ = Р τ (F2O)/ х τ (F2O)=4435 н/м2 11. Определим время, за которое прореагирует 10 % исходного вещества: 11.1. Найдем сумму моль всех компонентов в смеси и мольную долю F2O к этому моменту: n τ = 1+0,5*0,1=1,05моль х τ (F2O)= n τ (F2O)/ n τ=0,9/1,05=0,857
11.2. Найдем Робщ в системе : Робщ= n τ*R*T/V=1,05*8,31*523/1=4563н/м2 11.3 Найдем Р (F2O) = х (F2O)* Р общ=0,857*4563=3910 н/м2 11.4 На основании кинетического уравнения найдем τ (10%)=41450 сек. 12. Определим период полупревращения для рассматриваемой реакции :
20.Определите концентрации веществ А, В и С в периоды времени от 1 до 10 ч через каждый час, если в реакционном сосуде протекает при некоторой температуре реакция первого порядка:
Исходная концентрация вещества А 1 моль/л.Определите время достижения максимальной концентрации вещества В, τmax Как изменится τmax, если k2 увеличится, а k1 останется без изменения? Определите максимальную концентрацию вещества В в моль/л. На основании данных, полученных выше, постройте график зависимости концентрации веществ А, В и С от времени. Графически определите концентрации веществ А, В и С при времени 4,5 ч. Определите время, за которое прореагирует половина вещества А. Значения констант скоростей химических реакций: k1, =0,5ч-1, k2, =0,3 ч-1 Решение 1. Определим концентрации веществ А, В и С в периоды времени от 1 до 10 ч через каждый час по следующим формулам:
Результаты приведены в таблице1: Таблица 1. Расчетные данные
2.Определим время достижения максимальной концентрации вещества В, τmax с помощью формул:
Тогда γ =0,3/0,5=0,6. τmax= 3. Если k2 увеличится, а k1 останется без изменения, время достижения максимальной концентрации вещества В, τmax, уменьшится. 4. Максимальную концентрацию вещества В определим по формуле:
Свmax=1*0,61,5=0,465 моль/л 5. На основании данных, полученных выше, построим график зависимости концентрации веществ А, В и С от времени, графически определим концентрации веществ А, В и С при времени 4,5 ч, . Рис. 1. Зависимости концентрации веществ А, В и С от времени СА(4,5 час)=0,1 моль/л, СВ(4,5 час)=0,385 моль/л, Сс(4,5 час)=0,5 моль/л 6. Определим время, за которое прореагирует половина вещества А, по формуле для реакции первого порядка: τ1/2=ln2/k1=1,39 час 21. На основании константы скорости реакции 2F2O=2F2+O2
вычертите график зависимости lgk=f( Решение 1. В таблице 1приведены значения констант скорости реакции 2F2O=2F2+O2 при разных температурах: Таблица 1. Значения констант скорости реакции 2F2O=2F2+O2
Ниже приведен график зависимости lnk=f(
Рис. 1. Зависимость lnk=f(
2. Определим графически энергию активации реакции А в кДж/моль: tgα = тогда 3. Определим аналитически энергию активации реакции А в кДж/моль: Еа= 3.1. Т1=523К, k1=0,0134 ; Т2=543 К,k2=0,0572; Еа1= 171057 дж/моль 3.2. Т1=523К, k1=0,047; Т3=583 К, k3=0,6908; Еа2=166309 дж/моль 3.3.Т2=543 К, k2=0,0572; Т3=583 К, k3=0,6908; Еа3=163661 дж/моль 3.4.Среднее значение Еа=167 кдж/моль Сравним значения, определенные графически и аналитически: Еа (граф.)=
4. Определим предэкспоненциальный множитель в уравнении Аррениуса: Отрезок, отсекаемый на оси ординат равен lnА=33,94, A=5,5*1014c-1 5. Запишем уравнение Аррениуса для реакции А: k=5,5*1014e-167000/(RT) 6. С помощью уравнения Аррениуса определим константу скорости реакции А при температуре Т3=500К k3 =5,5*1014e-167000/(8,314*500)=0,00196 с-1 7. Определим температурный коэффициент скорости γ реакции А в интервале температур от Т1 ( 543 К) до Т2(583К)
Отсюда γ=1,864 8. На основании температурного коэффициента скорости реакции определим во сколько раз изменится скорость, если температура повысится на 25 °С:
Т.о. при повышении температуры на 25 °С скорость реакции повысится в 4,745 раз.
22.Вычислите энтропию активации на основании экспериментального значения энергии активации и константы скорости реакции Б при температуре Т, К.На основании некоторой предполагаемой структуры активированного комплекса реакции Б, обладающего тремя степенями свободы колебательного движения с характеристическими температурами θ1 , θ2, θ3 , определите колебательную составляющую энтропии активированного комплекса при температуре Т, К. Определите поступательную составляющую энтропии активированного комплекса при температуре Т, К. При расчете воспользуйтесь уравнением:
Определите вращательную составляющую энтропии активированного комплекса при температуре Т, К, зная его момент инерции J и степень симметрии σ. При расчете воспользоваться уравнением: . Определите абсолютную энтропию активированного комплекса. Сделайте заключение о справедливости предполагаемой модели активированного комплекса.. Значения параметров химической реакции Б для выполнения задания
Решение Решение 1.К основным положениям теории абсолютных скоростей реакции (иначе - теории активированного комплекса, терии переходного состояния, 1935, Эйринг , Поляни и Эванс) могут быть отнесены следующие: · частицы реагентов при взаимодействии теряют свою кинетическую энергию, которая превращается в потенциальную, и для того чтобы реакция свершилась, необходимо преодолеть некий барьер потенциальной энергии; · разница между потенциальной энергией частиц и упомянутым энергетическим барьером - энергия активации; · переходное состояние находится в равновесии с реагентами; · в тех реакциях, где энергия активации существенно ниже энергии разрыва химических связей, процессы образования новых связей и разрушения старых связей могут полностью или частично совпадать по времени. 2. Исходным общим выражением для кинетических уравнений реакций в теории абсолютных скоростей является следующее:
где С≠- число частиц реагентов в единице объема, находящихся в переходном состоянии (ПС), τ≠ - характеристическое время жизни частиц в ПС. Это время прохождения через вершину потенциального барьера. Константа скорости k находится в соответствии с уравнением:
где kB = 1,38*10-23 Дж/К - постоянная Больцмана, h = 6,63*10-34 Дж. с - постоянная Планка, 2.3. В статистическом подходе константу равновесия выражают через суммы по состояниям, тогда кинетическое уравнение принимает вид::
где 2.4.В термодинамическом подходе константу равновесия выражают через разность термодинамических функций активированного комплекса и исходных веществ. Для этого константу равновесия, выраженную через концентрации, переводят в константу, выраженную через давления. Для мономолекулярной реакции, в которой образование активированного комплекса происходит без изменения числа частиц, константа скорости выражается следующим образом:
Для бимолекулярной реакции, протекающей в газовой фазе, в эту формулу добавляется множитель RT / P0 (где P0 = 1 атм = 101.3 кПа), который нужен для перехода от
3. Изобразим схематично зависимость потенциальной энергии системы от пути реакции при протекании реакции типа (рис.13.1.): XY+ Z=X+ YZ |
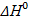(реакции):
=(2*0+2*33)-2*(-124)=314 кДж
(реакции):
=
(реакции)=( 
=(3*0+4*(-394))-(1*(-1014)+4*(-137,2))=-13,2 кДж
, кДж/моль
=(-74,85+62,24)-(20,5+26,57)=-59,68 кдж. Ответ: 
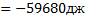, Т1 
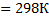, Т2 
.
+b(T2-T1) +0,5c( 
),
+0,09267 (315,43-206,55) -0,5*32,28*10-6(315,432-206,552)=17,5 дж
, тогда:
+0,09267 (1000-315,43) +0,5*32,28*10-3 (10002 -315,432)
+ 
+ 
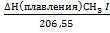98,69
.
+0,0967*(T-298)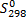
, Дж/моль*K
=12,53 дж/К
,
=49,6дж
=-5200 дж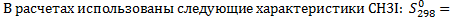
253 Дж/моль*K, Cp =44,1дж/моль*К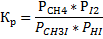
,
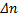- изменение стехиометрических коэффициентов реагирующих газообразных веществ: Δn=(1+1)-(1+1)=0
*Р, РHI= 
*Р, РI2= 
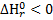), с увеличением температуры равновесие сдвигается в сторону образования исходных веществ, выход продуктов реакции уменьшается.
.
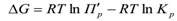
– произведение начальных (неравновесных) парциальных давлений:
= 
= 
=1
,
=f(τ ), определить порядок реакции. Определите константу скорости реакции .Записать кинетическое уравнение для реакции в дифференциальном и интегральном виде. Определить количество молей исходного вещества, которое прореагировало к моменту времени τ1, определить общее давление в системе в момент времени τ1, определить время, за которое прореагирует 10 % исходного вещества, определить период полупревращения для рассматриваемой реакции.
для всех значений времени. Результаты – в таблице 3:
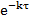=4348* 
с
). Определите графически энергию активации реакции А в кДж/моль. Определите аналитически энергию активации реакции А в кДж/моль. Определите предэкспоненциальный множитель в уравнении Аррениуса. Запишите уравнение Аррениуса для реакции А. Определите константу скорости реакции А при температуре Т3. Определите температурный коэффициент скорости γ реакции А в интервале температур от Т1 до Т2. На основании температурного коэффициента скорости реакции определите во сколько раз изменится скорость, если температура повысится на 25 °С?
) (рис. 1)
, где α – угол наклона графика к оси абсцисс
Еа (аналит.)=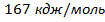 
. Различие между значениями не превышает 1%.
=4,745 раз.
,
- константа равновесия образования активированного комплекса, выраженная через молярные концентрации (в моль/л). В зависимости от того, как оценивают константу равновесия, различают статистический и термодинамический аспекты ТАК.
- полная сумма по состояниям активированного комплекса, Q реаг - произведение полных сумм по состояниям реагентов, 
- энергия активации при абсолютном нуле
.
.