 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приклади розв’язування задач.
Задача №1.Під час маневрування на станції паровоз надав вагонові масою 40000 кг швидкості 5 м/сек. Вагон, пройшовши певний шлях, ударився буферами об буфери загальмованого вагона. Пружини кожного буфера стиснулися на 10 см. Який шлях пройшов вагон від моменту надання йому швидкості до зіткнення з нерухомим вагоном, якщо відомо ,що пружини стискаються на 1 см на кожні 49000 н, а коефіцієнт опору при русі вагона по рейках становить 0,01? Розв’язування. Виходимо з закону збереження і перетворення енергії, за яким набута вагоном кінетична енергія витрачається на виконання роботи проти сил опору на шляху s, а також на стискання буферних пружин. Отже, можемо записати
Робота стискання однієї пружини
де -
Підставивши числові дані, одержимо s=100 м. Задача № 2. Камінь кидають під кутом 30° до горизонту. Кінетична енергія каменя в початковий момент становить 60 дж Нехтуючи опором повітря, треба знайти кінетичну і потенціальну енергії каменя у найвищій точці траєкторії. Розв’язування. Для визначення потенціальної енергії каменя у найвищій точці траєкторії знайдемо максимальну висоту підйому каменя
Тоді
Враховуючи, що За законом збереження і перетворення енергії
Розв’язування. Під дією тягаря Р (рис. 1) обидві пружини розтягнуться відповідно на
Величину розтягу можна визначити так:
Задача №.4 Невеликий за розмірами тягар масою m2 прикріплений до вірьовки довжиною l і масою m, яка лежить на гладенькому горизонтальному столі. Під дією ваги тягаря вірьовка починає сповзати через отвір у столі без початкової швидкості. Якою буде швидкість вірьовки в момент, коли її кінець сповзе з стола? Розв’язування. Коли кінець вірьовки сповзе зі стола, кінетична енергія центра ваги системи дорівнюватиме зміні потенціальної енергії системи. Обчислимо різницю потенціальних енергій для двох положень вірьовки з тягарем: вірьовка повністю лежить на столі і вірьовка повністю сповзла з стола. Спочатку визначимо положення центра ваги системи. Позначивши через х відстань центра ваги від тягаря m1 , можемо записати
Коли вірьовка повністю сповзе з стола, центр ваги системи буде знаходитися на відстані
від поверхні стола і зміна потенціальної енергії буде дорівнювати На основі закону збереження енергії маємо Задача №5. Кран піднімає вантаж масою 2т на висоту 24 м за 2хв. Знайти потужність крана. Силою тертя знехтувати. Розв¢язування:Потужність рівна відношеню механічної роботи до часу, який затрачено на виконання цієї роботи.
Механічна робота зовнішніх сил при підняті вантажу буде рівна зміні його потенційної енергії,
За нулбовий рівень приймемо точку коли вантаж знаходиться на землі. В цій точці початкова висота буде рівна нулю. Тоді
Підставивши значення механічної роботи в формулу потужності маємо:
Перевівши всі величини в систему СІ та підставивши в кінцеву формулу маємо:
Задача №6. Літак має чотири двигуна, сила тяги кожного становить 103кН. Яка корисна потужність двигунів при польоті літака зі швидкістю 864м/с? Розв¢язування:Корисна потужність двигунів рівна відношеню механічної роботи до часу.
Механічна робота яку здійснює літак при польоті рівна добутку сили на переміщення яке здійснив літак.
Підставивши значення механічної роботи в формулу потужності маємо:
З формули видно, що відношення переміщення на час є швидкість літака.
Підставивши вираз (4) в (3) маємо
Підставивши дані в формулу (5) знайдемо потужність літака
|





 — середнє значення сили стискання. Звідси
— середнє значення сили стискання. Звідси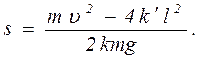


 , дістанемо Еп=15Дж.
, дістанемо Еп=15Дж.
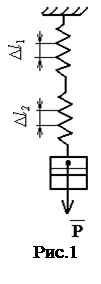 Задача № 3. До нижнього кінця пружини, підвішеної вертикально, приєднана друга пружина, до кінця якої прикріплений тягар. Коефіцієнти пружності пружин становлять відповідно k1 i k2. Нехтуючи вагою пружин порівняно з вагою тягаря, знайти відношення потенціальних енергій цих пружин.
Задача № 3. До нижнього кінця пружини, підвішеної вертикально, приєднана друга пружина, до кінця якої прикріплений тягар. Коефіцієнти пружності пружин становлять відповідно k1 i k2. Нехтуючи вагою пружин порівняно з вагою тягаря, знайти відношення потенціальних енергій цих пружин. і
і  . Виконана тягарем робота по розтягуванню пружин за рахунок своєї потенціальної енергії йде на збільшення потенціальної енергії пружин. Робота, виконана тягарем по розтягуванню першої пружини,
. Виконана тягарем робота по розтягуванню пружин за рахунок своєї потенціальної енергії йде на збільшення потенціальної енергії пружин. Робота, виконана тягарем по розтягуванню першої пружини,

 і
і  , тоді
, тоді 
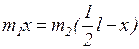 , звідки
, звідки 

 , звідки
, звідки 
 ,
,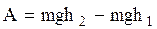 ,
,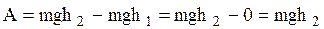 ,
, ,
, .
. , (2)
, (2) , (3)
, (3) , (4)
, (4) , (5)
, (5)