 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приклади розв’язування задач.
Задача№1. Дві гирі масою 5 і 3 кгпідвішені на кінцях нитки, перекинутої через блок, причому менша гиря знаходиться на 1 м нижче від більшої. Якщо надати гирям можливості рухатися під дією сил тяжіння, то через який час гирі будуть на однаковій висоті? Розв’язування. Система буде рухатися з одним і тим же прискоренням а в бік більшої гирі. На кожну гирю діють сила тяжіння і сила натягу ниткице показано на рис.11. Сили і прискорення, направлені вниз, умовимося вважати додатними, вгору — від'ємними. Тоді записати другим законом динаміки для кожного з тіл окремо: m1a=m1g-F1 –m2a=m2g-F2 Оскільки нитка і блок невагомі, то F1=F2. Віднявши від першого рівняння друге, дістанемо (m1+m2) a = (m1+m2) g, звідки
Гирі будуть на одній висоті, коли кожна з них пройде відстань 0,5 м. З рівняння
Задача №2.Дано систему (рис.12), що складається з мас т1 = 50г і т2=30г, легкої пружинки та нерозтяжної і невагомої нитки. Система розглядається після загасання коливань пружини. Яким є рух цієї системи? Яка довжина пружини під час руху, якщо не навантажена пружина має довжину 10 см, а під дією сили 0,1Н видовжується на 2 см? При розв'язуванні цієї задачі не брати до уваги масу пружини, блока і його тертя. Розв’язування:При розв'язуванні деяких задач прискорення системи можна визначити зразу, знаючи результуючу діючих сил і (рис.12) масу системи. Так, за умовою цієї задачі дана система знаходиться під дією постійної сили F=(m1-m2)g, а тому рухається рівноприскорено. За другим законом динаміки F = та, де т = т1 + m2 — маса системи. Звідси
Після підстановки числових даних
Коли б дана пружина була підвішена нерухомо, то вона розтягалася б силою Р2 = т2×g. Якщо пружина разом з підвішеним до неї тягарем почне рухатися з прискоренням а = F' = m2 Результуюча сила розтягу F=P+F’=m2g+ Після підстановки значень одержимо
F= Видовження пружини, обумовлене цією силою,
Довжина пружини під час руху 10+7,4=17,4 (см).
Розв’язування. Оскільки відносно підлоги кошеня нерухоме, то діючі на нього сили взаємно зрівноважуються: з боку жердини на кошеня діє направлена вгору сила F, яка дорівнює вазі кошеняти mg. У відповідності з третім законом Ньютона на жердину діє сила F', яка дорівнює F, але напрямлена вниз. Тому другий закон Ньютона для руху жердини запишеться так: М×g + т×g = М×а, де а — прискорення жердини. Звідси
Задача№4.Ядро атома полонію Ро210 викинуло a- частинку з швидкістю 1600км/сек. Визначити швидкість віддачі ядра, що утворилося внаслідок a-розпаду ядра полонію. Розв’язування. За законом збереження кількості руху
Розв’язування. На тіло діє чотири сили (рис.14). Оскільки рух в нашому випадку здійснюється тільки вздовж вісі ОХ. Запишемо ІІ закон Ньютона. m×a=F+Fтр. Зробивши проекції на вісь ОХ і m×a=F–Fтр. (1) Fтр.=µ×N. За ІІІ законом Ньютона: N=m×g, тоді Fтр =µ×m×g (2) З рівняння (2) знайдемо силу: F=m×a+µ×m×g=m×(a+µ×g) (3) Так як тіло рухається рівноприскорено без початкової швидкості то прискорення рівне:
Підставивши (4) в (3) отримаємо кінцеву формулу для визначення сили:
Розв’язування.Направимо вісь ОХ вздовж похилої площини вниз, а вісь OY перпендикулярно площині в гору ( рис.15).. Запишемо ІІ закон Ньютона в проекціях на осі координат, ОХ:
Підставивши всі проекції а рівняння (1) отримаємо:
З рівняння (2) знайдемо прискорення:
Модуль сили N буде рівний:
Підставивши значення N в рівняння (3) отримаємо:
А якщо тертя відсутнє то прискорення буде рівне:
Задача№7. На горизонтальній гладкій поверхні розміщені три зв’язані друг з другом ниткою бруски масами m1, m2 i m3. На нитку, прикріплену до бруска масою m1 і перекинутій через нерухомий блок, прикріплено груз масою m4. Знайти прискорення цієї системи та силу натягу всіх ниток. Тертям в блоку знехтувати, масою блоку та нитками теж, а також врахувати, що нитки нерозтяжні.(. рис.16). F
Розв’язування: Сили які діють на тіла, показані на рис.16. Якщо тіла зв’язати між собою невагомою та нерозтяжною ниткою, то модуля сил натягу для кожної нитки рівні між собою і всі тіла рухаються з однаковим по модулю прискоренням. Виберемо осі координат. Напрям осі ОХ співпадає з напрямком руху тіл, ОY співпадає з напрямком прискорення а.
Розгленемо сили, які діють на кожне тіло окремо. Покажемо це на (рис.16а). Тоді T11= T1, T12 = T2, T13= T3, а1х=а2х=а3х=а4х=а.(1) Враховуючи рівність (1) запишемо ІІ закон Ньютона для кожного тіла окремо.
T3- Fтр3=m3×a, m4×g-T1 = m4×a Fтр=m×m×g Враховуючи те, що тіла рухаються по гладкій поверхні коефіцієнт тертя буде рівний нулю. Це означає, що сила тертя кожного із брусків буде теж рівна нулю оскільки сила тертя прямопропорційна коефіцієнту тертя. Тоді система рівнянь перепишеться без урахування сили тертя.
Додавши ці рівняння отримаємо:
m4g=(m1+m2+m3+m4)×a (3)
З (3) рівняння знайдемо прискорення:
Підставляючи рівняння (3) в систему рівнянь (1) починаючи з останнього знайдемо силу натягу ниток:
Задача№8. Через блок перекинута нитка, до кінців якої підвішені тягарці масою 2 кг та 2,1 кг. Початкова швидкість тягарців дорівнює нулю. Яке переміщення тягарців за час t =3c? Яка сила натягу нитки? Розв’язування: Сили які діють на тіла показано на рис.17. На рис 17а зображено рух кожного тягарця окремо. Враховуючи умову, що Т1=Т2=Т. Запишемо рівняння руху тягарців в проекціях на вісь OY яку спрямуємо за напрямком руху тягарця меншої маси. T-m1×g=m1×a, T-m2×g = -m2×a
Віднявши з першого рівняння друге отримаємо що: g×(m2-m1) = a×(m1+m2) Звідси;
Враховуючи, що тіла рухаються рівноприскорено без початкової швидкості запишемо рівняння для переміщення;
Підставивши замість прискорення його значення знайдемо кінцеву формулу для переміщення
Силу натягу нитки знайдемо з рівняння руху лівого тягарця
Задача№9.Два тягарця масою 4 кг та 1 кг зв’язані ниткою, яка перекинута через блок, який закріплено на вершині призми. Початкові швидкості тягарців рівні нулю. Знайти прискорення тягарців, якщо a=600, b=300, коефіцієнт тертя 0,2.(рис.18)
Запишемо ІІ закон Ньютона для кожного тіла окремо:
Віднявши від першого рівняння друге отримаємо вираз для прискорення:
Оскільки руху вздовж вісі OY не відбувається то можна записати рівняння ІІ закону Ньютона для двох тіл окремо:
Підставивши вирази сил реакції опори в рівняння (3) отримаємо:
а= 4,5 м/с2
|



 або а=2,45 м/сек2.
або а=2,45 м/сек2. визначимо
визначимо
 сек.
сек. Відповідь: 0,64с.
Відповідь: 0,64с.
 .
. , то пружину розтягатиме ще додаткова сила F, що надає масі m2 прискорення а. Отже,
, то пружину розтягатиме ще додаткова сила F, що надає масі m2 прискорення а. Отже,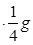
 ×g.
×g. кг
кг  Н.
Н.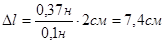
 Задача№3.Кошеня, що йде по підлозі, підстрибує і хапається за вертикальну жердину, підвішену за допомогою нитки до стелі. В цей момент нитка рветься. З яким прискоренням падає жердина, якщо кошеня піднімається по жердині так, що весь час знаходиться на одній і тій же висоті від підлоги? Маса кошеняти т, маса жердини М.(див. рис. 13)
Задача№3.Кошеня, що йде по підлозі, підстрибує і хапається за вертикальну жердину, підвішену за допомогою нитки до стелі. В цей момент нитка рветься. З яким прискоренням падає жердина, якщо кошеня піднімається по жердині так, що весь час знаходиться на одній і тій же висоті від підлоги? Маса кошеняти т, маса жердини М.(див. рис. 13)
 . Вважаючи ядро атома полонію до розпаду нерухомим і позначивши масу нового ядра М, а масу a-частинки т, можна записати
. Вважаючи ядро атома полонію до розпаду нерухомим і позначивши масу нового ядра М, а масу a-частинки т, можна записати
 Задача№5.Під дією сили F, спрямованої вздовж горизонтальної площини, по її поверхні починає ковзати тіло без початкової швидкості масою 4 кг через 3 с після початку руху набуває швидкості 0,6 м/с. Знайти силу F, якщо коефіцієнт тертя між тілом та площиною 0,2.
Задача№5.Під дією сили F, спрямованої вздовж горизонтальної площини, по її поверхні починає ковзати тіло без початкової швидкості масою 4 кг через 3 с після початку руху набуває швидкості 0,6 м/с. Знайти силу F, якщо коефіцієнт тертя між тілом та площиною 0,2. запишемо другий закон в скалярній формі:
запишемо другий закон в скалярній формі:
 (4).
(4).

 Задача№6 На похилій площині з кутом нахилу aсковзає вниз брусок масою m. Знайти його прискорення, якщо коефіцієнт тертя бруска з поверхнею m.
Задача№6 На похилій площині з кутом нахилу aсковзає вниз брусок масою m. Знайти його прискорення, якщо коефіцієнт тертя бруска з поверхнею m. (1)
(1) ;
;

 (2)
(2) (3)
(3)

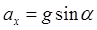


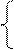 Т1-Т2-Fтр1=m1×a, T2-T3- Fтр2=m2×a (2)
Т1-Т2-Fтр1=m1×a, T2-T3- Fтр2=m2×a (2) (2)
(2) (4)
(4)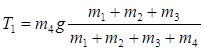 ;
; 
 .
.
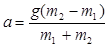


 .
. ,
, .
. Розв’язування. На малюнку показані сили, а також вибрані системи координат для кожного тіла відповідно. Також з малюнку видно що перше тіло рухається вздовж вісі ОХ, а друге тіло вздовж вісі О¢Х¢, також врахуємо, що Т=Т¢
Розв’язування. На малюнку показані сили, а також вибрані системи координат для кожного тіла відповідно. Також з малюнку видно що перше тіло рухається вздовж вісі ОХ, а друге тіло вздовж вісі О¢Х¢, також врахуємо, що Т=Т¢ ;
;  ;
; 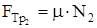 .
. (1)
(1) (2)
(2) (3)
(3) ,
, 

 (4)
(4)