 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приклади розв'язування задач
КІНЕМАТИКА 1. Прямолінійний рівномірний рух
2. Прямолінійне рівноприскорений рух ( сповільнення)
а u=u0+а×t (4)
Якщо u0=0 то
3. Вільне падіння тіла.
u=-u0+g×t (10) u=-u0+g×t (13)
4. Рух тіла кинутого вертикально вгору
Максимальна висота підьому знайдемо з рівняння (17)
Щоб знайти час підьому, необхідно використати умову, що швидкість в точці В uв=0. Тоді з виразу (16) отримаємо
5. Рух тіла по колу.
1) дотичного прискорення ат спрямованого по дотичній до кола; 2) доцентрованого прискорення яке чисельно рівне
та спрямоване до центру кола. Загальне прискорення рівне
Дотичне прискорення ат характеризує зміну швидкості по величині . Якщо рух тіла рівномірний, то ат =0, пройдений шлях, тобто дуга, знаходиться за формулою (2). Якщо рух прискорений або сповільнений, то використовуються формули (3)-(6), де замість прискорення а потрібно писати ат. Доцентрове прискорення характеризує зміну швидкості по напрямку. 6. Рух тіла кинутуго під кутом до горизонту
uОx=u0cosa0 (23) uОy =u0sin a0 (24)
ux=u0cosa; (26) uy=u0sina-gt. (27)
В точці В Використовуючи рівність (23),з (26) знайдемо час підьому 0=u0sina-gt1 Þ Час польоту Т=2×t1 (32) Дальність польоту L=u0х×Т (33) Висота підьйому 7. Складний рух точки
Якщо u1 ^ u2 тоді
Якщо u1 ║ u2 тоді
Приклади розв'язування задач
Розв’язування: Коли б літак летів у тиху погоду, то його швидкість вздовж меридіана дорівнювала б:
Абсолютне значення швидкості літака знаходимо за теоремою косинусів
Підставивши числові значення величин в одиницях СІ, дістанемо: u = Для визначення курсу літака відносно меридіана, тобто для визначення кута
Відповідь: u = 143,26 м/с; g= 3026’ Задача 2.Кінематичне рівняння руху матеріальної точки по прямій (вісь х) мас вигляд х=А+Вt+Сt3, де А=4 м, В=2 м/с, С=0,5 м/с3. Для моменту часу t1=2с визначити: 1) координату точки х1; 2) миттєву швидкість u1; миттєве прискорення Розв’язування.1. Визначимо координату точки, якщо в рівняння руху підставимо значення часу: х1 = А + Bt + Ct Підставляючи числові значення А, В, С, t1. в рівність (1) знаходимо: що x1=4м.. 2. Знаходимо миттєву швидкість у довільний момент часу:
Тоді в момент часу t1 миттєва швидкість u1= B + Ct Підставляючи числові значення В, С, t1 в рівність (2) одиницях СІ і, виконуючи обчислення, знаходимо: u1 = - 4м/с Від'ємне значення u1показує, що в момент часу t1 = 2с точка рухається в протилежному напрямі відносно координатної осі. 3.Миттєве прискорення в довільний момент часу знайдемо, взявши другу похідну від координати х:
Миттєве прискорення в момент часу t1:
Підставивши у формулу (3) числові значення величин С, t1, знайдемо, що митєве прискорення буде:
Від'ємне значення а показує, що напрямок вектора прискорення протилежний напряму координатної осі. Відповідь: х1= 4 м; u1= -4 м/с;
Задача 3 Тіло кинуте під кутом Розв’язування. Виберемо систему координат з початком в точці кидання тіла, вісь OY спрямуємо вертикально в гору, ОХ – горизонтально, в ту сторону, куди кинуто тіло ( рис.2)
Запишемо початкові умови: х0 = 0, y0 = 0 uОx=u0cosa0 uОy =u0sin a0 Значення проекцій прискорення на осі координат рівні: ах=0, аy=-g. Залежність проекцій швидкостей від часу запишемо в такому вигляді: ux=u0cosa; uy=u0sina-gt. З трикутника швидкостей знайдемо модуль та напрямок вектора швидкості в будь – який момент часу.
Напрямок вектора швидкості:
Координати тіла в момент часу t рівні:
Час польоту tп та максимальну висоту підйому легко знайти, якщо звернути увагу на те, що вздовж вісі OY тіло рухається вертикально вгору з початковою швидкістю uoy, модуль якої рівний uoy = u0sina. Час польоту, це час до падіння тіла на Землю, в момент падіння координата тіла „y” буде рівна нулю. Тоді з рівняння (4) можна знайти час польоту тіла.
Час t1підйому тіла на максимальну висоту можна знайти слідуючим чином. Проекція швидкості на вісі Y змінюється за законом uy=u0Y-gt = u0sina0- gt. В точці „В” (найвищій точці польоту) проекція швидкості буде рівна uвy=0. Тоді
З цього виразу знайдемо час підйому тіла на максимальну висоту t1:
Порівнявши формули (5) і (5а) встановлюємо, що час підйому в половину менший за час польоту тіла, а це означає, що час підйому тіла і час падіння тіла однакові. Якщо в вираз (4) підставитьи вираз (5а), то знайдемо максимальну висоту підйому:
Якщо у вираз (3) підставити час польоту тіла tп (вираз (5)), то цим самим знайдемо дальність польоту тіла: Враховуючи, що в момент падіння t = tn , то з рівняння переміщення, можа знайти дальність польоту S в горизонтальному напрямку.
S = (u0cosa0)tn = u0cosa0 З отриманого результату можна зробити висновок, що при заданій швидкості u0, найбільша дальність буде тоді, коли sin 2a0 = 1, тобто при куті кидання 450. При цьому
Smax =
Модуль і напрям вектора швидкості u1 в момент падіння найдемо, підставивши значення tn із формули (5) в формулу (1) і в формулу (2).
Таким чином, модуль швидкості тіла в момент падіння рівний модулю початкової швидкості і Для того, щоб отримати рівняння траєкторії руху тіла, потрібно виключити час t з рівнянь (3) та (4). Знайдемо час t з рівняння (3)
Отримане рівняння підставимо в рівняння (4). Маємо
З математики відомо, що функція у = ах2 + bх при а < 0 є парабола, яка проходить через початок координат, та орієнтована випуклістю вгору. Таким чином тіло, кинуте під кутом до горизонту, рухається по параболі.
Задача № 4 Два тіла рухаються рівномірно назустріч одне одному і відстан між ними зменшується на S = 16 м за кожний t = 10с. Якщо ці тіла, з такими ж за величиною швидкостями, будуть рухатися в одному напрямі, то відстан між ними збільшується на S1 = 3 м за кожні t1 = 5с. З якою швидкістю рухається кожне з цих тіл? Розв’язування: В першому випадку при русі тіл назустріч одне одному відстань S становить шлях, пройдений обома тілами разом за час t, тобто
в другому випадку оскільки одне з тіл має більшу швидкість, відстань між ними збільшується за час t1, на величину S1. Отже можна записати:
S1=u×t1 - u1×t1=t1×(u+u1) (2) Перепишемо рівняння (1) та (2) в систему:
Додаючи праві і ліві частини рівнянь, одержимо:
Так само знаходимо значення u1
Після підстановки числових даних маємо : u1 = 0,5 м/с Відповідь: u= 1,1 м/с; u1 = 0,5 м/с Задача № 5. Два автобуси одночасно виїхали з пункту А в пункт В. Один з них першу половину шляху проїхав з постійною швидкістю u1, а другу половину шляху з постійною швидкістю u2. Другий автобус їхав з швидкістю u1 половину всього часу свого руху від А до В, а другу половину часу – з швидкістю u2. Визначити середню швидкість руху кожного автобуса, якщо u1=30 км/год. і u2=50 км/год. Розв’язування: Середня швидкість визначається відношенням всього пройденого шляху до всього затраченого часу. Зробимо схематичний малюнок на якому зображемо рух тіла (див. рис.3).
де S – повний шлях; t – повний час.
Для першого автобусу весь пройдений шлях буде: S=S1+S2; оскільки за умов задачі S1=S2, тоді S=2S1. (2)
Весь час буде рівний t = t1+t2, де
Підставивши (2), (3) в (1) отримаємо:
Після підстановки отримаємо, що uср1.=37,5 км/год. Для другого автобусу запишемо:
Весь час рівний: t=t1+t2, але за умов задачі отримаємо що t1=t2 тобто t=2t1 (5) Весь пройдений шлях рівний : S=S1+S2 де.
Тоді S=t1(u1+u2) (6) Підставивши в (4) рівняння (5) та (6) отримаємо:
Відповідь: uср1=37,5 км/год, uср2=40 км/год Задача №6.Весь шлях автомобіль проїхав із середньою швидкістю 80км/год. Середня швидкість на першій чверті шляху дорівнювала 120 км/год. Яка була середня швидкість на решті шляху ? Розв’язування: Середня швидкість визначається відношенням всього пройденого шляху до всього затраченого часу. Зробимо схематичний малюнок на якому зображемо рух тіла (див. рис.4).
де uср=80км/год. Весь шлях рівний S=S1+S2 де S1=1/4S, S2=3/4S. Весь час t=t1+t2, де
Підставивши значення t1, t2 в t маємо:
Підставивши (2) в (1) отримаємо;
З останього виразу знайдемо u2:
Підставивши дані отримаємо, що uср2 = 72 км/год Задача №7.Ескалатор метрополітену піднімає пасажира, що стоїть на ньому нерухомо, за 1 хв. По нерухомому ескалатору пасажир піднімається за 3хв. За який час пасажир піднімається по рухомому ескалатору? Розв’язування:Запишемо рівняння руху для кожного з випадків вказаних в умові задачі.
де S –довжина ескалатора, u1- його швидкість, u2- швидкість руху пасажира по нерухомому ескалаторі, t1- час підіймання нерухомого пасажира ескалатором, t2 – час підіймання пасажира по нерухомому ескалаторі, t3 – шуканий час підіймання рухомого пасажира по рухомому ескалаторі. Знайшовши швидкості з першого та другого рівняннь
та підставивши їх в третє, отримаємо:
звідси
Відповідь: t3=45c.
Розв’язування: Середня лінійна швидкість супутника визначається формулою:
де S – шлях який пройшов супутик, зробивши повний оберт, Т- час одного повного оберту супутника. Шлях супутника, це довжена кругової орбіти з радіусом обертання (R+h).Тобто S=2p×(R+h). Т-період обертання який становить, Т=6300с. Підставивши значення шляху та часу в формулу середньої швидкості будемо мати:
Кутова швидкість прирівномірному русі;
Якщо супутник зробив один оберт то кут повороту рівний j=2p рад, а час буде рівний періоду обертання t=Т. Тоді
Відповідь:
Задача №9.На горизонтальній вісі обертаються зі швидкістю 3000об/хв два тонких диски, закріплених на відстані S=100см один від одного. Пущена паралельно вісі куля пробиває обидва диски, причому друга пробоїна виявилась зміщеною відносно першої на кут 450. Пробивши диски, куля заглиблюється в мішень на d=60 см. Знайти: 1.) швидкість кулі під час руху її між дисками, вважаючи швидкість постійною; 2.) час руху в мішені; 3.) прискорення в мішені.
Розв’язування: Швидкість буде рівна
де S шлях між дисками, t – час руху між дисками. Під час руху кулі між дисками вони повертаються на 450 або на де Т період обертання дисків який визначається
де n- частота обертання. n=3000об/хв=50 об/сек. Підставивши всі перетворення в формулу (1) маємо;
Прискорення руху кулі в мішені можна визначити за формулою
звідки Тоді час руху в мішені можна знайти з рівняння закону зміни швидості при прискореному русі:
З цього рівняння знайдемо час руху кулі в диску. Маємо
Задача № 10.Літак знижується на ціль під кутом 60 до горизонту зі швидкістю 540км/год і кидає бомбу на висоті 600м. На якій відстані від цілі в горизонтальному напрямі потрібно звільнитися від бомби, щоб вона вразила ціль? Опором повітря знехтувати.
Випишемо початкові умови: х0=0, y0=0, u0x=u0cosa, u0y=u0sina. Залежність координати бомби від часу запишемо рівнянням:
Бомба потрапляє в ціль в момент часу t=t1 при цьому y=h, S=x. Враховуючи це, на основі рівняння (2) отримаємо висоту;
З рівняння висоти знайдемо час падіння бомби:
При вирішенні квадратного рівняння другий корінь одержується від’ємний тому фізичного змісту немає. Підставивши t1 в рівняння (1) знайдемо відстань від цілі в горизонтальному напрямі:
Підставивши числові значення, отримаємо
Задача №.11 Тіло кинуто з початковою швидкістю u0 під кутом a0 до похилої поверхні, яка утворює з горизонтом кут b. Визначити час польоту та максимальне віддалення тіла від похилої поверхні. Розв’язування: За початок відліку приймемо точку кидання тіла, вісь ОХ спрямуємо вздовж похилої поверхні, вісь ОY перпендикулярно ОХ (див.рис.8). Випишемо початкові умови: х0=0, y0=0,u0x=u0×cosa0,u0y=u0sina0, також знайдемо проекції прискорення на осі координат; ax=gx=g×sinb, ay=gy=g×cosb.
Рух тіла можна розглянути як результат складання двох прямолінійних рухів: рівноприскорений рух вздовж осі ОХ з прискоренням gx, та рівнозміний рух вздовж осі OY з прискоренням gy. Значення проекцій швидкостей в момент часу t: uх=u0х+ах×t uy=u0y+ay×t. Координати тіла в момент часу t:
Підставимо отримані рівняння u0х, u0y, аx, аy в рівняння швидкостей та координат держимо:
Час польоту знайдемо з рівняння тієї координати яка в момент падіння буде рівна нулю. Такою координатою виступатиме координата „у”. Запишемо умову:
Після вирішення рівняння отримаємо:
Враховуючи, що в момент падіння координата х=S, тоді дальність польоту знайдемо з рівності (3), враховуючи час польоту :
Після перетворення одержимо:
Для знаходження максимального віддалення тіла від похилої поверхні в рівняння (4) підставимо значення часу підйому t2, який знайдемо з рівності (2) де врахуємо , що в найвищій точці траєкторії проекція швидкості на вісь OY буде рівна нулю.
Звідси маємо
Тоді, враховуючи, що в цій точці y=h, отримаємо
Після перетворень отримаємо,
Розв’язування: Зробимо схематичний малюнок на якому зображено рух потягів один відносно іншого. Зв’яжемо рухому систему відліку з першим потягом, за початок координат О¢ візьмемо місцезнаходження пасажира. За додатній напрям осі О¢Х¢ візьмемо напрям руху другого потягу. Нерухома система відліку пов’язана з землею (рис.9). Згідно закону складання швидкостей запишемо;
де u2¢ - швидкість другого потягу відносно першого. З першої рівності,
Знайдемо проекцію вектора
Координата другого потягу в момент часу буде
В момент часу t=t1, коли останій вагон другого потягу проходить повз пасажира, то х¢=0, тобто з рівняння координати можна знайти довжину потягу,
З цієї рівності маємо,
Задача №14.В морі два кораблі рухаються зі швидкостями Розв’язування: Зробимо схематичний малюнок в якому, рухому систему X¢O¢Y¢ пов¢яжемо з первим кораблем прийнявши за додатній напрямок вісь О¢Х¢ , тобто напрямок швидкості першого корабля (рис.10). нерухому систему координат XOY пов’яжемо з водою. В системі X¢O¢Y¢ другий корабель рухається зі швидкістю u2¢. Згідно закону складання швидкостей запишемо:
В проекціях на вісі координат О¢Х¢ і O¢Y¢ отримаємо:
Знаючи проекції векторів
Напрям вектора u2¢ визначається кутом b, який рівний
ДИНАМІКА Другий закон Ньютона
m- маса точки в (кг);
Сила – це міра взаємодії між двома тілами. Сила тяжіння Землі спрямована вертикально вниз; Вага сила яка прикладена до опори; Сила тертя де m- коефіцієнт тертя, а N реакція опори площини, спрямована вертикально догори.
Сила тертя спрямована в протилежну сторону швидкості.
Сила пружності.
Fпр – сила пружності, в протилежну сторону зміщенню. к- коефіцієнт жорсткості пружини(Н/м); L0- довжина недеформованої пружини; х- зміщення пружини(м). Імпульс тіла(кількість руху).
Імпульс тіла направлений по напрямку швидкості.
Закон збереження імпульсу системи двох тіл:
де u1, u2- швидкості тіл 1 та 2 до взаємодії, відповідно u1, u2- швидкості тіл 1 та 2 після взаємодії. |




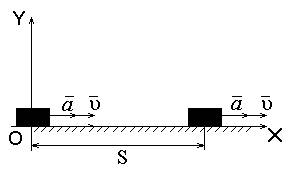 а= const
а= const (3)
(3)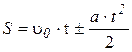 (5)
(5)
 (6)
(6) u=а×t (7)
u=а×t (7) (8)
(8)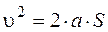 (9)
(9)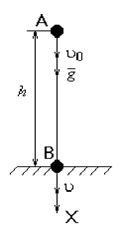
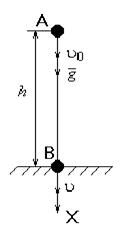 u0- спрямоване вниз u0- спрямоване вниз
u0- спрямоване вниз u0- спрямоване вниз (11)
(11)  (14)
(14) (12)
(12)  .(15)
.(15) u=-u0 – g×t (16)
u=-u0 – g×t (16)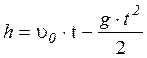 (17)
(17) (18)
(18) (19)
(19) (20)
(20) Повне прискорення а складається з двох прискорень:
Повне прискорення а складається з двох прискорень: (21)
(21) (22)
(22)
 х=u0х×t (25)
х=u0х×t (25) (28)
(28)
 (31)
(31)
 (35)
(35) (36)
(36) (37)
(37) (38)
(38) Якщо u1 не ^ u2 тоді
Якщо u1 не ^ u2 тоді  (39)
(39) u=u1-u2 (40)
u=u1-u2 (40)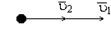 u=u1+u2
u=u1+u2 Задача 1.З якою швидкістю uповинен летіти та якого курсу повинен триматися літак відносно меридіана, щоб за час 0,5 год він пролетів у північному напрямі шлях 248,4 км, якщодує північно-східний вітер під кутом 60° до меридіана зі швидкістю 36км/год?
Задача 1.З якою швидкістю uповинен летіти та якого курсу повинен триматися літак відносно меридіана, щоб за час 0,5 год він пролетів у північному напрямі шлях 248,4 км, якщодує північно-східний вітер під кутом 60° до меридіана зі швидкістю 36км/год? Але оскільки літак під час польоту зноситься вітром у південно-західному напрямі зі швидкістю u1, то його швидкість вздовж меридіана u2 відрізняється від шуканої швидкості літака, яка дорівнює u =u2 – u1(див. рис.1)
Але оскільки літак під час польоту зноситься вітром у південно-західному напрямі зі швидкістю u1, то його швидкість вздовж меридіана u2 відрізняється від шуканої швидкості літака, яка дорівнює u =u2 – u1(див. рис.1)
 =143.26м/с
=143.26м/с , скористаємось теоремою синусів
, скористаємось теоремою синусів , звідки
, звідки  ;
; ;
;  = 3026’
= 3026’ 1.
1. .(1)
.(1) (2)
(2)

 (3)
(3)

 За початок відліку часу візьмемо момент кидання тіла. В цій системі координат рух тіла можна розглянути, як результат складання двох прямолінійних рухів: рівномірного руху вздовж осі ОХ зі швидкістю uОХ, та кинутого вертикально вгору з початковою швидкістю uОy, вздовж осі OY.
За початок відліку часу візьмемо момент кидання тіла. В цій системі координат рух тіла можна розглянути, як результат складання двох прямолінійних рухів: рівномірного руху вздовж осі ОХ зі швидкістю uОХ, та кинутого вертикально вгору з початковою швидкістю uОy, вздовж осі OY. (1)
(1) (2)
(2) (3)
(3) (4)
(4)
 (5)
(5)
 (5а)
(5а)
 . (6)
. (6) ;
; 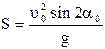 (7)
(7)
 ; (8)
; (8) .
.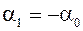 . Кут падіння
. Кут падіння  .
. ,
,




 , (1)
, (1)
 ,
,  , тоді
, тоді ; (3)
; (3)

 ,
,


 . (2)
. (2)
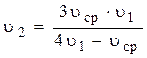 .
. ; (1)
; (1) ; (2)
; (2) . (3)
. (3) ,
,  ,
, ,
,

 Задача №8.Визначити середою лінійну і кутову швидкість третього радянського штучного супутника Землі, якщо період його обертання по орбіті становив 105 хв, а середня висота польоту 1200 км? Радіус Землі R=6400 км.на рис. 5 зображено рух супутника на орбіті..
Задача №8.Визначити середою лінійну і кутову швидкість третього радянського штучного супутника Землі, якщо період його обертання по орбіті становив 105 хв, а середня висота польоту 1200 км? Радіус Землі R=6400 км.на рис. 5 зображено рух супутника на орбіті.. ,
,


 ,
,  рад/с.
рад/с. На рис 6. зображено рух кулі між дисками, а також показано зміщення кулі в другому диску.
На рис 6. зображено рух кулі між дисками, а також показано зміщення кулі в другому диску. , (1)
, (1) оберта. Тоді час руху між дисками буде рівний t =
оберта. Тоді час руху між дисками буде рівний t =  ,
,
 , u02=0, d-шлях який куля пройшла в другому диску. Знак мінус показує, що рух сповільнений. Тоді маємо
, u02=0, d-шлях який куля пройшла в другому диску. Знак мінус показує, що рух сповільнений. Тоді маємо
 .
. ,
,
 ;
;  ; t
; t  0.003 сек.
0.003 сек. Розв’язування.Виберемо систему координат так як показано на рис.7.
Розв’язування.Виберемо систему координат так як показано на рис.7. (1)
(1) . (2)
. (2)

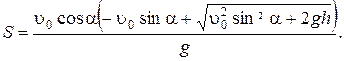


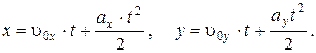
 (1)
(1)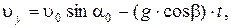 (2)
(2) (3)
(3) (4)
(4) (5)
(5)






 Задача № 12.Два потяги їдуть на зустріч один одному зі швидкостями u1=12м/c і u2=18м/с. Пасажир в першому потязі помічає, що другий потяг проїжджає повз нього за час 8с. Яка довжина другого потягу.
Задача № 12.Два потяги їдуть на зустріч один одному зі швидкостями u1=12м/c і u2=18м/с. Пасажир в першому потязі помічає, що другий потяг проїжджає повз нього за час 8с. Яка довжина другого потягу.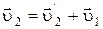 ;
; .
. на вісь О¢Х¢:
на вісь О¢Х¢:
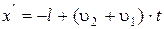
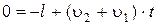

 Підставивши числові значення отримаємо, що довжина другого потягу дорівнює l=240м.
Підставивши числові значення отримаємо, що довжина другого потягу дорівнює l=240м. під кутом a один до одного. Знайти швидкість другого корабля відносно першого.
під кутом a один до одного. Знайти швидкість другого корабля відносно першого. .
. , знайдемо модуль швидкості
, знайдемо модуль швидкості

 (1)
(1) -вектор прискорення точки (м/с2);
-вектор прискорення точки (м/с2); - сили, які діють на точку(Н);
- сили, які діють на точку(Н); (2)
(2) (3)
(3) (4)
(4)
 (5)
(5)  (7)
(7) (6)
(6) 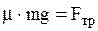 (8)
(8)
 (9)
(9) (10)
(10) Теорема: Зміна кількості руху за деякий проміжок часу рівний імпульсу сили.
Теорема: Зміна кількості руху за деякий проміжок часу рівний імпульсу сили.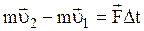 (11)
(11) (12)
(12)