 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Модифицированный метод Ньютона
При поиске экстремума неквадратных функций метод Ньютона не очень надежен, при неудачном выборе начального приближения шаг поиска окажется слишком большим и итерации не сойдутся. Для устранения этого недостатка используют модифицированный метод Ньютона. Он реализуется такими итерациями:
Коэффициент Метод эффективный и надежный, если вычисление первых и вторых производных не связано с трудностями. Недостаток состоит в необходимости построения и решения линейного уравнения, содержащего элементы матрицы Гессе (для вычисления Метод Марквардта Метод Марквардта (1963 г.) является комбинацией методов Коши и Ньютона, сочетает положительные свойства обоих методов. Итерации выполняются по формуле
Направление поиска на каждой итерации определяется как
где В начале поиска значение
и направление поиска:
Если после первого шага получается точка с меньшим значением целевой функции Преимущества алгоритма: простота, высокая скорость сходимости в окрестности минимума Недостаток алгоритма: необходимость вычисления матрицы Гессе и обращения матрицы Метод хорошо работает в задачах с целевой функцией вида
(например, задачи регрессионного анализа). Квазиньютоновские методы Квазиньютоновские методы оптимизации обладают положительными чертами метода Ньютона, но используют только первые производные. Все квазиньютоновские методы используют итерационную процедуру (4.1), в которой направление поиска задается в виде
где
где Метод Дэвидона-Флетчера-Пауэлла (ДФП). Один из наиболее широко применяемых градиентных методов – метод Дэвидона-Флетчера-Пауэлла (ДФП). Используются следующие обозначения
Упрощенно алгоритм можно представить такими шагами 1. Задать начальную точку 2. Минимизировать 3. Вычислить 4. Обновить метрику
5. Вычислить 6. Если не выполнены условия окончания поиска, то присвоить 7. Конец алгоритма. Метод ДФП использует идеи метода Ньютона-Рафсона и свойство сопряженных направлений. Для минимизации квадратичной функции |



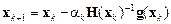 ,
, 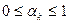 .
. (параметр шага) выбирают на каждом шаге так, чтобы
(параметр шага) выбирают на каждом шаге так, чтобы  , (как в методе Коши), это гарантирует, что
, (как в методе Коши), это гарантирует, что  .
. .
. ,
,
 – матрица Гессе;
– матрица Гессе;  – единичная матрица.
– единичная матрица. >>1 (например,
>>1 (например,  ), тогда
), тогда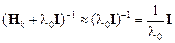 ,
, .
.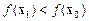 , следует выбрать
, следует выбрать  <
<  и продолжить. Иначе принять
и продолжить. Иначе принять  ,
,  и вновь реализовать предыдущий шаг.
и вновь реализовать предыдущий шаг. .
. .
.
 ,
, – положительно определенная симметрическая матрица, которая называется метрика. Матрица
– положительно определенная симметрическая матрица, которая называется метрика. Матрица  ,
, – корректирующая матрица, и в пределе становится равной обратному гессиану.
– корректирующая матрица, и в пределе становится равной обратному гессиану. ,
,  или
или 
 и начальную матрицу
и начальную матрицу  (обычно единичная матрица)
(обычно единичная матрица)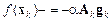
 .
.
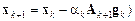
 , перейти на 2.
, перейти на 2. переменных метод ДФП сходится не более чем за
переменных метод ДФП сходится не более чем за