 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сжатие, использующее точку С
Если значения функции в точках R и W одинаковы, следует проверить другую точку. Возможно, значение функции меньше в точке М, но нельзя заменять вершину W точкой М, так как три точки должны составлять треугольник. Рассмотрим две средние точки С1 и С2, которые лежат на отрезках WM и MR соответственно (рис. 4.3).
Рис. 4.3. Сжатие точки С1 или С2 для метода Нелдера-Мида Точку, в которой функция принимает наименьшее значение, обозначаем через С и получаем новый треугольник BGC. Сокращение по направлению к В Если значение функции в точке С не меньше, чем значение в W, точки G и W следует "стянуть" к точке В (рис. 4.4).
Рис. 4.4. Сокращение треугольника к точке В
Точку G заменяем точкой M, a W – точкой S, которая является средней точкой на отрезке, соединяющем точки В и W. Численно эффективный алгоритм будет вычислять функцию только при необходимости. На каждом шаге находим новую вершину, которой заменяем вершину W. После ее нахождения в дальнейшем исследовании не будет необходимости и шаг итерации будет завершен. Алгоритм Нелдера-Мида 1. Задать начальный симплекс, вычислить значения ЦФ в вершинах симплекса, выбрать вершины B, W, G. 2. Если выполнены условия окончания поиска, то объявить точку B минимумом и перейти на 500 3. Выполнить операцию отражения для получения вершины R. 4. Если f(R) < f(G), то перейти на 5 (отражение, либо растяжение) Иначе перейти на 6 (сжатие либо растягивание) 5. Если f(B) < f(R) то заменить W на R, иначе вычислить Е и f(E), Если f(E) < f(B) то замена W на Е иначе замена W на R. Перейти на 2 6. Если f(R) < f(W) то замена W на R Вычислить С = (М+ R)/2 или С = (М+ R)/2 и f(С) Если f(С) < f(W) то замена W на С иначе вычислить S и f(S) замена W на S, замена G на M Перейти на 2. 7. Конец алгоритма Поиск минимума ЦФ завершается, когда размеры симплекса или разность между значениями в вершинах симплекса становятся достаточно малыми. Часто используют дисперсия
где
Выполнение условий окончания поиска Основным преимуществом симплексного метода является возможность работы с большим симплексом, т. е. сильно разнесенными точками. Это помогает избежать сжатия симплекса в точке локального минимума. Симплексный метод предпочтителен при выявлении области минимума функции ошибок, т. е. начального приближения к точке минимума при переходе к другим методам оптимизации. Метод Хука-Дживса Данный метод один из наиболее простых прямых методов поиска (1960 г). Метод использует попеременно исследующий (зондирующий) поиск и поиск по образцу (модельный ход). 1. Исследующий поиск позволяет из текущей точки 2. После определения направления от точки Алгоритм Хука-Дживса 1. Ввести начальные значения: 2. Вычислить значение ЦФ в базисной точке
3. Выполнить исследующий поиск в точке 4. Если 5. Выполнить поиск по образцу, используя новую базисную точку
6. Выполнить исследующий поиск в т. 7. Если 8. Если 9. Закончить поиск, печатать результаты. Окончание поиска происходит при условии, что длина шагов Исследующий поиск метода Хука-Дживсасодержит такие шаги: 1. Вход: базисная точка Задать начальное значение счетчика итераций k = 1 и начальное значение шага переменой h. 2. Увеличить координату
Вычислить значение функции 3. Если 4. Уменьшить координату на шаг
5. Если 6. Если не достигнуто уменьшения ЦФ, оставить 7. Запомнить новые значения 8. Если не все переменные использованы, т.е. 9. Конец исследующего поиска. Получена новая базисная точка Достоинства алгоритма Хука-Дживса: - используются простые операции, не приводящие к запрещенным арифметическим действиям (типа деления на 0); - не высокие требования к памяти компьютера Недостатки алгоритма: - исследующий поиск выполняется только в направлении осей координат, что может привести к прекращению поиска без достижения минимума, если направление «оврага» не параллельно осям координат; - большое количество вычислений целевой функции. В этом случае при выполнении условия окончания поиска целесообразно выбрать другую начальную точку и повторить поиск минимума. Решение можно считать найденным при совпадении минимумов. Окончание поиска по методу Хука-Дживса происходит при длине шагов |






 – значения ЦФ в вершинах симплекса,
– значения ЦФ в вершинах симплекса,  – среднее значение ЦФ в вершинах симплекса
– среднее значение ЦФ в вершинах симплекса .
. соответствует либо малому ребру симплекса, либо попаданию стационарной точки внутрь симплекса, либо одновременному выполнению обоих условий.
соответствует либо малому ребру симплекса, либо попаданию стационарной точки внутрь симплекса, либо одновременному выполнению обоих условий. пространства выбрать направление, движение в котором обеспечивает минимизацию целевой функции.
пространства выбрать направление, движение в котором обеспечивает минимизацию целевой функции. – шаг изменения переменной;
– шаг изменения переменной;  - минимальное значение шага;
- минимальное значение шага;  < 1 – константа изменения длины шага
< 1 – константа изменения длины шага
 и значение ЦФ в этой точке,
и значение ЦФ в этой точке,  .
. (значение ЦФ уменьшилось), перейти на => 8
(значение ЦФ уменьшилось), перейти на => 8 .
. , получить точку
, получить точку  и значение ЦФ
и значение ЦФ  .
.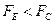 , определить новую базисную точку: присвоить
, определить новую базисную точку: присвоить  ;
;  ;
; 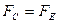 , перейти на => 5.
, перейти на => 5. , то уменьшить длину шага,
, то уменьшить длину шага,  , перейти на => 3.
, перейти на => 3.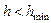 (минимального заданного значения)
(минимального заданного значения) , значение ЦФ
, значение ЦФ  на шаг
на шаг  :
: (для k =1 будет
(для k =1 будет  )
)
 , перейти на => 7
, перейти на => 7 (для k = 1
(для k = 1  )
) , перейти на => 7
, перейти на => 7 без изменений, и перейти на => 8.
без изменений, и перейти на => 8.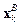 и
и  .
. , то перейти к следующей переменной,
, то перейти к следующей переменной,  , и перейти на => 2, иначе закончить поиск, перейти на => 9
, и перейти на => 2, иначе закончить поиск, перейти на => 9 .
. . Если значение ошибки (целевой функции) не удовлетворяют проектировщика, то можно повторить процесс оптимизации, задав новые значения компонентов или модифицировать принципиальную схему для получения желаемого результата.
. Если значение ошибки (целевой функции) не удовлетворяют проектировщика, то можно повторить процесс оптимизации, задав новые значения компонентов или модифицировать принципиальную схему для получения желаемого результата.