 ПОЗНАВАТЕЛЬНОЕ
| Общая постановка транспортной задачи.
Транспортная задача является одной из важнейших частных задач линейного программирования. Название свое задача получила потому, что впервые была сформулирована и поставлена для решения вопроса о наиболее рациональном планировании перевозок на транспорте. Название это условно, так как с ее помощью можно решать разнообразные задачи из различных отраслей производства и не обязательно связанных с перемещением. Методы решения транспортной задачи широко применяют на автомобильном, железнодорожном и других видах транспорта для планирования перевозок различных грузов. Это объясняется их простотой и экономическим эффектом, который они дают. Планы перевозок, разработанные на основе алгоритма транспортной задачи, как правило, на 12—18% экономичнее планов, составленных без применения математических методов. В лесной, целлюлозно-бумажной и деревообрабатывающей промышленности транспортирование составляет значительную часть производственного процесса: трелевка древесины, вывозка на промежуточные и нижние склады, доставка па деревообрабатывающие предприятия, междуцеховые и внутрицеховые перемещения на нижних складах и так далее. Транспортные расходы занимают значительный удельный вес в общей структуре лесозаготовок, вот почему задача оптимального планирования работы транспорта является одной из основных задач, решаемых методами математического программирования. Классическая транспортная задача линейного программирования — это задача о наиболее экономичном плане перевозок однородных или взаимозаменяемых грузов из пунктов производства в пункты потребления или, что тоже самое, это задача об оптимальном прикреплении потребителей к поставщикам. Сформулируем транспортную задачу. В лесозаготовительном объединении имеются А1, А2, ... ..., Аm лесозаготовительных предприятий {ЛЗП), вырабатывающих технологическую щепу в объеме Q1, Q2, .... Qm тысяч кубометров в год. Технологическая щепа должна быть доставлена потребителям (ЦБК) В1, В2, ….., Вn, имеющим соответственно объемы потребления Y1, Y2. … Yn тысяч кубометров в год. Стоимость доставки щепы с каждого ЛЗП каждому потребителю определяется матрицей стоимостей:
Объем выработки щепы всеми ЛЗП равен объему потребления всеми ЦБК:
или
Необходимо определить такое распределение доставки щепы от ЛЗП к потребителям, чтобы общая стоимость транспортных затрат была минимальной:
или
При этом необходимо, чтобы соблюдались условия: 1. Суммарный объем щепы, вывозимой с каждого ЛЗП потребителям, должен равняться его мощности:
или
где i=1,2,……m. 2. Суммарный объем щепы, доставляемой на каждый ЦБК от ЛЗП, должен равняться его потребности:
или
где j=1,2,……n. 3.Объемы доставки щепы не могут быть отрицательными, но могут равняться нулю:
4.Уже известное (1.3)
Математически сформулированная транспортная задача линейного программирования имеет m+n+2 уравнений, и m·n+1 неизвестных. Кратко транспортная задача линейного программирования записывается в следующем виде. Найти минимум функции
При заданных условиях:
Функция функционалом. Решение задачи сводится к нахождению всех значений X, при которых целевая функция будет минимальной. |



 (1.1)
(1.1) (1.2)
(1.2) (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) (1.10)
(1.10)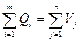
 (1.11)
(1.11) (1.12)
(1.12) (1.13)
(1.13) (1.14)
(1.14) (1.15)
(1.15) называется целевой функцией или
называется целевой функцией или