Тема 10 Оптимальная стратегия обновления оборудования
Предприятие в начале пятилетнего периода выделило 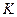 =4,5 млн. руб. для комплектования оборудования, стоимость единицы которого =4,5 млн. руб. для комплектования оборудования, стоимость единицы которого  =1,5 млн. руб. Единица оборудования за год приносит предприятию =1,5 млн. руб. Единица оборудования за год приносит предприятию  =0,6 млн. руб. прибыли. Необходимо разработать такую программу пополнения оборудования, чтобы суммарная прибыль от его внедрения в течение планового периода была максимальной. =0,6 млн. руб. прибыли. Необходимо разработать такую программу пополнения оборудования, чтобы суммарная прибыль от его внедрения в течение планового периода была максимальной. Решение. Выигрыш – прибыль от внедрения оборудования. Управление  – доля прибыли i-го года, идущая на закупку оборудования в следующем (i+1)-ом году: – доля прибыли i-го года, идущая на закупку оборудования в следующем (i+1)-ом году:  . Общее число единиц нового оборудования к концу i-го года обозначим через . Общее число единиц нового оборудования к концу i-го года обозначим через  . . I этап. Построение целевой функции F. Первый год. На выделенные средства предприятие закупает  единицы оборудования. Если число получилось нецелое, то надо его округлить до меньшего целого значения и найти остаток неистраченной суммы. Суммарная годовая прибыль от приобретенного оборудования составит единицы оборудования. Если число получилось нецелое, то надо его округлить до меньшего целого значения и найти остаток неистраченной суммы. Суммарная годовая прибыль от приобретенного оборудования составит  . Доля этой прибыли . Доля этой прибыли  пойдет на приобретение оборудования на второй год, а доля (1- пойдет на приобретение оборудования на второй год, а доля (1-  ) останется в распоряжении предприятия (если есть остаток неистраченной суммы, то его надо прибавить к первой доли, так как эти деньги предназначены для покупки оборудования). Эта прибыль будет равна: ) останется в распоряжении предприятия (если есть остаток неистраченной суммы, то его надо прибавить к первой доли, так как эти деньги предназначены для покупки оборудования). Эта прибыль будет равна:  . (1) . (1)
Второй год. На второй год новое оборудование будет приобретаться за счет части прибыли 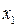 , полученной в течение первого года. Эта величина равна , полученной в течение первого года. Эта величина равна  . Используя ее, можно в течение второго года дополнительно приобрести . Используя ее, можно в течение второго года дополнительно приобрести  единиц нового оборудования. Всего к концу второго года в распоряжении предприятия будет единиц нового оборудования. Всего к концу второго года в распоряжении предприятия будет   единиц оборудования. единиц оборудования. На третий год на закупку нового оборудования используем долю  прибыли, полученной за второй год. В распоряжении предприятия за второй год остается прибыль прибыли, полученной за второй год. В распоряжении предприятия за второй год остается прибыль  . (2) . (2)
Третий год. На третий год на закупку оборудования пойдет  млн. руб. Это позволит дополнительно закупить млн. руб. Это позволит дополнительно закупить 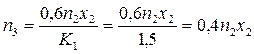 единиц оборудования. Количество оборудования к концу третьего года будет составлять единиц оборудования. Количество оборудования к концу третьего года будет составлять   единиц. единиц.
Общая прибыль от внедрения оборудования будет равна  . На приобретение нового оборудования на четвертый год пойдет сумма . На приобретение нового оборудования на четвертый год пойдет сумма  млн. руб. В распоряжении предприятия остается доля прибыли млн. руб. В распоряжении предприятия остается доля прибыли 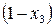 , что составит , что составит  . (3) . (3)
Четвертый год. На четвертый год на закупку оборудования пойдет  млн. руб. Это позволит закупить дополнительно млн. руб. Это позволит закупить дополнительно 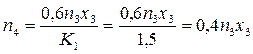 единиц. Количество оборудования к концу четвертого года будет единиц. Количество оборудования к концу четвертого года будет   единиц. Прибыль от его внедрения составит единиц. Прибыль от его внедрения составит  млн. руб. млн. руб. На приобретение нового оборудования на пятый год пойдет сумма  млн. руб. У предприятия останется прибыль млн. руб. У предприятия останется прибыль  . (4) . (4)
Пятый год. На пятый год на закупку оборудования пойдет сумма  млн. руб. Это позволит закупить дополнительно млн. руб. Это позволит закупить дополнительно 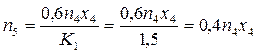 единиц. Количество оборудования к концу четвертого года будет единиц. Количество оборудования к концу четвертого года будет   единиц. единиц. Так как этот год последний в плановом периоде, то выделение средств на закупку оборудования не планируется и вся прибыль остается у предприятия: 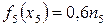 . (5) . (5)
Целевая функция данной задачи представляет собой суммарную прибыль за весь пятилетний период, которая равна сумме прибылей за каждый год: 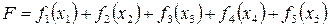
Эта функция зависит от переменных  , , 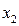 , ,  , ,  , ,  . Таким образом, задача состоит в определении таких значений переменных, при которых F достигает максимума. . Таким образом, задача состоит в определении таких значений переменных, при которых F достигает максимума. 2 этап. Решение задачи «в обратном порядке». Обозначим суммарную нарастающую прибыль, получаемую от внедрения нового оборудования через  , то есть , то есть 



 . .
Согласно принципу оптимальности Беллмана будем решать задача «в обратном порядке» - от пятого года к первому. Прибыль за все пять лет:  . (6) . (6)
Прибыль за четыре года:  . (7) . (7)
Подставляя (7) в (6), получаем:  . (8) . (8)
Из формулы (8) делаем вывод о том, что  при при  , то есть , то есть  . (9) . (9)
Прибыль за три года:  . (10) . (10)
Подставляя (10) в (9) и учитывая формулу для  , получаем: , получаем:  . (11) . (11)
Из формулы (11) делаем вывод о том, при  , то есть , то есть  . (12) . (12)
Прибыль за три года:  . (13) . (13)
Подставляя (10) в (9) и учитывая формулу для  , получаем: , получаем:  . (14) . (14)
Из формулы (14) делаем вывод о том, что  при при  , то есть , то есть  . (15) . (15)
Прибыль за два года:  . (16) . (16)
Подставляя (16) в (15) и учитывая формулу для  , получаем: , получаем:  . (17) . (17)
Из формулы (17) делаем вывод о том, что  при при  , то есть , то есть  . (18) . (18)
Прибыль за первый год и значение для  вычислены ранее: вычислены ранее:  , , 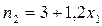 . Подставляя их в (18). Получим: . Подставляя их в (18). Получим:
 . (19) . (19)
Из формулы (19) делаем вывод о том, что  при при  , то есть , то есть  млн. руб. млн. руб.
Так как  - целевая функция задачи, то решение окончено. - целевая функция задачи, то решение окончено. Ответ: максимальная прибыль за пять лет, равная 10,584 млн. руб., будет получена в том случае, если в течение первого и второго года всю прибыль направить на закупку нового оборудования(  ), а в течение третьего, четвертого и пятого годов новое оборудование не покупать ( ), а в течение третьего, четвертого и пятого годов новое оборудование не покупать (  ). ). Контрольное задание №10
| 



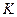 =4,5 млн. руб. для комплектования оборудования, стоимость единицы которого
=4,5 млн. руб. для комплектования оборудования, стоимость единицы которого  =1,5 млн. руб. Единица оборудования за год приносит предприятию
=1,5 млн. руб. Единица оборудования за год приносит предприятию  =0,6 млн. руб. прибыли. Необходимо разработать такую программу пополнения оборудования, чтобы суммарная прибыль от его внедрения в течение планового периода была максимальной.
=0,6 млн. руб. прибыли. Необходимо разработать такую программу пополнения оборудования, чтобы суммарная прибыль от его внедрения в течение планового периода была максимальной. – доля прибыли i-го года, идущая на закупку оборудования в следующем (i+1)-ом году:
– доля прибыли i-го года, идущая на закупку оборудования в следующем (i+1)-ом году:  . Общее число единиц нового оборудования к концу i-го года обозначим через
. Общее число единиц нового оборудования к концу i-го года обозначим через  .
. единицы оборудования. Если число получилось нецелое, то надо его округлить до меньшего целого значения и найти остаток неистраченной суммы. Суммарная годовая прибыль от приобретенного оборудования составит
единицы оборудования. Если число получилось нецелое, то надо его округлить до меньшего целого значения и найти остаток неистраченной суммы. Суммарная годовая прибыль от приобретенного оборудования составит  . Доля этой прибыли
. Доля этой прибыли  пойдет на приобретение оборудования на второй год, а доля (1-
пойдет на приобретение оборудования на второй год, а доля (1-  ) останется в распоряжении предприятия (если есть остаток неистраченной суммы, то его надо прибавить к первой доли, так как эти деньги предназначены для покупки оборудования). Эта прибыль будет равна:
) останется в распоряжении предприятия (если есть остаток неистраченной суммы, то его надо прибавить к первой доли, так как эти деньги предназначены для покупки оборудования). Эта прибыль будет равна: . (1)
. (1)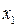 , полученной в течение первого года. Эта величина равна
, полученной в течение первого года. Эта величина равна  . Используя ее, можно в течение второго года дополнительно приобрести
. Используя ее, можно в течение второго года дополнительно приобрести  единиц нового оборудования. Всего к концу второго года в распоряжении предприятия будет
единиц нового оборудования. Всего к концу второго года в распоряжении предприятия будет 
 единиц оборудования.
единиц оборудования. прибыли, полученной за второй год. В распоряжении предприятия за второй год остается прибыль
прибыли, полученной за второй год. В распоряжении предприятия за второй год остается прибыль . (2)
. (2) млн. руб. Это позволит дополнительно закупить
млн. руб. Это позволит дополнительно закупить 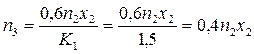 единиц оборудования. Количество оборудования к концу третьего года будет составлять
единиц оборудования. Количество оборудования к концу третьего года будет составлять
 единиц.
единиц. . На приобретение нового оборудования на четвертый год пойдет сумма
. На приобретение нового оборудования на четвертый год пойдет сумма  млн. руб. В распоряжении предприятия остается доля прибыли
млн. руб. В распоряжении предприятия остается доля прибыли 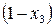 , что составит
, что составит . (3)
. (3) млн. руб. Это позволит закупить дополнительно
млн. руб. Это позволит закупить дополнительно 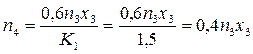 единиц. Количество оборудования к концу четвертого года будет
единиц. Количество оборудования к концу четвертого года будет 
 единиц. Прибыль от его внедрения составит
единиц. Прибыль от его внедрения составит  млн. руб.
млн. руб. млн. руб. У предприятия останется прибыль
млн. руб. У предприятия останется прибыль . (4)
. (4)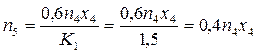 единиц. Количество оборудования к концу четвертого года будет
единиц. Количество оборудования к концу четвертого года будет 
 единиц.
единиц.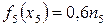 . (5)
. (5)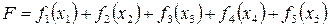
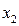 ,
,  ,
,  ,
,  . Таким образом, задача состоит в определении таких значений переменных, при которых F достигает максимума.
. Таким образом, задача состоит в определении таких значений переменных, при которых F достигает максимума. , то есть
, то есть



 .
. . (6)
. (6) . (7)
. (7) . (8)
. (8) при
при  , то есть
, то есть . (9)
. (9) . (10)
. (10) , получаем:
, получаем: . (11)
. (11) , то есть
, то есть . (12)
. (12) при
при  . (16)
. (16) , получаем:
, получаем: . (17)
. (17) , то есть
, то есть . (18)
. (18) вычислены ранее:
вычислены ранее: ,
, 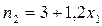 . Подставляя их в (18). Получим:
. Подставляя их в (18). Получим: . (19)
. (19) , то есть
, то есть млн. руб.
млн. руб. - целевая функция задачи, то решение окончено.
- целевая функция задачи, то решение окончено. ), а в течение третьего, четвертого и пятого годов новое оборудование не покупать (
), а в течение третьего, четвертого и пятого годов новое оборудование не покупать (  ).
).