 ПОЗНАВАТЕЛЬНОЕ
| Решение матричной игры в смешанных стратегиях
Игра, заданная некоторой матрицей, может не иметь седловой точки. Пример 3Рассмотрим платёжную матрицу
Для первого игрока находим максимин
Для второго игрока находим минимакс
Следовательно, минимакс и максимин не совпадают, т.е. положения равновесия в чистых стратегиях не существует. Если среди чистых стратегий решения игры нет, то для его нахождения используются смешанные стратегии. Справедлива теорема. Теорема Неймана(основная теорема теории игр)Каждая конечная игра имеет,по крайней мере, одно оптимальное решение, возможно среди смешанных стратегий. При этом если
является ценой игры. Определение.Если чистая стратегия входит в смешанную с ненулевой вероятностью, то она называется активной Активные стратегии обладают свойством, выражаемым следующей теоремой. Теорема(об активных стратегиях) Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остаётся неизменным и равным цене игры Игра с природой
Кроме антогонистических рассматривают так называемые неантогонистические игры. В этом случае предполагают, что действия противника не носят характер строгого противостояния. Его интересы могут быть разными и в общем случае не совпадающими с нашими, однако они не являются «злонамеренно» направленными против нас. Простейшим примером такой ситуации является следующая. Предположим, что известна (в общем случае смешанная) стратегия применяемая одним из игроков. Например, из опыта предыдущих наблюдений. Этот игрок использует свою стратегию вне зависимости от нашей стратегии. Такую игру принято называть игрой с природой. Природа как бы не имея в общем желания нам навредить действует по своим законам. Пусть торговое предприятие имеет т стратегий: По платежной матрице можно принять ряд решений. Например, оценить возможные исходы: минимальный выигрыш
т.е. наименьшая из величин в каждой
При анализе «игры с природой» вводится показатель, по которому оценивают, насколько то или иное состояние «природы» влияет на исход ситуации. Этот показатель называют риском. Риск
Исходя из этого определения можно оценить максимальный риск каждого решения:
Решения могут приниматься по результатам анализа ряда критериев.
|





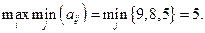
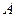 - платежная матрица,
- платежная матрица,  - оптимальная смешанная стратегия первого игрока, a
- оптимальная смешанная стратегия первого игрока, a  - второго, то число
- второго, то число
 , если второй игрок не выходит за пределы своих активных стратегий.
, если второй игрок не выходит за пределы своих активных стратегий. и имеется n возможных состояний природы:
и имеется n возможных состояний природы:  . Так как природа не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить выигрышем
. Так как природа не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить выигрышем  первой стороны для каждой пары стратегий
первой стороны для каждой пары стратегий  и
и  . Все показатели игры заданы платежной матрицей
. Все показатели игры заданы платежной матрицей  размерности
размерности 

 -й строке как пессимистическая оценка; максимальный выигрыш – то наилучшее, что дает выбор
-й строке как пессимистическая оценка; максимальный выигрыш – то наилучшее, что дает выбор 
 при пользовании стратегией
при пользовании стратегией  и выигрышем
и выигрышем 
