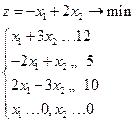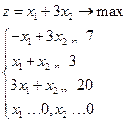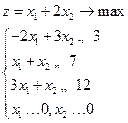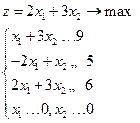ПОЗНАВАТЕЛЬНОЕ
| Не единственность оптимального решения
Рассмотрим задачу:
Геометрическое решение задачи показано на рисунке 3. Из него следует, что линия уровня с максимальным уровнем совпадает с граничной линией АВ области допустимых решений ABCD, т.е. с линией Замечание.Данная ситуация возможна только в том случае, если коэффициенты целевой функции пропорциональны коэффициентам какой-либо прямой ограничений. Это условие является только необходимым, но не является достаточным. Следовательно, на всем отрезке АВ целевая функция z принимает одно и то же оптимальное значение. Это означает, что задача имеет бесконечное множество оптимальных решений (их задают координаты отрезка АВ), среди которых базисных оптимальных решений два –соответственно в угловых точках
Максимальное значение целевой функции можно найти, подставив координаты любой точки отрезка АВ в уравнение целевой функции. В рассматриваемом случае
Рис. 3 Пример.Решить задачу линейного программирования симплекс-методом:
Решение.Приведем систему ограничений к каноническому виду. Получим расширенную систему:
Целевую функцию представим в виде Заполняем первую симплекс-таблицу:
Проверяем критерий оптимальности задачи. В последней оценочной строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю - (-3). Следовательно, Находим оценочные отношения и выбираем из них минимальное (5). Следовательно, а) в новом базисе основные переменные б) расставляем 0 и 1; например, на пересечении столбца и строки, соответствующих переменной Получаем вторую симплекс-таблицу:
Критерий оптимальности вновь не выполнен. Теперь разрешающий первый столбец и Переходим к новой симплекс-таблице:
и на этот раз критерий оптимальности не выполнен. Выводимая переменная
Критерий оптимальности выполнен. Следовательно, Контрольное задание №2. Решить графически и симплекс-методом задачу линейного программирования:
|





 и
и  (точки находятся как решения соответствующих уравнений). Точки отрезка АВ задаются как линейная комбинация точек А и В:
(точки находятся как решения соответствующих уравнений). Точки отрезка АВ задаются как линейная комбинация точек А и В:
 .
.


 Базисными переменными будут являться дополнительные переменные
Базисными переменными будут являться дополнительные переменные  .
.




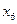


 . Переменная
. Переменная 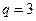 , переменная
, переменная  ;
; . Остальные клетки таблицы заполняем по формулам (2). Например:
. Остальные клетки таблицы заполняем по формулам (2). Например: 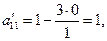

 .
. Оптимальное решение
Оптимальное решение