 ПОЗНАВАТЕЛЬНОЕ
| Многоотраслевой экономики (балансовая модель)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Малаховский Н.В. Методические указания и контрольные задания Для студентов заочного отделения По дисциплине экономико-математические методы
Калининград 2014
Оглавление
Тема 1 Модель Василия Леонтьева многоотраслевой экономики........….……………..3 Контрольное задание №1……………………………………………………………………..5 Тема 2. Линейное программирование………………………………………………………6 Контрольное задание №2……………………………………………………………………..11 Тема 3. Двойственные задачи линейного программирования……...…………….....…12 Контрольное задание №3……………………………………………………………………..14 Тема 4. Динамическое программирование………………………………………………..15 Контрольное задание №4……………………………………………………………………..18 Тема 5. Элементы теории игр .…………………………………………………..…………..22 Контрольное задание №5……………………………………………………………………..31 Тема 6. Сетевые модели планирования и управления………………………………….33 Контрольное задание №6……………………………………………………………………..39 Тема 7. Задача об оптимальном назначении ……………………………………………...45 Контрольное задание №7……………………………………………………………………..47 Тема 8. Модель экономичного заказа (управление товарными запасами)....................49 Контрольное задание №8…………………………………………………………………….50 Тема 9. Моделирование систем массового обслуживания (СМО)...................................50 Контрольное задание №9……………………………………………………………………..54 Тема 10. Оптимальная стратегия обновления оборудования……..................................57 Контрольное задание №10……………………………………………………………..…….60 Тема 11 Транспортная задача линейного программирования………………………107 Контрольной задание №11………………………………………………………………..126 Правила выполнения контрольной работы В соответствии с учебным планом студенты выполняют индивидуальное задание по курсу экономико-математические методы и сдают зачет. Индивидуальное задание необходимо выполнять в тетради синими чернилами, оставляя поля для замечаний преподавателя. На обложке тетради должны быть четко написаны фамилия, имя, отчество студента, название дисциплины и группы. Индивидуальное задание должно содержать решение всех задач, указанных в задании, строго по своему варианту. Индивидуальное задание, содержащее решение не всех задач, а так же решение задач не своего варианта, не засчитываются. Решения задач следует располагать в порядке номеров, указанных в заданиях, сохраняя номера задач. Перед решением каждой задачи необходимо написать полностью ее условие. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения. Индивидуальное задание состоит из 10 задач. Каждая задача содержит 20 вариантов. Номер варианта индивидуального задания выбирается по номеру студента в журнале.
Тема 1. Модель Василия Леонтьева многоотраслевой экономики (балансовая модель)
Модель многоотраслевой экономики была разработана в 1936 году американским экономистом Василием Леонтьевым. Модель Леонтьева применяется в макроэкономике и связана с ведением многоотраслевого хозяйства. Целью построения данной модели является выяснение объема производства каждой из Предположим, что рассматривается Рассмотрим период в 1 год. Введем обозначения:
Так как валовой объем продукции
которое называется соотношением баланса. Будем рассматривать модель в стоимостном выражении. Введем коэффициенты прямых затрат:
Коэффициент прямых затрат показывает затраты
В этом случае соотношение баланса примет вид:
В соответствии с экономическим смыслом задачи
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска Х, который, при известной матрице прямых затрат А, обеспечивает заданный вектор конечного продукта. Перепишем уравнение в виде: Матрица Критерий продуктивности матрицы Задача.В таблице приведены данные об использовании баланса за отчетный период (в условных денежных единицах):
Вычислить необходимый объем валового выпуска каждой отрасли, если конечное потребление энергетической отрасли увеличится вдвое, а машиностроения сохранится на прежнем уровне. Решение. Имеем
Находим коэффициенты прямых затрат: Матрица прямых затрат Следовательно, для любого вектора Найдем матрицу полных затрат По условию вектор конечного продукта Контрольное задание №1
В таблице приведены данные об использовании баланса за отчетный период (в условных денежных единицах):
Вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличится на 10%, второй отрасли - на 20%, а третьей отрасли- на 30% (КП- конечный продукт).
|



 отраслей производства, который бы удовлетворял все потребности в продукции этой отрасли. При этом каждая отрасль выступает как производитель продукции и как потребитель продукции, произведенной в этой и в других отраслях производства.
отраслей производства, который бы удовлетворял все потребности в продукции этой отрасли. При этом каждая отрасль выступает как производитель продукции и как потребитель продукции, произведенной в этой и в других отраслях производства. - общий (валовой объем)
- общий (валовой объем)  -ой отрасли производства,
-ой отрасли производства, 
 - объем продукции, произведенной
- объем продукции, произведенной  - ой отраслью;
- ой отраслью; - объем конечного продукта
- объем конечного продукта 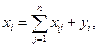




 при
при  и
и  . Обозначим:
. Обозначим: - вектор валового выпуска;
- вектор валового выпуска;  - вектор конечного продукта;
- вектор конечного продукта;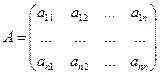 - матрица прямых затрат. Тогда систему соотношений баланса можно записать в матричном виде:
- матрица прямых затрат. Тогда систему соотношений баланса можно записать в матричном виде: 
 Если матрица
Если матрица  не вырождена т.е.
не вырождена т.е.  то
то  Матрица
Матрица  называется матрицей полных затрат. Каждый элемент матрицы
называется матрицей полных затрат. Каждый элемент матрицы  показывает величину валового выпуска продукции
показывает величину валового выпуска продукции 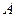 называется продуктивной, если для любого
называется продуктивной, если для любого  существует решение
существует решение  матричного уравнения. В этом случае и модель Леонтьева называется продуктивной.
матричного уравнения. В этом случае и модель Леонтьева называется продуктивной.
 матрицы
матрицы  и существует столбец
и существует столбец  такой, что
такой, что 



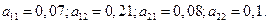
 имеет неотрицательные элементы и удовлетворяет критерию продуктивности:
имеет неотрицательные элементы и удовлетворяет критерию продуктивности: 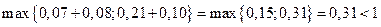 .
.

 тогда получаем вектор валового выпуска
тогда получаем вектор валового выпуска  .
.