 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Свойства политропных процессов
Перечислим важные свойства, которыми обладают политропные процессы. Если в политропном процессе к идеальному газу подводится или отводится тепловая энергия
Покажем это. Введем обозначения
Из первого закона термодинамики следует, что
Покажем, что для политропных процессов
Отсюда и из равенства (9.15) следует, что Следующим важным свойством обратимых политропных процессов в идеальном газе является возможность представлять в аналитическом виде изменение энтропии в процессе, через независимые начальные и текущие параметры процесса. Покажем это. Известно, что для обратимых процессов изменение энтропии определяется равенством
С учетом соотношения (9.1) это равенство запишем в виде
После интегрирования обеих частей последнего уравнения получим:
С учетом выражения (9.9)
Если учесть следующие соотношения, справедливые для политроп-ных процессов:
то выражение для изменения энтропии примет вид:
Из равенства (9.17) с помощью потенцирования можно получить следующую связь между изменением абсолютной температуры и изменением энтропии в политропном процессе:
Это равенство используется для построения графиков политропных процессов в Т—s координатах. Анализ частных случаев Изохорный процесс Задача 9.1. Доказать, что для этого случая из уравнения политропы Покажем, что в этом случае обмен тепловой энергией q между газом и внешней средой происходит только за счёт изменения внутренней энергии газа Действительно, для изохорного процесса

Рис. 9.1. К изохорному процессу
Изохорные процессы используют, например, в карбюраторных двигателях внутреннего сгорания для увеличения внутренней энергии рабочего тела (продуктов сгорания топлива в воздухе) путем сжигания горючего в кислороде воздуха. Здесь вся тепловая энергия, выделившаяся при сгорании топлива, идет только на увеличение внутренней энергии рабочего тела. Отметим, что в p—V координатах линия Изменение энтропии в изохорном процессе определяется равенством
Связь температуры с энтропией в изохорном процессехарактеризуется соотношением (см. рис. 9.1):
Изобарный процесс ( Из уравнения политропы Покажем, что в изобарном процессе обмен тепловой энергией между газом и внешней средой происходит за счет изменения энтальпии газа Действительно, для изобарного процесса
Рис. 9.2. К изобарному процессу
Изобарный процесс применяют в дизелях иреактивных двигателях для организации горения топлива в камерах сгорания. Здесь вся тепловая энергии, выделившаяся при сгорании топлива, идет на увеличение энтальпии рабочего тела, которое в реактивных двигателях используется для разгона продуктов сгорания с помощью специально спрофилированного канала-сопла. Для изобарного процесса первый закон термодинамики может быть записан также в форме для внутренней энергии Так как
то
Пример 9.1. Для воздуха k=1,4, поэтому в изобарном процессе для воздуха Пример 9.2. Все процессы кондиционирования атмосферного воздуха, связанные с его нагревом и охлаждением, увлажнением и осушкой, проходят при изобарных процессах, так как давление воздуха при указанной его обработке остается постоянным и равным давлению атмосферы. Изменение энтропии в изобарном процессе определяется равенством:
Связь температуры с энтропией в этом процессе характеризуется соотношением (рис. 9.2):
Замечание 9.1. Так как для большинства тел, в том числе и для идеального газа, ср>
Рис. 9.3. Изохора и изобара в T–s координатах
|



 , то относительная доля тепловой энергии
, то относительная доля тепловой энергии  , которая идет на изменение внутренней энергии тела, а также относительная доля тепловой энергии
, которая идет на изменение внутренней энергии тела, а также относительная доля тепловой энергии  , которая идет на совершение телом работы l против внешней среды, являются величинами постоянными в течение всего процесса, т. е.
, которая идет на совершение телом работы l против внешней среды, являются величинами постоянными в течение всего процесса, т. е.

 (9.15)
(9.15) , тогда из (9.15) следует, что и
, тогда из (9.15) следует, что и 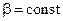 . Действительно, для политропных процессов в идеальном газе справедливы равенства.
. Действительно, для политропных процессов в идеальном газе справедливы равенства.
 . Таким образом, утверждения, изложенные выше, доказаны.
. Таким образом, утверждения, изложенные выше, доказаны.
 или
или  (9.16)
(9.16)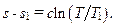 (9.17)
(9.17) (9.18)
(9.18) (9.19)
(9.19) (9.20)
(9.20)  (9.21)
(9.21) (9.22)
(9.22) . Для изохорного процесса
. Для изохорного процесса  Из равенства
Из равенства  следует, что
следует, что 
 следует, что
следует, что  ; вся подведенная тепловая энергия идет только на увеличение внутренней энергии тела.
; вся подведенная тепловая энергия идет только на увеличение внутренней энергии тела. , поэтому
, поэтому  , ивыражение дляпервого закона термодинамики
, ивыражение дляпервого закона термодинамики 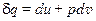 примет вид
примет вид  Отсюда следует, что
Отсюда следует, что  , т. е. обмен тепловой энергией между газом и внешней средой происходит только за счет изменения внутренней энергии газа
, т. е. обмен тепловой энергией между газом и внешней средой происходит только за счет изменения внутренней энергии газа  >0, и область, где
>0, и область, где 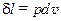 совпадает со знаком изменения объема
совпадает со знаком изменения объема 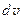 .
. (9.23)
(9.23) (9.24)
(9.24) )Дляэтого процесса
)Дляэтого процесса  Из равенства
Из равенства  следует, что
следует, что  .
. следует, что
следует, что  .
. , и первый закон термодинамики, записанный в форме для энтальпии
, и первый закон термодинамики, записанный в форме для энтальпии  , примет вид
, примет вид  , что и требовалось показать.
, что и требовалось показать.
 . Отсюда можно определить, какая относительная доля тепловой энергии идет на изменение внутренней энергии, а какая — на совершение работы газом против внешних сил, т. е. определить величины
. Отсюда можно определить, какая относительная доля тепловой энергии идет на изменение внутренней энергии, а какая — на совершение работы газом против внешних сил, т. е. определить величины  и
и  .
.

 , следовательно, здесь 2/3 тепловой энергии идет на изменение внутренней энергии, а 1/3 на работу против внешних сил давления, например, против сил атмосферного давления.
, следовательно, здесь 2/3 тепловой энергии идет на изменение внутренней энергии, а 1/3 на работу против внешних сил давления, например, против сил атмосферного давления. (9.25)
(9.25)
 , то в системе координат T—s линия изохоры
, то в системе координат T—s линия изохоры  проходит круче изобары
проходит круче изобары  , если эти линии проходят через одну точку (рис. 9.3). Исключение составляет вода в диапазоне температур от 0 оС до 4 оС, здесь ср>
, если эти линии проходят через одну точку (рис. 9.3). Исключение составляет вода в диапазоне температур от 0 оС до 4 оС, здесь ср>  , и ряд других тел.
, и ряд других тел.