 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Применение первого закона термодинамики для анализа политропных процессов
Прежде чем получить частное решение уравнений термодинамики для политропных процессов в идеальных газах, рассмотрим возможность получения общего решения уравнений термодинамики для таких газов, которые определяются уравнениями, описывающими модель идеального газа и термодинамического процесса. Модель идеального газа определяется соотношениями
Любые термодинамические процессы описываются первым законом термодинамики
Таким образом, общая модель термодинамических процессов в идеальном газе представляет собой систему дифференциальных и алгебраических уравнений (9.2) и (9.3). Выясним условия, при которых эта система имеет решение. Запишем первый закон термодинамики в двух формах для внутренней энергии
Из определения теплоемкости следует, что
Используя это соотношение, запишем равенства ( 9.4 ) в виде
Известно, что для идеального газа
С учетом этих зависимостей соотношения (9.6) примут вид:
Разделив первое равенство на второе, получим
или
Легко видеть, что для того, чтобы получить общее решение дифференциального уравнения (9.7), необходимо знать зависимость Однако решение этого уравнения можно получить для различных частных случаев, например, при условии, что теплоемкость рабочего тела остается постоянной Введем обозначение
Здесь n называется показателем политропного процесса или показателем политропы. Из (9.8) следует, что
С учетом обозначения (9.8) дифференциальное уравнение,описывающее любой политропный процесс, примет вид
После интегрирования обеих частей этого уравнения получим
или
После интегрирования обеих частей последовательного равенства получим окончательно
Это выражение является простейшим частным решением системы алгебраических и дифференциальных уравнений (9.2), (9.3) при условии, что Таким образом, политропные процессы — это такие процессы, для которых система дифференциальных и алгебраических уравнений (9.2), (9.3), описывающая модель обратимых термодинамических процессов в идеальном газе, имеет решение в аналитическом виде (9.11). По устоявшейся традиции это решение называют уравнением политропы или уравнением состояния политропного процесса. Из него следует, что для любых двух и более состояний рабочего тела, участвующего в данном политропном процессе, имеют место равенства
В курсе физики уже получали подобную связь давления с объемом для адиабатного процесса в виде
Соотношения (9.13) могут быть получены из (9.12) заменой n на k. Это понятно, т. к. адиабатный процесс является частным случаем политропных процессов при n=k. Поэтому по аналогии с адиабатным процессом в любом политропном процессе для удельной работы расширения
при условии, что Можно показать, что для политропных процессов справедливо равенство:
В самом деле, из уравнения политропы следует:
или
Из последнего равенства получим
Используя последнее соотношение, удельную работу расширения l в политропном процессе запишем в виде
|



 (9.2)
(9.2) (9.3)
(9.3)
 и для энтальпии
и для энтальпии  :
: (9.4)
(9.4) (9.5)
(9.5) (9.6)
(9.6)


 (9.7)
(9.7) .В общем случае такую зависимость для любых процессов идеального газа получить нельзя. Поэтому нельзя получить решение уравнения (9.7) в общем случае даже для идеальных газов.
.В общем случае такую зависимость для любых процессов идеального газа получить нельзя. Поэтому нельзя получить решение уравнения (9.7) в общем случае даже для идеальных газов.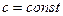 в течение всего процесса, т. е. для политропных процессов. В этом случае дифференциальное уравнение (9.7) можно решить методом разделения переменных.
в течение всего процесса, т. е. для политропных процессов. В этом случае дифференциальное уравнение (9.7) можно решить методом разделения переменных. (9.8)
(9.8) (9.9)
(9.9) (9.10)
(9.10)

 (9.11)
(9.11) (9.12)
(9.12) (9.13)
(9.13)
 , имеем
, имеем 
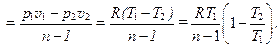



 или
или  (9.14)
(9.14)