 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Понятие о равновесных и неравновесных процессах.
Лекция 8. Термодинамические процессы. Вторая важная гипотеза состоит в том, что если состояние системы изменяется, то изменение происходит бесконечно медленно, так что этот процесс можно представить в виде непрерывной последовательности равновесных состояний.
Рис. 2.3. К понятию о равновесном процессе
Пример 2.5. Процесс сжатия газа поршнем с помощью песчинок, которые насыпаются на его поверхность бесконечно медленно, при условии, что масса каждой песчинки стремится к нулю, а их число — к бесконечности, будет равновесным процессом (рис. 2.3). Если равновесный процесс — это бесконечно медленный процесс, то неравновесный процесс — это любой процесс, протекающий с конечной скоростью. Пример 2.6. Процесс сжатия или расширения газа с конечной скоростью W с помощью поршня в цилиндре является неравновесным процессом. Равновесные процессы как процессы последовательного прохождения системой ряда равновесных состояний изображаются кривыми линиями в некоторых системах координат. Например, процесс бесконечно медленного сжатия газа поршнем в цилиндре можно изобразить в системе координат p-V кривой 1-2 (рис. 2.4).
0 v Рис. 2.4. Изображение равновесного процесса
Неравновесный процесс нельзя изобразить с помощью некоторой линии в любой системе координат (рис. 2.5). Равновесное состояние достигается при равенстве параметров рабочего тела и внешней среды. Так, для рассмотренного примера равновесие достигается при равенстве давлений, которые оказывают на поршень газ и внешняя среда.
p ? 0 v Рис. 2.5. К понятию о неравновесном процессе
Вообще, если среди нетепловых воздействий на систему рассматривать только механическое, то механическое равновесие системы достигается при равенстве давлений внутри рабочего тела и внешней среды. Тепловое же равновесие возможно только при равенстве температур тела и внешней среды. Отсюда следует, что равновесный процесс — это бесконечно медленный процесс изменения состояния системы, когда параметры системы и среды получают одинаковые бесконечно малые приращения. Кроме того, равновесный процесс можно рассматривать как предельный случай неравновесного процесса, когда разность давлений и температур между системой и окружающей средой стремится к нулю. Итак, гипотезы о равновесном состоянии и равновесных процессах изменения термодинамического состояния системы, позволяют рассматривать систему как единое целое. Это очень важно, так как в этом случае существенно снижается число параметров, описывающих состояние системы. Пример 2.7. Состояние идеального газа вполне определяется заданием всего только двух параметров, например, давления р и объема V. Остальные параметры зависят от этих двух параметров, например, S = S (р, V), здесь S — энтропия. Кроме того, описанный выше термодинамический подход, основанный на предположении о равновесности рассматриваемых процессов, позволяет считать параметры системы не зависящими ни от времени, ни от координат точек системы (см. пример 2.3). Это существенно упрощает решение задач термодинамики, которые в равновесных процессах сводятся к системе алгебраических и дифференциальных соотношений относительно неизвестных параметров. Зачастую эту систему удается решить в аналитическом виде (например, для политропных процессов). Неравновесные же процессы довольно сложны. Здесь уже необходимо учитывать время процесса, которое для неравновесных процессов является конечным. Кроме того, если, в равновесном процессе все термодинамические соотношения записываются и решаются для всей системы в целом, то в неравновесном процессе это делается для каждой точки системы отдельно. Поэтому, кроме времени, учитываются еще и координаты точек системы, и все параметры зависят как от времени t, так и от вектора координат точек системы Реальные неравновесные процессы являются результатом воздействия на систему извне, которое выводит ее из состояния термодинамического равновесия. Поэтому все реальные процессы являются неравновесными. В термодинамике реальные неравновесные процессы всегда для простоты заменяют равновесными (неравновесные процессы исследуются в неравновесной термодинамике). В качестве параметров равновесных процессов принимают осредненные параметры, соответствующие каждому состоянию системы в неравновесном процессе. Это всегда оправдывается в случаях, когда время изменения параметров системы в рассматриваемом процессе достаточно велико по сравнению со временем релаксации системы. Временем релаксации системы называется максимальное время, в течение которого система, выведенная из состояния равновесия, приходит в равновесное состояние. Для газа, время релаксации τр определяется характерным размером сосуда L, в котором он находится, и скоростью звука a, с которой малые («слабые») возмущения параметров («сильные» возмущения формируются на фронте ударной волны, которая движется со скоростью большей, чем скорость звука) распространяются по объему газа и выравнивают значения всех параметров в сосуде:
Пример 2.8. Скорость распространения «слабых» возмущений (изменений) параметров в газе приближенно равна 300 м/с. Если длина рабочей части цилиндра двигателя внутреннего сгорания равна 0,2 м, то время релаксации для газа в таком цилиндре равно В этом примере скорость распространения волн давления, приводящих газ в равновесное состояние, значительно больше скорости движения поршня, поэтому при любом положении поршня состояние газа мало отличается от равновесного. |
Такой процесс изменения состояния системы называется равновесным. В этом процессе изменение параметров системы также происходит непрерывно и бесконечно медленно, причем изменение одноименных параметров происходит одинаково во всех точках системы, т. е. как для единого целого.
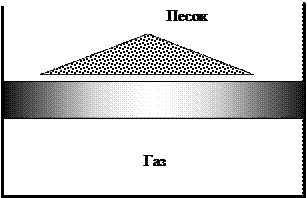
p
. Например, энтропия записывается уже так: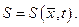 
Решение задач неравновесной термодинамики сводится к решению системы алгебраических уравнений и уравнений в частных производных, которые достаточно сложны и не всегда решаются не только аналитически, но и численно.
Если скорость движения поршня в цилиндре около 30 м/с, то процесс сжатия или расширения газа в цилиндре можно считать равновесным, так как время процесса сжатия или расширения газа равно 
т. е. на порядок больше времени релаксации tр.