Топологічні простори та топологічні многовиди. Приклади.
Нехай  - не порожня множина довільної природи, - не порожня множина довільної природи,  – множина всіх її підмножин. Множину – множина всіх її підмножин. Множину  називають топологією на називають топологією на  , якщо вона задовольняє наступним аксіомам: , якщо вона задовольняє наступним аксіомам: 1. Якщо   для всіх для всіх   де де  – множина індексів, можливо нескінченна), то – множина індексів, можливо нескінченна), то  ; порожня множина ; порожня множина   . . 2. Якщо   , , 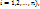 то то 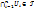 ; сама множина ; сама множина  . . Означення 1: Топологічним простором назвемо множину  , на якій визначено топологію, тобто пару , на якій визначено топологію, тобто пару  . Елементи з . Елементи з  назвемо відкритими множинами. назвемо відкритими множинами. Приклад1: Нехай  . легко бачити, що . легко бачити, що  та та  - топологічні простори з топологіями - топологічні простори з топологіями  , ,  відповідно. відповідно. На будь-якій непорожній множині можна ввести топологію, причому різними способами. Нехай 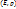 - метричний простір з метрикою (відстанню) - метричний простір з метрикою (відстанню)  , ,  - відкрита куля з центром в точці - відкрита куля з центром в точці  радіуса r>0. радіуса r>0. Множину  називають відкритою, якщо називають відкритою, якщо  . Позначимо через . Позначимо через  множину всіх відкритих в множину всіх відкритих в  множин. множин. Як відомо, побудована множина  задовольняє аксіоми 1, 2, тобто утворює топологію на задовольняє аксіоми 1, 2, тобто утворює топологію на  . Отже, будь-який метричний простір є топологічним з топологією . Отже, будь-який метричний простір є топологічним з топологією  , про яку говорять, що вона індукована метрикою , про яку говорять, що вона індукована метрикою  . . Але на будь-якій множині  можна задати метрику можна задати метрику  , наприклад покласти , наприклад покласти  , де , де  . Таким чином на кожній непорожній множині можна задати метрику, яка, в свою чергу, індукує топологію, перетворюючи цю множину в топологічний простір. . Таким чином на кожній непорожній множині можна задати метрику, яка, в свою чергу, індукує топологію, перетворюючи цю множину в топологічний простір. Означення 2: Нехай  - топологічний простір та - топологічний простір та  . Множину В називають околом множини А, якщо . Множину В називають околом множини А, якщо 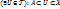 . Якщо . Якщо  , то В – окіл точки , то В – окіл точки  . . Окіл множини чи окіл точки необов’язково множина відкрита. Означення 3: Сімейство  називають базою топології називають базою топології  , якщо для кожної її точки , якщо для кожної її точки  та довільного її околу та довільного її околу   . . Вважають, що простір  є простором із зчисленною базою, якщо топологія є простором із зчисленною базою, якщо топологія  має хоч одну базу, що складається не більше ніж зі зчисленної кількості елементів. має хоч одну базу, що складається не більше ніж зі зчисленної кількості елементів. Приклад2: множина інтервалів утворює базу топології на множині дійсних чисел. Множина всіх інтервалів з раціональними кінцями утворює зчисленну базу цієї топології. Теорема 1: Нехай  – топологічний простір, – топологічний простір,  . Множина . Множина  є околом кожної своєї точки тоді і тільки тоді, коли вона відкрита. є околом кожної своєї точки тоді і тільки тоді, коли вона відкрита. Доведення: Нехай  . Для . Для  маємо: маємо:  , отже , отже  - окіл точки - окіл точки  . . Навпаки, нехай А –окіл кожної своєї точки. Тоді  : :  . . Позначимо  . Зрозуміло, що . Зрозуміло, що  . Але . Але 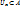 , ,  отже А отже А  . Таким чином . Таким чином  , ,  . . Означення 4: Нехай  і і  - топологічні простори. Відображення - топологічні простори. Відображення  називають неперервними в точці називають неперервними в точці  , якщо для довільного околу , якщо для довільного околу  точки точки  в в  існує окіл існує окіл  точки точки  в в  , такий, що , такий, що  . . Відображення  називають топологічним (гомеоморфізмом), якщо: називають топологічним (гомеоморфізмом), якщо: 1.  - бієкція; - бієкція; 2.  і і  неперервні на неперервні на  та та  відповідно. відповідно. Теорема 2: відображення  неперервне на неперервне на  тоді і тільки тоді, коли прообраз довільної відкритої множини з тоді і тільки тоді, коли прообраз довільної відкритої множини з  є відкрита множина в є відкрита множина в  . . Доведення: Нехай  , ,  . Нехай . Нехай  - довільна точка з - довільна точка з  і і  - довільний окіл точки - довільний окіл точки  в в  . Зa означенням 2 ( . Зa означенням 2 (  )( )(  ). Тоді ). Тоді  . Але . Але  , тобто , тобто  - окіл точки - окіл точки  . Отже, відображення . Отже, відображення  неперервне в точці неперервне в точці  Навпаки, нехай  неперервне на неперервне на  . Візьмемо довільне . Візьмемо довільне 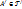 , і нехай , і нехай  - довільна точка з - довільна точка з  . Оскільки . Оскільки  неперервне в неперервне в  та та  - окіл точки - окіл точки  , то , то  - окіл точки - окіл точки  . Отже, множина . Отже, множина  є околом будь-якої своєї точки. За теоремою 1 є околом будь-якої своєї точки. За теоремою 1  , що й потрібно було встановити. , що й потрібно було встановити. Теорема 3: Нехай відображення  є гомеоморфізмом. Тоді є гомеоморфізмом. Тоді  , тобто гомеоморфізм , тобто гомеоморфізм  переводить топологію на переводить топологію на  в топологію на в топологію на  . . Доведення: За означенням 4 відображення  неперервне на неперервне на  , а відображення , а відображення  неперервне на неперервне на  . Тоді за теоремою 2 . Тоді за теоремою 2  і і  , звідки , звідки  і і  . Отже, . Отже,  . . Теорема 3 дає можливість задавати топологію на множинах, що гомеоморфні множині, на якій топологія вже відома.
Означення 5: Нехай  - відокремлюваний топологічний простір, - відокремлюваний топологічний простір,  – вимірною картою називають гомеоморфізм – вимірною картою називають гомеоморфізм  відкритої підмножини відкритої підмножини  на на  (або на його відкриту підмножину). При цьому множину (або на його відкриту підмножину). При цьому множину  називають координатним околом карти називають координатним околом карти  . . Означення 6:  – вимірним топологічним многовидом називають зв’язним, відокремлюваний топологічний простір із зчисленною базою, який можна покрити координатними околами – вимірним топологічним многовидом називають зв’язним, відокремлюваний топологічний простір із зчисленною базою, який можна покрити координатними околами  – вимірних карт. – вимірних карт. Можна довести, що гомеоморфізм переводить топологічний многовиди в топологічний многовиди тієї ж розмірності. Приклад3: Простір  зв’язний, відокремлюваний. Зчисленну базу у ньому утворює сімейство всіх можливих добутків зв’язний, відокремлюваний. Зчисленну базу у ньому утворює сімейство всіх можливих добутків  інтервалів інтервалів  з раціональними кінцями. За карту з раціональними кінцями. За карту  візьмемо тотожне перетворення візьмемо тотожне перетворення  (координатним околом цієї карти є (координатним околом цієї карти є  ). Отже ). Отже  - топологічний многовид. Застосовуючи топологічне відображення, легко показати, що афінний простір - топологічний многовид. Застосовуючи топологічне відображення, легко показати, що афінний простір  та евклідів простір та евклідів простір  також також  - вимірні топологічні многовиди. - вимірні топологічні многовиди.
| 



 - не порожня множина довільної природи,
- не порожня множина довільної природи,  – множина всіх її підмножин. Множину
– множина всіх її підмножин. Множину  називають топологією на
називають топологією на 
 для всіх
для всіх 
 де
де  – множина індексів, можливо нескінченна), то
– множина індексів, можливо нескінченна), то  ; порожня множина
; порожня множина 

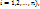 то
то 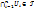 ; сама множина
; сама множина  .
. , на якій визначено топологію, тобто пару
, на якій визначено топологію, тобто пару  . Елементи з
. Елементи з  . легко бачити, що
. легко бачити, що  та
та  - топологічні простори з топологіями
- топологічні простори з топологіями  ,
,  відповідно.
відповідно.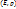 - метричний простір з метрикою (відстанню)
- метричний простір з метрикою (відстанню)  ,
,  - відкрита куля з центром в точці
- відкрита куля з центром в точці  радіуса r>0.
радіуса r>0. називають відкритою, якщо
називають відкритою, якщо  . Позначимо через
. Позначимо через  множину всіх відкритих в
множину всіх відкритих в  множин.
множин. . Отже, будь-який метричний простір є топологічним з топологією
. Отже, будь-який метричний простір є топологічним з топологією  , де
, де  . Таким чином на кожній непорожній множині можна задати метрику, яка, в свою чергу, індукує топологію, перетворюючи цю множину в топологічний простір.
. Таким чином на кожній непорожній множині можна задати метрику, яка, в свою чергу, індукує топологію, перетворюючи цю множину в топологічний простір. . Множину В називають околом множини А, якщо
. Множину В називають околом множини А, якщо 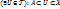 . Якщо
. Якщо  , то В – окіл точки
, то В – окіл точки  .
. називають базою топології
називають базою топології 
 .
. має хоч одну базу, що складається не більше ніж зі зчисленної кількості елементів.
має хоч одну базу, що складається не більше ніж зі зчисленної кількості елементів. . Множина
. Множина  є околом кожної своєї точки тоді і тільки тоді, коли вона відкрита.
є околом кожної своєї точки тоді і тільки тоді, коли вона відкрита. . Для
. Для  маємо:
маємо:  , отже
, отже  - окіл точки
- окіл точки  .
. :
:  .
. . Зрозуміло, що
. Зрозуміло, що  . Але
. Але 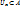 ,
,  . Таким чином
. Таким чином  ,
,  .
. - топологічні простори. Відображення
- топологічні простори. Відображення  називають неперервними в точці
називають неперервними в точці  точки
точки  в
в  існує окіл
існує окіл  точки
точки  .
. називають топологічним (гомеоморфізмом), якщо:
називають топологічним (гомеоморфізмом), якщо: неперервні на
неперервні на  тоді і тільки тоді, коли прообраз довільної відкритої множини з
тоді і тільки тоді, коли прообраз довільної відкритої множини з  ,
,  . Нехай
. Нехай  - довільний окіл точки
- довільний окіл точки  )(
)(  ). Тоді
). Тоді  . Але
. Але  , тобто
, тобто  - окіл точки
- окіл точки 
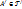 , і нехай
, і нехай  . Оскільки
. Оскільки  - окіл точки
- окіл точки  , тобто гомеоморфізм
, тобто гомеоморфізм  і
і  , звідки
, звідки  і
і  . Отже,
. Отже,  .
. – вимірною картою називають гомеоморфізм
– вимірною картою називають гомеоморфізм  відкритої підмножини
відкритої підмножини  на
на  (або на його відкриту підмножину). При цьому множину
(або на його відкриту підмножину). При цьому множину  інтервалів
інтервалів  з раціональними кінцями. За карту
з раціональними кінцями. За карту  (координатним околом цієї карти є
(координатним околом цієї карти є  та евклідів простір
та евклідів простір  також
також