 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Кривина та скрут просторової кривої. Тригранник Френе. Формули Френе.
Криві та поверхні в трьохвимірному евклідовому просторі, векторні параметризації. Елементарні поверхні. Означення: Множину точок, яку пробігає кінець радіус вектора при зміні параметра
Нехай функція Означення: Точку Означення: Крива, задана рівнянням Означення: Крива називається простою дугою, якщо існує ортонормований базис Теорема(про існування простої дуги): У кожній звичайній точці гладкої кривої існує окіл в якому вона є простою дугою. Означення: Дотичною в точці Теорема(про дотичну): У кожній звичайній точці гладкої кривої існує дотична, паралельна до Нехай регулярна крива 2-го порядку задана рівнянням Введемо ряд означень: Область Вектор-функція Поверхнею Ф називається годограф вектор-функції двох скалярних аргументів заданої на елементарній області Поверхня Ф називається елементарною, якщо вона гомеоморфна елементарній області Векторна рівність Приклад:
Означення: Параметризація поверхні Означення: поверхня називається простою в околі точки Означення: Точка Теорема: У кожній звичайній точці існує окіл в якому поверхня є простою Доведення:Ф: Кривина та скрут просторової кривої. Тригранник Френе. Формули Френе. Нехай рівнянням Напрямлений відрізок з початком в точці Означення: Скажемо, що в точці Означення: Площина Теорема: Якщо Якщо умова(*) не виконується і точка Означення: Точки кривої Означення: Нормаль в даній точці кривої, яка належить стичній площині називається головною нормаллю.
Означення: Площина, яка вданій точці містить бінормаль і головну нормаль називається нормальною площиною. Означення: Площина, яка в даній точці кривої містить бінормаль і дотичну називається спрямною площиною. Означення: Сукупність шести елементів: дотична, головна нормаль та бінормаль і 3 площини: стична, нормальна і спрямна називається тригранником Френе кривої Тригранник Френе утворює прямокутну просторову систему координат. Означення: Одиничні вектори Рівняння елементів тригранника Френе: 1. Рівняння дотичної: 2. Рівняння нормальної площини: 3. Рівняння бнормалі: 4. Рівняння стичної площини: 5. Рівняння головної нормалі: 6. Рівняння спрямної площини: Означення: Кривиною в данній точці кривої називається швидкість обертання в цій точці дотичної. Так як
Означення: Скрутом в данній точці кривої називається швидкість обертання в цій точці бінормалі. Так як
Означення: Точки кривої в яких кривина Теорема: Для того, щоб точка Теорема (Формули Френе): 1. 2. 3. Доведення :1. 3. 2. |



 на інтервалі
на інтервалі  називається годографом або кривою заданою рівнянням
називається годографом або кривою заданою рівнянням  . Крива – це деяка сукупність(множина) точок евклідового простору. Рівність
. Крива – це деяка сукупність(множина) точок евклідового простору. Рівність  - параметризація кривої в координатній формі.
- параметризація кривої в координатній формі. – параметричні рівняння кривої
– параметричні рівняння кривої , тоді
, тоді 
 називають звичайною для параметризації
називають звичайною для параметризації 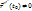 , і особливою, якщо умова
, і особливою, якщо умова  го порядку, якщо
го порядку, якщо  , тобто має
, тобто має  неперервних похідних. При
неперервних похідних. При  криву називають гладкою.
криву називають гладкою. в якому
в якому  ,
,  .
. при
при  .
. .
. ), причому
), причому  ,
,  .
. називається елементарною, якщо вона гомеоморфна відкритому кругу.
називається елементарною, якщо вона гомеоморфна відкритому кругу. називається вектор-функцією двох скалярних аргументів.
називається вектор-функцією двох скалярних аргументів. називається параметризацією поверхні.
називається параметризацією поверхні. ,
,  - не компланарні.
- не компланарні. 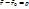 ,
,  ,
,  ,
,  ,
,  .
.  .
.  ,
,  ,
,  .
. ,
,  ,
,  - параболічний циліндр.
- параболічний циліндр. на елементарній області
на елементарній області  неперервних похідних на
неперервних похідних на  або
або  .
. , якщо існує окіл цієї точки
, якщо існує окіл цієї точки  в якому вона є елементарною. У цьому випадку її можна подати рівнянням
в якому вона є елементарною. У цьому випадку її можна подати рівнянням  .
. поверхні Ф називається звичайною, якщо в цій точці вектори
поверхні Ф називається звичайною, якщо в цій точці вектори  .
. ,
,  ,
,  . З теореми про неявні функції
. З теореми про неявні функції  що u=
що u=  . З параметричних рівнянь поверхні
. З параметричних рівнянь поверхні  .
. задано регулярну криву другого порядку
задано регулярну криву другого порядку  i
i  - довільна точка цієї кривої, яка відповідає значенню параметра
- довільна точка цієї кривої, яка відповідає значенню параметра  . Проведемо через точку
. Проведемо через точку  , визначивши її одиничним вектором
, визначивши її одиничним вектором  , ортогональним до неї. Змістимось по кривій
, ортогональним до неї. Змістимось по кривій 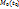 в точку
в точку  і оцінимо відстань точки
і оцінимо відстань точки  від площини
від площини  , опущеного з точки
, опущеного з точки  . Якщо
. Якщо  , то точка
, то точка  теж рухається до точки
теж рухається до точки  прямує до нуля, тобто є нескінченно малою величиною разом з
прямує до нуля, тобто є нескінченно малою величиною разом з  є нескінченно малою не нижче третього порядку малості відносно
є нескінченно малою не нижче третього порядку малості відносно  при
при  в точці
в точці  (*) ,то в точці
(*) ,то в точці  .
. , то будь-яка площина, що містить в собі дотичну до цієї кривої в точці
, то будь-яка площина, що містить в собі дотичну до цієї кривої в точці  Означення:Нормаль в даній точці кривої до стичної площини називається бінормаллю.
Означення:Нормаль в даній точці кривої до стичної площини називається бінормаллю. , які розташовані відповідно
, які розташовані відповідно  на дотичній,
на дотичній,  на головній нормалі,
на головній нормалі,  на бінормалі права трійка векторів.
на бінормалі права трійка векторів.  .
.  ,
,  ,
,  ,
,  ,
,  .
. .
. .
. .
. .
. .
. , де
, де 
 колінеарний дотичній , то кривина це швидкість обертання
колінеарний дотичній , то кривина це швидкість обертання  , де
, де  - кут між двома дотичними.
- кут між двома дотичними. , де
, де  - кут між двома бінормалями.
- кут між двома бінормалями. називаються точками розпрямлення.
називаються точками розпрямлення. була точкою розпрямлення необхідно і досить, щоб
була точкою розпрямлення необхідно і досить, щоб  .
. ,
, ,
, , де
, де  - скрут кривої.
- скрут кривої. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
, 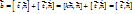 ,
, 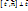 ,
,  ,
,  ,
,  .
. ,
, 