 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Перша квадратична форма (ПКФ) поверхні, її застосування.
5. Першою квадратичною формою гладкої поверхні Ф з векторною параметризацією  , називають вираз , називають вираз  , де , де
 , ,
 , ,
 . .
Оскільки  ( (  - повний диференціал поверхні), і поверхня Ф не містить особливих точок, то ця квадратична форма є додатно визначеною і обертається в нуль лише при - повний диференціал поверхні), і поверхня Ф не містить особливих точок, то ця квадратична форма є додатно визначеною і обертається в нуль лише при  . . Застосуємо ПКФ для знаходження довжини дуги кривої на поверхні, кута між кривими на поверхні та обчислення площі області на поверхні. Задамо на поверхні Ф довільну регулярну криву  : :  , дуга якої , дуга якої  має довжину має довжину  , що визначається формулою , що визначається формулою  . Тоді маємо . Тоді маємо  , де , де  - ПКФ поверхні Ф. - ПКФ поверхні Ф. Рівнянням  визначимо на цій поверхні ще одну гладку криву визначимо на цій поверхні ще одну гладку криву  . Нехай криві . Нехай криві  і і  мають спільну точку М( мають спільну точку М(  ). Під кутом між цими кривими в точці М ми розуміємо кут ). Під кутом між цими кривими в точці М ми розуміємо кут  між їх дотичними в цій точці. Знайдемо цей кут, відшукавши кут між напрямними векторами між їх дотичними в цій точці. Знайдемо цей кут, відшукавши кут між напрямними векторами  і і  цих дотичних: цих дотичних: 
Для знаходження кута між координатними лініями поверхні Ф в точці М в останній формулі покладемо, наприклад,  і одержимо і одержимо  .приходимо до висновку, що координатна сітка поверхні є ортогональною(її координатні лінії перетинаються під прямим кутом) тоді і тільки тоді, коли .приходимо до висновку, що координатна сітка поверхні є ортогональною(її координатні лінії перетинаються під прямим кутом) тоді і тільки тоді, коли  для всіх точок для всіх точок  . . Припустимо, що D – область з  , обмежена кусково-гладким контуром, а Г – годограф гладкої вектор-функції , обмежена кусково-гладким контуром, а Г – годограф гладкої вектор-функції  на множині D. на множині D. Означимо поняття площі області Г. для цього розіб’ємо цю область сіткою координатних ліній на криволінійні паралелограми. Розглянемо один з них, позначивши його вершини через  , ,  , ,  , , 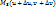 , таким чином, щоб , таким чином, щоб  та та  були додатними. Замінимо цей паралелограм, побудованим на напрямлених відрізках були додатними. Замінимо цей паралелограм, побудованим на напрямлених відрізках  та та  з початками в точці М( з початками в точці М(  ) як на сторонах. Зрозуміло, що останній паралелограм лежить в дотичній площині до поверхні Ф в точці М( ) як на сторонах. Зрозуміло, що останній паралелограм лежить в дотичній площині до поверхні Ф в точці М(  ). Його площу ). Його площу  знайдемо за формулою знайдемо за формулою  . Але з рівності . Але з рівності  випливає, що випливає, що  , отже , отже  , де коефіцієнти , де коефіцієнти  обраховано в точці М( обраховано в точці М(  ). ). Зауваження: Вираз  називають дискримінантом ПКФ поверхні Ф. Зрозуміло, що він не може набувати від’ємних значень і перетворюватися в 0. називають дискримінантом ПКФ поверхні Ф. Зрозуміло, що він не може набувати від’ємних значень і перетворюватися в 0. Аналогічно поступимо з кожним криволінійним паралелограмом здійсненого розбиття і складемо суму площ усіх одержаних прямолінійних паралелограмів:  . .
Означення: Якщо існує границя, яка не залежить ні від способу розбиття області Г координатними лініями, ні від вибору параметризації поверхні Ф, то цю границю назвемо площею області Г. Оскільки  є неперервна функція від є неперервна функція від  та та  , то вказана границя існує і не залежить від способу розбиття області Г на криволінійній паралелограми, причому , то вказана границя існує і не залежить від способу розбиття області Г на криволінійній паралелограми, причому  . (*) . (*)
Залишилось показати, що одержана величина не залежить від вибору параметризації поверхні Ф. Для цього перейдемо до довільної її еквівалентної параметризації 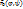 . Використавши означення еквівалентних параметризацій отримаємо . Використавши означення еквівалентних параметризацій отримаємо  , звідки маємо , звідки маємо  , де , де 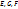 - коефіцієнти ПКФ поверхні в криволінійних координатах - коефіцієнти ПКФ поверхні в криволінійних координатах  . Тоді вираз (*) набирає вигляду . Тоді вираз (*) набирає вигляду 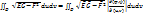 . Скориставшись формулою заміни змінних в подвійному інтегралі одержуємо рівність . Скориставшись формулою заміни змінних в подвійному інтегралі одержуємо рівність  , в якій через , в якій через  позначено область, гомеоморфні області позначено область, гомеоморфні області  при переході до параметризації при переході до параметризації 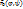 . . Адитивність площі поверхні випливає з адитивності подвійного інтеграла, тобто  . При обчисленні площі поверхні можна розбивати цю поверхню на частини і для кожної з них використовувати свою параметризацію. . При обчисленні площі поверхні можна розбивати цю поверхню на частини і для кожної з них використовувати свою параметризацію.
|




 , називають вираз
, називають вираз , де
, де ,
, ,
, .
. (
(  - повний диференціал поверхні), і поверхня Ф не містить особливих точок, то ця квадратична форма є додатно визначеною і обертається в нуль лише при
- повний диференціал поверхні), і поверхня Ф не містить особливих точок, то ця квадратична форма є додатно визначеною і обертається в нуль лише при  .
. :
:  , дуга якої
, дуга якої  має довжину
має довжину  , що визначається формулою
, що визначається формулою  . Тоді маємо
. Тоді маємо  , де
, де  - ПКФ поверхні Ф.
- ПКФ поверхні Ф. визначимо на цій поверхні ще одну гладку криву
визначимо на цій поверхні ще одну гладку криву  . Нехай криві
. Нехай криві  ). Під кутом між цими кривими в точці М ми розуміємо кут
). Під кутом між цими кривими в точці М ми розуміємо кут  між їх дотичними в цій точці. Знайдемо цей кут, відшукавши кут між напрямними векторами
між їх дотичними в цій точці. Знайдемо цей кут, відшукавши кут між напрямними векторами  цих дотичних:
цих дотичних:
 і одержимо
і одержимо  .приходимо до висновку, що координатна сітка поверхні є ортогональною(її координатні лінії перетинаються під прямим кутом) тоді і тільки тоді, коли
.приходимо до висновку, що координатна сітка поверхні є ортогональною(її координатні лінії перетинаються під прямим кутом) тоді і тільки тоді, коли  для всіх точок
для всіх точок  .
. , обмежена кусково-гладким контуром, а Г – годограф гладкої вектор-функції
, обмежена кусково-гладким контуром, а Г – годограф гладкої вектор-функції  на множині D.
на множині D. ,
,  ,
,  ,
, 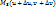 , таким чином, щоб
, таким чином, щоб  та
та  були додатними. Замінимо цей паралелограм, побудованим на напрямлених відрізках
були додатними. Замінимо цей паралелограм, побудованим на напрямлених відрізках  та
та  з початками в точці М(
з початками в точці М(  знайдемо за формулою
знайдемо за формулою  . Але з рівності
. Але з рівності  випливає, що
випливає, що  , отже
, отже  , де коефіцієнти
, де коефіцієнти  обраховано в точці М(
обраховано в точці М(  називають дискримінантом ПКФ поверхні Ф. Зрозуміло, що він не може набувати від’ємних значень і перетворюватися в 0.
називають дискримінантом ПКФ поверхні Ф. Зрозуміло, що він не може набувати від’ємних значень і перетворюватися в 0. .
. є неперервна функція від
є неперервна функція від  та
та  , то вказана границя існує і не залежить від способу розбиття області Г на криволінійній паралелограми, причому
, то вказана границя існує і не залежить від способу розбиття області Г на криволінійній паралелограми, причому . (*)
. (*)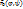 . Використавши означення еквівалентних параметризацій отримаємо
. Використавши означення еквівалентних параметризацій отримаємо  , звідки маємо
, звідки маємо  , де
, де 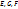 - коефіцієнти ПКФ поверхні в криволінійних координатах
- коефіцієнти ПКФ поверхні в криволінійних координатах  . Тоді вираз (*) набирає вигляду
. Тоді вираз (*) набирає вигляду 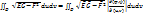 . Скориставшись формулою заміни змінних в подвійному інтегралі одержуємо рівність
. Скориставшись формулою заміни змінних в подвійному інтегралі одержуємо рівність  , в якій через
, в якій через  позначено область, гомеоморфні області
позначено область, гомеоморфні області  при переході до параметризації
при переході до параметризації  . При обчисленні площі поверхні можна розбивати цю поверхню на частини і для кожної з них використовувати свою параметризацію.
. При обчисленні площі поверхні можна розбивати цю поверхню на частини і для кожної з них використовувати свою параметризацію.