 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теорія площин у просторі (аналітичний виклад).
Нехай в просторі задана загальна система координат x, y, z – змінних. О. Рівнянням від трьох змінних x, y, z наз. рівняння f(x, y, z)=0. F(x, y, z)=0- деякий аналітичний вираз, що одночасно не перетворюється в 0 при всіх значеннях змінних x, y, z . Якщо ж рівність (1) f(x, y, z)=0 справджується при всіх змінних, то
б) Нехай δ задана трьома точками в) Площина може задаватись також трьома точками, розташованими в системі координат Т. В загальній декартові системі координат площину записують рівнянням першого степеня, виду ax+by+cz+d=0.
Т. Довільне рівняння першого степеня Часткові випадки розташування площин. Д=0 С=0. Тоді нормальний вектор n(А,В,0) він перпендикулярний до OZ. Площина σ ║OZ. В=0 Рівняння площини, що проходить через три точки.
Параметричне рівняння площини.
Нормальне рівняння площини Зведення загального рівняння площини до загального.
О. Відхиленням т. Т. Відхилення т. Взаємне розташування площин Т. Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг розташованої матриці системи дорівняє рангу основної матриці. О. Пучком площин назив. сукупність тих і тільки тих площин простору, що проходять через одну пряму – вісь пучка. Т. Якщо в площині декартової системи координат задані дві площини О. В’язкою площин наз. сукупність тих і тільки тих площин простору, що проходять через одну і ту ж точку, яка наз. центром в’язки. Теорія прямих в просторі Нехай в просторі задано прям. декартову сис. коорд., відносно неї розміщена пряма У записі (1) є 2 р-ня Прикладом є параметричне р-ня прямої, утв. з (1) прирівнявши кожне відношення до Зручно використовувати для знаходження такого перетину прямої і площини, р-ня прямої, що проходить через 2 т. Вище говорилося, що пряма утв. як перетин 2-х площин. Нехай Сис. (*) наз. загальним р-ням прямої. Зведемо його до канонічного виду. Для знаходження напрямленого Прямі в площині перетинаються, якщо: |



 вона наз. тотожністю.
вона наз. тотожністю.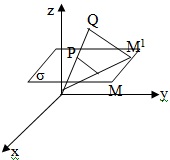
 О. Поверхнею наз. ГМТ простору, координати яких в деякій системі координат задов. рівняння (1). Найпростіші із поверхонь є площини. Розглянемо можливі задання площин.
О. Поверхнею наз. ГМТ простору, координати яких в деякій системі координат задов. рівняння (1). Найпростіші із поверхонь є площини. Розглянемо можливі задання площин. а) Нехай задано т.
а) Нехай задано т.  і два не колінеарні вектори а і b ║δ, тоді т.
і два не колінеарні вектори а і b ║δ, тоді т.  і
і  визначають площину в просторі. Нехай точка М має такі координати
визначають площину в просторі. Нехай точка М має такі координати  ,
,  ,
,  . В такому разі трьома числами характеризується площина в просторі. Точка М – початкова точка площини, а і b – напрямні вектори.
. В такому разі трьома числами характеризується площина в просторі. Точка М – початкова точка площини, а і b – напрямні вектори. ,
,  ,
, 
 . Площина задана дев’ятьма числами.
. Площина задана дев’ятьма числами. .
. Дов.: Зафіксуємо на площині σ довільну точку
Дов.: Зафіксуємо на площині σ довільну точку  та виберемо на ній два не колінеарні вектори
та виберемо на ній два не колінеарні вектори  і
і  .
.  ,
,  ,
,  . Нехай довільна точка М площини σ має координати
. Нехай довільна точка М площини σ має координати  .
.  ,
,  =0 (2)
=0 (2) 
 ,
,  Покажемо, що А=В=С≠0.
Покажемо, що А=В=С≠0.  Ці числа будуть пропорційні, а це неможливо.
Ці числа будуть пропорційні, а це неможливо. в загальній Декартові системі координат задає рівняння площини.
в загальній Декартові системі координат задає рівняння площини. - площина проходить через точку О(0;0).
- площина проходить через точку О(0;0). σ ║OY. 4)А=0
σ ║OY. 4)А=0 
 Нехай в просторі площина визначається трьома точками
Нехай в просторі площина визначається трьома точками  . Аналогічно
. Аналогічно  і
і 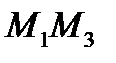 . Маємо визначник:
. Маємо визначник: 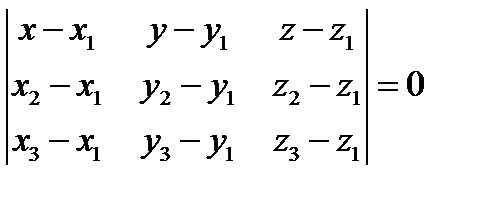 (1) – Рівняння площини, що проходить через три точки.
(1) – Рівняння площини, що проходить через три точки. Нехай площина σ задана т.
Нехай площина σ задана т.  . Тоді
. Тоді  будуть компланарні. Оскільки а непаралельне b,
будуть компланарні. Оскільки а непаралельне b,  можна подати через два не компланарні вектори
можна подати через два не компланарні вектори  .
.
 - параметричне рівняння площини.
- параметричне рівняння площини. .
. ,
, ,
,
 . Знак не повинен бути протилежним до вільного члена р.
. Знак не повинен бути протилежним до вільного члена р. від площини σ назив. додатнє число δ=d, якщо т.
від площини σ назив. додатнє число δ=d, якщо т.  і початок координат розміщені по різні боки від площини і δ=-d, якщо по один бік.
і початок координат розміщені по різні боки від площини і δ=-d, якщо по один бік. ,
,  .
. і
і  загальними рівняннями і ці площини перетинаються по прямій l, то
загальними рівняннями і ці площини перетинаються по прямій l, то  .
. . Нехай т.
. Нехай т.  ,
,  — напрямлений вектор прямої
— напрямлений вектор прямої  ,
,  — біжуча точка.
— біжуча точка.  парал до
парал до 
 (1) — р-ня прямої
(1) — р-ня прямої  .
. , що є р-ням площини, тоді пряма утворена як перетин площин і (1) наз. канонічними р-нями.
, що є р-ням площини, тоді пряма утворена як перетин площин і (1) наз. канонічними р-нями. .
.  .
. і
і  :
: 
 (*)
(*) досить знайти
досить знайти  — век. добуток (за озн):
— век. добуток (за озн): 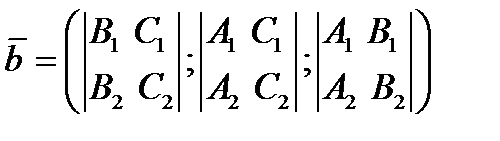
 будемо мати р-ня:
будемо мати р-ня:  , де
, де  . Є поняття кута між прямими в просторі – це кут між їх напрямленими век., або кут, що доповнює його до
. Є поняття кута між прямими в просторі – це кут між їх напрямленими век., або кут, що доповнює його до  . Коли маємо 2 прямі
. Коли маємо 2 прямі  і
і  і їх напрямлені век.
і їх напрямлені век.  та
та  , відповідно, то
, відповідно, то  прямі ортогональні
прямі ортогональні 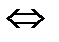
 ,
, 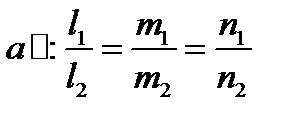 .
. . 2-3 рядки пропорційні.
. 2-3 рядки пропорційні.