Група рухів площини та її підгрупи. Застосування до розв’язування задач на побудову.
О. Перетворення площини, при якому зберігається відстані наз. рухом площини. Нехай в площ.  задано трикутник задано трикутник  і вказано напрямок обходу вершини цього трикутника (від А до С через В), тоді такий трикутник і така площ. наз. орієнтованими. Додатня орієнтація — це проти руху годинникової стрілки. Якщо рух переводить орієнтовану площ. в площ. з тією ж орієнтацією, то такий рух наз. рухом 1-го роду. Якщо ж орієнтація міняється на протилежну, то — рухом 2-го роду. Послідовне виконання двох рухів наз. композицією. і вказано напрямок обходу вершини цього трикутника (від А до С через В), тоді такий трикутник і така площ. наз. орієнтованими. Додатня орієнтація — це проти руху годинникової стрілки. Якщо рух переводить орієнтовану площ. в площ. з тією ж орієнтацією, то такий рух наз. рухом 1-го роду. Якщо ж орієнтація міняється на протилежну, то — рухом 2-го роду. Послідовне виконання двох рухів наз. композицією. Вл. руху 1) Рух є взаємнооднозначна відповідність між точками площ. 2) До  руху руху  одиничний обернений одиничний обернений 3) Послідовне виконання 2-х рухів знову рух І або ІІ роду 4) Рух переводить пряму в пряму, парал прямі в парал прямі 5) Рух переводить півплощини з межею  в півплощини з межею в півплощини з межею  , де , де  — образ прямої — образ прямої  при цьому русі при цьому русі 6) Рух зберігає просте відношення трьох точок прямої 7) Рух зберігшє поняття «лежати між» 8) Рух переводить промінь з початком в т. А в проммінь з початком в т.  , яка є образом т. А при цьому русі , яка є образом т. А при цьому русі 9) Рух переводить відрізок  в відрізок в відрізок  , відповідно образи т. А і В , відповідно образи т. А і В 10) Рух переводить кут в кут, рівні кути в рівні. 11) Рух переводить  прямі в прямі в  прямі прямі Множина всіх рухів, що задовільняють вл. 1-11 утв. групу відносно відносно операції композиція. О. Групою 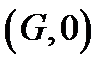 будемо наз. пару будемо наз. пару 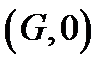 , де G — непорожня мн., якщо виконуються умови: , де G — непорожня мн., якщо виконуються умови: 1) замкненість операції:  2) асоціативність операції композиція:  3)  -ня нейтрального елемента: -ня нейтрального елемента:  4)  -ня симетричного елемента: -ня симетричного елемента: 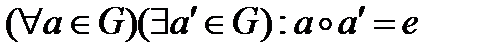 О. Якщо  і пара і пара  утв. групу, то групу утв. групу, то групу  наз. підгрупою групи G. наз. підгрупою групи G. Доведемо,що множина всіх рухів площини утв. групу 1)  2) 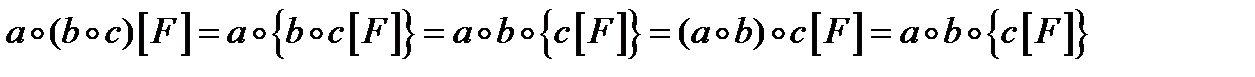 Нейтральним елементом G буде рух, який переводить  т. площини т. площини  в себе. в себе. Оскільки  рух — це взаємнооднозначна відповіднвсть між точками площини, то завжди рух — це взаємнооднозначна відповіднвсть між точками площини, то завжди  рух обернений до рух обернений до  руху мн. руху мн.  . Отже, множина всіх рухів площини утв. групу. . Отже, множина всіх рухів площини утв. групу. Рухи 1-го роду: 1) перенесення, повороти. 2) осьова симетрія, ковзаюча симетрія. Перетворення площини, яке кожну точку  цієї площини переводить в т. цієї площини переводить в т.  цієї ж площини, таку, що вектор цієї ж площини, таку, що вектор  наперед заданому вектору наперед заданому вектору  наз. наз.  перенесення площини. перенесення площини. Поворот: Нехай осі  і і  двох осьових симетрій утв. кут двох осьових симетрій утв. кут  . Нехай . Нехай  т. площини т. площини  . .  Якщо т. Якщо т.  симетрична відносно осі симетрична відносно осі  , а , а  симетрична з симетрична з  відносно відносно 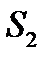 , то , то  , ,  , т. , т.  отримано з т. отримано з т.  в наслідок руху 1-го роду, який має вл.: в наслідок руху 1-го роду, який має вл.:  , ,  , де , де 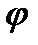 — менша з 2-х кутів, утв. — менша з 2-х кутів, утв.  і і  . Такий рух наз. поворотом на кути. Множина всіх поворотів пл. Відносно заданої т. утв. групу, яка є підгрупою групи всіх . Такий рух наз. поворотом на кути. Множина всіх поворотів пл. Відносно заданої т. утв. групу, яка є підгрупою групи всіх 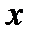 перетворень площини. перетворень площини.
Осьова симетрія: Будемо казати, що т.  і і  симетричні відноснопрямої симетричні відноснопрямої  , якщо відрізок , якщо відрізок  і ділиться нею пополам. Фігури і ділиться нею пополам. Фігури 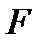 і і  наз. симетричні відносно прямої наз. симетричні відносно прямої  , якщо відповідні точки цих фігур симетричні відносно прямої , якщо відповідні точки цих фігур симетричні відносно прямої  . . Перетворення площини буде рухом, який наз. ковзаючою симетрією, якщо вона представлена у вигляді послідовного виконання рухів.  Осьова симетрія Осьова симетрія
Приклад. На даній прямій побудуємо т.  так, щоб ламана так, щоб ламана  мала найменшу довжину, точки мала найменшу довжину, точки 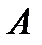 і і  лежать по один бік від даної прямої. лежать по один бік від даної прямої. Нехай 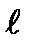 — дана пряма, — дана пряма, 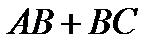 має найменшу довжину. Нехай т. має найменшу довжину. Нехай т.  симетрична відносно симетрична відносно 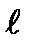 з т. з т.  . Якщо . Якщо  , то , то  — шукана. Дійсно: — шукана. Дійсно:  , ,  . Дослідження: т. . Дослідження: т.  завжди завжди  , а , а  завжди перетинає пряму завжди перетинає пряму 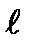 в єдиній точці, то задача має і до того тільки один розв’язок. в єдиній точці, то задача має і до того тільки один розв’язок. Рухи можна застосовувати до розв задач на побудову. Припустимо, що задача розв., тобто шукана фігура побуд. До окремих частин фігури або до всієї шуканої фігури застос певне перетворення і цим сами розв даної задачі зводимо до розв деякої допоміжної задачі, яка як правило набагато простіша за вихідну. Розв’язавши цю задачу викон обернене перетворення і тим самим одерж розв даної задачі.
| 



 задано трикутник
задано трикутник  і вказано напрямок обходу вершини цього трикутника (від А до С через В), тоді такий трикутник і така площ. наз. орієнтованими. Додатня орієнтація — це проти руху годинникової стрілки. Якщо рух переводить орієнтовану площ. в площ. з тією ж орієнтацією, то такий рух наз. рухом 1-го роду. Якщо ж орієнтація міняється на протилежну, то — рухом 2-го роду. Послідовне виконання двох рухів наз. композицією.
і вказано напрямок обходу вершини цього трикутника (від А до С через В), тоді такий трикутник і така площ. наз. орієнтованими. Додатня орієнтація — це проти руху годинникової стрілки. Якщо рух переводить орієнтовану площ. в площ. з тією ж орієнтацією, то такий рух наз. рухом 1-го роду. Якщо ж орієнтація міняється на протилежну, то — рухом 2-го роду. Послідовне виконання двох рухів наз. композицією. руху
руху  одиничний обернений
одиничний обернений в півплощини з межею
в півплощини з межею  , де
, де  , яка є образом т. А при цьому русі
, яка є образом т. А при цьому русі в відрізок
в відрізок  , відповідно образи т. А і В
, відповідно образи т. А і В прямі в
прямі в 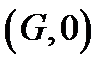 будемо наз. пару
будемо наз. пару 

 -ня нейтрального елемента:
-ня нейтрального елемента: 
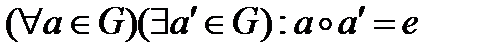
 і пара
і пара  утв. групу, то групу
утв. групу, то групу  наз. підгрупою групи G.
наз. підгрупою групи G.
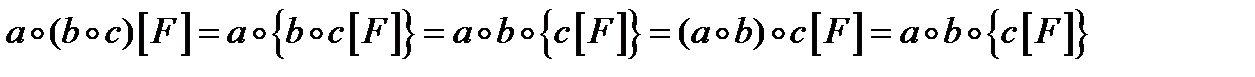
 т. площини
т. площини  в себе.
в себе. . Отже, множина всіх рухів площини утв. групу.
. Отже, множина всіх рухів площини утв. групу. цієї площини переводить в т.
цієї площини переводить в т.  цієї ж площини, таку, що вектор
цієї ж площини, таку, що вектор  наперед заданому вектору
наперед заданому вектору  наз.
наз.  перенесення площини.
перенесення площини. і
і  двох осьових симетрій утв. кут
двох осьових симетрій утв. кут  . Нехай
. Нехай  т. площини
т. площини  .
. Якщо т.
Якщо т.  симетрична відносно осі
симетрична відносно осі  , а
, а  симетрична з
симетрична з 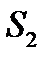 , то
, то  ,
,  , т.
, т.  отримано з т.
отримано з т.  в наслідок руху 1-го роду, який має вл.:
в наслідок руху 1-го роду, який має вл.:  ,
, 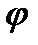 — менша з 2-х кутів, утв.
— менша з 2-х кутів, утв. 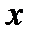 перетворень площини.
перетворень площини. і
і  симетричні відноснопрямої
симетричні відноснопрямої  , якщо відрізок
, якщо відрізок  і ділиться нею пополам. Фігури
і ділиться нею пополам. Фігури 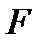 і
і  наз. симетричні відносно прямої
наз. симетричні відносно прямої  Осьова симетрія
Осьова симетрія так, щоб ламана
так, щоб ламана  мала найменшу довжину, точки
мала найменшу довжину, точки 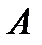 і
і  лежать по один бік від даної прямої.
лежать по один бік від даної прямої.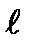 — дана пряма,
— дана пряма, 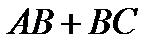 має найменшу довжину. Нехай т.
має найменшу довжину. Нехай т.  симетрична відносно
симетрична відносно  , то
, то  ,
,  . Дослідження: т.
. Дослідження: т.  , а
, а  завжди перетинає пряму
завжди перетинає пряму