Система координат в 3-вимірному просторі. Перетворення системи координат.
Скалярний і векторний добуток двох векторів, їх властивості та застосування. Нехай  і і  ненульові вектори. Якщо розмістити ці вектори на прямих паралельних до кожного з них і задати напрямок, що співпадає з напрямком векторів, то отримаєм дві напрямлені прямі, які в загальному випадку не перетнуться. ненульові вектори. Якщо розмістити ці вектори на прямих паралельних до кожного з них і задати напрямок, що співпадає з напрямком векторів, то отримаєм дві напрямлені прямі, які в загальному випадку не перетнуться. О. Кутом між напрямленими прямими назвемо менший з двох кутів, які вони утворюють.  О. Під кутом між 2-ма векторами будемо розуміти кут між напрямленими прямими  . . О. Число  будемо називати скалярним добутком векторів будемо називати скалярним добутком векторів  , якщо воно , якщо воно   . Якщо скал добуток =0, то ці вектори перпендикулярні або один з них 0-вектор. . Якщо скал добуток =0, то ці вектори перпендикулярні або один з них 0-вектор.  Т. Скалярний добуток двох векторів, заданих своїми координатами відносно ортонормованої бази = сумі добутків відповідних координат цих векторів: Т. Скалярний добуток двох векторів, заданих своїми координатами відносно ортонормованої бази = сумі добутків відповідних координат цих векторів:  (1). (1).
Д. Нехай  – не колінеарні і не нульові. Виберемо точку О і відкладемо вектори – не колінеарні і не нульові. Виберемо точку О і відкладемо вектори  . Розглянемо . Розглянемо  . За теоремою косинусів: . За теоремою косинусів:  
або    (2) (2)
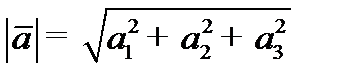 ; ;  , ,  , тоді , тоді  . Підставимо одержані рез-ти в (2), маємо: . Підставимо одержані рез-ти в (2), маємо:   
 . Теорему доведено. . Теорему доведено.
Т. Для довільного дійсного  і дов векторів і дов векторів  мають місце співвідношення: мають місце співвідношення: 1) 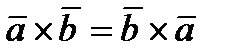 — комутативність — комутативність 2)  — сполучна — сполучна  3)  — розподільна — розподільна Д. 1)    2)  = =   . Т. д. . Т. д. Скалярний добуток застосов. для виявлення ортогональних прямих в евклідовому просторі. О. Векторний добуток в-ра  на на  називається вектор називається вектор  , такий що задовільняє умовам: , такий що задовільняє умовам: 1)   ; ; 2)  і і  ; ; 3)  утворюють праву трійку. Позначабть век доб утворюють праву трійку. Позначабть век доб  . . Т.1.(Геом власт векторного добутку) Векторний добуток двох не нульових векторів =0 тоді і тільки тоді, коли ці вектори колінеарні. Д. 1)  і і  - колінеарні. Можливі випадки: - колінеарні. Можливі випадки:  =0 і =0 і  =180. В обох випадках sin цих кутів =0. Тому =180. В обох випадках sin цих кутів =0. Тому   =0 Отже, век доб цих векторів =0. =0 Отже, век доб цих векторів =0. 2) Нехай век доб цих векторів =0. Тоді   =0. Це можливо тоді, коли sin =0. Це можливо тоді, коли sin  =0. Тому =0. Тому  =0 або 180. Звідки =0 або 180. Звідки  і і  колінеарні. колінеарні. Т2. Якщо вектори  і і  зведені до спільного початку, то модуль векторного добутку = площі паралелограма побудованого на цих векторах, як на сторонах (геом зміст). зведені до спільного початку, то модуль векторного добутку = площі паралелограма побудованого на цих векторах, як на сторонах (геом зміст). 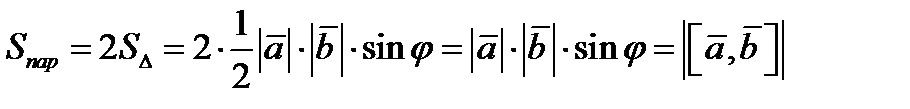 Справедливість теореми випливає з формули  . . Алгебраїчні властивості Антикомутативна:  = =  . . Сполучна відносно скалярного множника 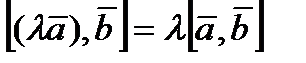 , ,  . . Дистрибутивна властивість відносно 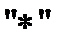 відносно відносно   Т. Якщо Т. Якщо  і і  задані своїми координатами задані своїми координатами  то відносно базису то відносно базису 
 = = 
Д.   
Т.д. Застосування.  : у фізиці — механічна робота, магнітний потік. : у фізиці — механічна робота, магнітний потік.  : момент сили, тангенціальна та кутова поверхні. : момент сили, тангенціальна та кутова поверхні. О. Мішаним або векторно-скалярним добутком 3 впорядкованих векторів  , ,  і і  наз. Скалярний добуток вектора наз. Скалярний добуток вектора  на вектор на вектор  . .     . .
Т.Якщо  , ,  , ,  задані своїми координатами задані своїми координатами  , ,  в ортонормованому базисі, то їх мішаний добуток = визначнику 3-го порядку, рядками якого є координати цих векторів. в ортонормованому базисі, то їх мішаний добуток = визначнику 3-го порядку, рядками якого є координати цих векторів. Д. 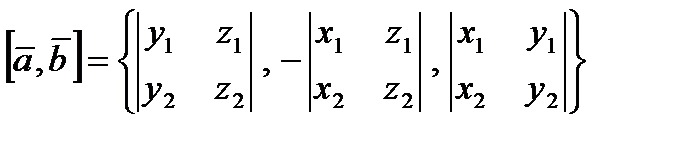 . . 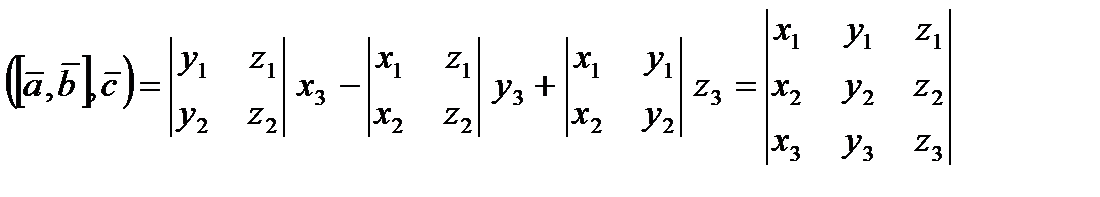 Т. Абсолютна величина мішаного добутку трьох векторів = об’єму паралелепіпеда, побудованого на них, віднесених до спільного початку. При цьому  , якщо трійка , якщо трійка  , ,  , ,  - права, - права, 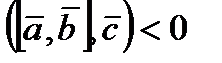 , якщо трійка , якщо трійка  , ,  , ,  - ліва і - ліва і  0, якщо 0, якщо  , ,  , ,  - компланарні. - компланарні. Система координат в 3-вимірному просторі. Перетворення системи координат. Візьмемо довільну точку О і  базис базис  простору. Ця четвірка наз афінною сис координат в 3-вимірному просторі простору. Ця четвірка наз афінною сис координат в 3-вимірному просторі  . (1) . (1) Точка О — початок координат, а  координатні вектори. Напрямлені прямі, що проходять через початок координат і паралельні коорд векторам, на яких додатній напрям визначається цими векторами, наз коорд осями. Це осі абсцис, ординат і аплікат координатні вектори. Напрямлені прямі, що проходять через початок координат і паралельні коорд векторам, на яких додатній напрям визначається цими векторами, наз коорд осями. Це осі абсцис, ординат і аплікат  . Площини, що визначаються поч коорд і осями . Площини, що визначаються поч коорд і осями  наз координатними площинами і позначаються наз координатними площинами і позначаються  . . Нехай т М —  т простору. Вектор т простору. Вектор  — радіус-вектор т М відносно О. Координати — радіус-вектор т М відносно О. Координати  в-ра в-ра  в базисі в базисі  наз координатами т М. наз координатами т М. Число  – абсциса, – абсциса, 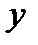 – ордината, – ордината,  – апліката. Пишуть т – апліката. Пишуть т  : :  . Для побудови т . Для побудови т  в системі в системі  за її коорд користуються формулою: за її коорд користуються формулою:  . Від початку координат відкладають вектор . Від початку координат відкладають вектор  , від точки , від точки  відладають век відладають век  і від точки і від точки  — —  . За правилами многокутника: . За правилами многокутника:  . М — шукана точка. . М — шукана точка. Ламану  наз коорд ламаною. Якщо виконується рівність: наз коорд ламаною. Якщо виконується рівність:  . Век . Век 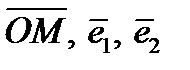 лінійно залежні, тому колінеарні. Це означає, що т лінійно залежні, тому колінеарні. Це означає, що т  . . Аналогічно  , то , то   що що  т осі абсцис т осі абсцис  . .  т осі ординат т осі ординат  . .  т осі аплікат т осі аплікат  . . Кожна координата вектора = різниці відповідних координат кінця і початку вектора. Нехай 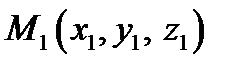 і і  , то , то  : :  , де , де  — точка, що ділить відрізок — точка, що ділить відрізок  у відношенні у відношенні  . .  . .  Сис коорд наз прямокутною декартовою або декартовою, якщо базис цієї сис є ортонормованим. Таку сис коорд з початком в т О позначають так: Сис коорд наз прямокутною декартовою або декартовою, якщо базис цієї сис є ортонормованим. Таку сис коорд з початком в т О позначають так:  або або  , де , де  . .  . Нехай в прямокутній сис коорд . Нехай в прямокутній сис коорд  задано т. задано т.  і і  , які мають координати , які мають координати 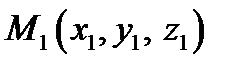 і і  . Обчислим відстань між ними. Оскільки за формулою . Обчислим відстань між ними. Оскільки за формулою  , то враховуючи, що , то враховуючи, що 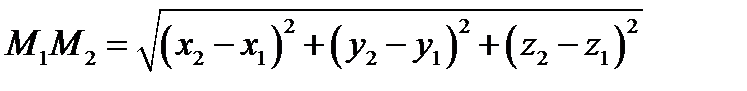  : : 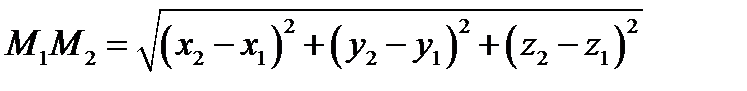 . .
Формули переходу.  Розглянемо в просторі дві афінні сис коорд Розглянемо в просторі дві афінні сис коорд  і і  . Нехай . Нехай  т простору: в старій сис т простору: в старій сис  , в новій , в новій  . Завдання полягає в тому щоб, знаючи . Завдання полягає в тому щоб, знаючи  , ,  , ,  , ,  (1) в старій сис виразити координати (1) в старій сис виразити координати  т М через т М через  тієї ж точки М в новій системі. За озн. коорд. в-рів з (1): тієї ж точки М в новій системі. За озн. коорд. в-рів з (1):  . За правилом трикутника: . За правилом трикутника:  , ,  , ,  , ,  ; (2) ; (2)

Ф-ли (3) наз. ф-лами перетворення афінної сис. координат. З цих ф-мул отримуючи ф-ли перетворення координат при переході від  до до  . . 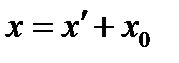 , ,  , ,  - ф-ли парал. перенесення. - ф-ли парал. перенесення.
 , ,  , ,  - ф-ли при повороті. - ф-ли при повороті.
Розглянемо перет. прямок. сис. коорд. При переході від  до іншої до іншої  , можна використати ф-ли (3). Матриця переходу від базису , можна використати ф-ли (3). Матриця переходу від базису  до до  має вигляд: має вигляд:  . . Сума квадратів кожного рядка матриці  , сума добутків відповідних елем. , сума добутків відповідних елем.  2-х її різних стовпців =0, така матриця наз. ортогональною. 2-х її різних стовпців =0, така матриця наз. ортогональною. Теорія прямих на площині. Напрямленим вектором прямої будемо наз. довільний ненульвий в-тор паралельний до цієї прямої. На прямій  виберемо довільну т. М , яка наз. біжучою т. прямої. В-ри виберемо довільну т. М , яка наз. біжучою т. прямої. В-ри  і і  компланарні. Їх коорд. пропорційні компланарні. Їх коорд. пропорційні  (1) (1)    — загальне рівняння прямої. — загальне рівняння прямої.  Рівняння прямої задане напрямленим вектором, яка проходить через задану точку має вигляд: Рівняння прямої задане напрямленим вектором, яка проходить через задану точку має вигляд:  . .
Т. Для того, щоб пряма задана заг. р-ням проходила через поч. коорд. Н. і Д. , щоб  . .  Д. 1) Д. 1)  . Поч. коорд. належить цій прямій. З другого боку, якщо пряма . Поч. коорд. належить цій прямій. З другого боку, якщо пряма 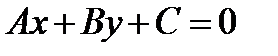 проходить через поч. коорд. тоді і т. проходить через поч. коорд. тоді і т.  задовільняє цю рівність, а це можливо тоді коли задовільняє цю рівність, а це можливо тоді коли  . .
2)  — пряма паралельна — пряма паралельна  3)  — пряма належить осі — пряма належить осі  4)  — пряма паралельна Ох — пряма паралельна Ох 5)  — пряма належить осі Ох — пряма належить осі Ох  . .
Т. Для того, щоб (1) і (2) співпадали Н. і Д., щоб коеф. в р-нях були пропорційні.  . .
Нехай  належить прямим, тоді має місце належить прямим, тоді має місце  (3), (3),  (4). З (3) і (4) (4). З (3) і (4)   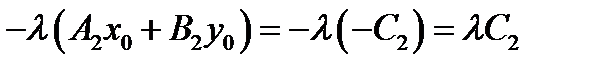 . Отже, якщо р-нями (1) і (2) задана одна і та ж пряма, то коеф. в цих р-нях пропорційні. . Отже, якщо р-нями (1) і (2) задана одна і та ж пряма, то коеф. в цих р-нях пропорційні.   — умова паралельності двох прямих. — умова паралельності двох прямих.
 — р-ня прямої, що проходить через дві точки. — р-ня прямої, що проходить через дві точки.
d не парал. до j, тому  . .  парал до парал до   (1) (1)   або або  . .  . .  — величина напрямленого кута між додатнім напрямком осі абсцис і — величина напрямленого кута між додатнім напрямком осі абсцис і  . .
     ; ;  . .  — нормальне р-ня прямої — нормальне р-ня прямої  .(2) .(2)
 (3) (3)
Оскільки (2) і (3) — одна і та ж пряма, то  . .  , ,  . . Знак  протил. до знака вільного члена в (2). протил. до знака вільного члена в (2). О. Під відстанню від т. до прямої будемо розуміти довжину  опущеного з цієї т. на пряму. опущеного з цієї т. на пряму. О. Відхиленням т.  від прямої від прямої  будемо наз. число будемо наз. число  (відстань від т. до прямої), якщо т. (відстань від т. до прямої), якщо т.  і т. і т.  знаходяться по один бік від знаходяться по один бік від  . . Т. Якщо т.  має коорд. має коорд. 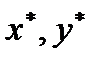 , а пряма задана нормальним р-ням , а пряма задана нормальним р-ням  , то відхилення т. , то відхилення т.  від цієї прямої задається: від цієї прямої задається:  . .  — параметричне р-ня прямої. — параметричне р-ня прямої. О. Під кутом між прямими розуміють менший з двох кутів, які утворюють ці прямі. Пучок прямих можна подати в такий спосіб:  . .
| 
 базис
базис  простору. Ця четвірка наз афінною сис координат в 3-вимірному просторі
простору. Ця четвірка наз афінною сис координат в 3-вимірному просторі  . (1)
. (1) 


 і
і  ненульові вектори. Якщо розмістити ці вектори на прямих паралельних до кожного з них і задати напрямок, що співпадає з напрямком векторів, то отримаєм дві напрямлені прямі, які в загальному випадку не перетнуться.
ненульові вектори. Якщо розмістити ці вектори на прямих паралельних до кожного з них і задати напрямок, що співпадає з напрямком векторів, то отримаєм дві напрямлені прямі, які в загальному випадку не перетнуться.
 .
. будемо називати скалярним добутком векторів
будемо називати скалярним добутком векторів  , якщо воно
, якщо воно 
 Т. Скалярний добуток двох векторів, заданих своїми координатами відносно ортонормованої бази = сумі добутків відповідних координат цих векторів:
Т. Скалярний добуток двох векторів, заданих своїми координатами відносно ортонормованої бази = сумі добутків відповідних координат цих векторів:  (1).
(1). – не колінеарні і не нульові. Виберемо точку О і відкладемо вектори
– не колінеарні і не нульові. Виберемо точку О і відкладемо вектори  . За теоремою косинусів:
. За теоремою косинусів:

 (2)
(2)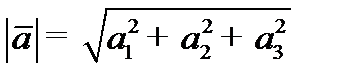 ;
;  ,
,  , тоді
, тоді  . Підставимо одержані рез-ти в (2), маємо:
. Підставимо одержані рез-ти в (2), маємо: 

 . Теорему доведено.
. Теорему доведено. і дов векторів
і дов векторів  мають місце співвідношення:
мають місце співвідношення: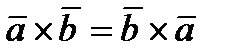 — комутативність
— комутативність — сполучна
— сполучна  — розподільна
— розподільна



 на
на  називається вектор
називається вектор  , такий що задовільняє умовам:
, такий що задовільняє умовам:
 і
і  ;
; утворюють праву трійку. Позначабть век доб
утворюють праву трійку. Позначабть век доб  .
. і
і  - колінеарні. Можливі випадки:
- колінеарні. Можливі випадки: 
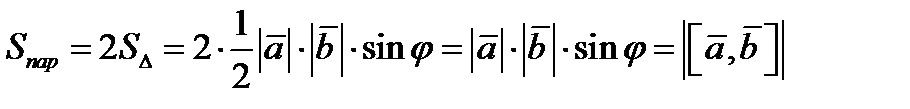
 .
. =
=  .
.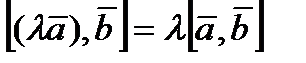 ,
,  .
.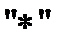 відносно
відносно 
 Т. Якщо
Т. Якщо  то відносно базису
то відносно базису 
 =
= 



 : у фізиці — механічна робота, магнітний потік.
: у фізиці — механічна робота, магнітний потік.  : момент сили, тангенціальна та кутова поверхні.
: момент сили, тангенціальна та кутова поверхні.

 .
. в ортонормованому базисі, то їх мішаний добуток = визначнику 3-го порядку, рядками якого є координати цих векторів.
в ортонормованому базисі, то їх мішаний добуток = визначнику 3-го порядку, рядками якого є координати цих векторів.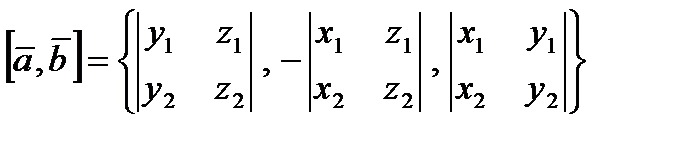 .
. 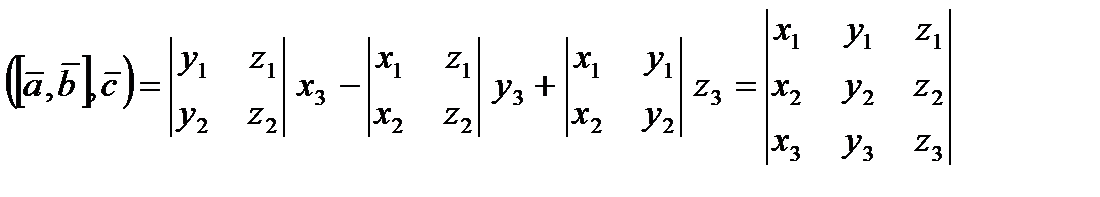
 , якщо трійка
, якщо трійка 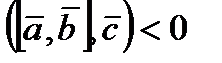 , якщо трійка
, якщо трійка  координатні вектори. Напрямлені прямі, що проходять через початок координат і паралельні коорд векторам, на яких додатній напрям визначається цими векторами, наз коорд осями. Це осі абсцис, ординат і аплікат
координатні вектори. Напрямлені прямі, що проходять через початок координат і паралельні коорд векторам, на яких додатній напрям визначається цими векторами, наз коорд осями. Це осі абсцис, ординат і аплікат  . Площини, що визначаються поч коорд і осями
. Площини, що визначаються поч коорд і осями  наз координатними площинами і позначаються
наз координатними площинами і позначаються  .
. т простору. Вектор
т простору. Вектор  — радіус-вектор т М відносно О. Координати
— радіус-вектор т М відносно О. Координати  в-ра
в-ра  – абсциса,
– абсциса, 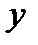 – ордината,
– ордината,  – апліката. Пишуть т
– апліката. Пишуть т  :
:  . Для побудови т
. Для побудови т  за її коорд користуються формулою:
за її коорд користуються формулою:  , від точки
, від точки  відладають век
відладають век  і від точки
і від точки  —
—  . За правилами многокутника:
. За правилами многокутника:  . М — шукана точка.
. М — шукана точка. наз коорд ламаною. Якщо виконується рівність:
наз коорд ламаною. Якщо виконується рівність:  . Век
. Век 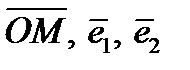 лінійно залежні, тому колінеарні. Це означає, що т
лінійно залежні, тому колінеарні. Це означає, що т  .
. , то
, то 
 що
що  т осі абсцис
т осі абсцис  .
.  .
.  .
.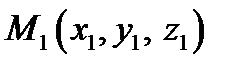 і
і  , то
, то  :
:  , де
, де  — точка, що ділить відрізок
— точка, що ділить відрізок  у відношенні
у відношенні  .
.  .
. Сис коорд наз прямокутною декартовою або декартовою, якщо базис цієї сис є ортонормованим. Таку сис коорд з початком в т О позначають так:
Сис коорд наз прямокутною декартовою або декартовою, якщо базис цієї сис є ортонормованим. Таку сис коорд з початком в т О позначають так:  або
або  , де
, де  .
.  . Нехай в прямокутній сис коорд
. Нехай в прямокутній сис коорд  і
і  , які мають координати
, які мають координати 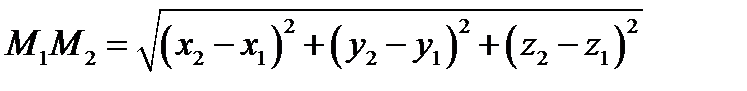
 :
:  Розглянемо в просторі дві афінні сис коорд
Розглянемо в просторі дві афінні сис коорд  . Нехай
. Нехай  т простору: в старій сис
т простору: в старій сис  . Завдання полягає в тому щоб, знаючи
. Завдання полягає в тому щоб, знаючи  ,
,  ,
,  ,
,  (1) в старій сис виразити координати
(1) в старій сис виразити координати  т М через
т М через  тієї ж точки М в новій системі. За озн. коорд. в-рів з (1):
тієї ж точки М в новій системі. За озн. коорд. в-рів з (1):  . За правилом трикутника:
. За правилом трикутника:  ,
,  ,
,  ,
,  ; (2)
; (2)
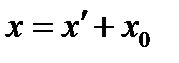 ,
,  ,
,  - ф-ли парал. перенесення.
- ф-ли парал. перенесення. ,
,  ,
,  - ф-ли при повороті.
- ф-ли при повороті. до іншої
до іншої  , можна використати ф-ли (3). Матриця переходу від базису
, можна використати ф-ли (3). Матриця переходу від базису  до
до  має вигляд:
має вигляд:  .
. , сума добутків відповідних елем.
, сума добутків відповідних елем.  2-х її різних стовпців =0, така матриця наз. ортогональною.
2-х її різних стовпців =0, така матриця наз. ортогональною. виберемо довільну т. М , яка наз. біжучою т. прямої. В-ри
виберемо довільну т. М , яка наз. біжучою т. прямої. В-ри  і
і  компланарні. Їх коорд. пропорційні
компланарні. Їх коорд. пропорційні  (1)
(1) 

 — загальне рівняння прямої.
— загальне рівняння прямої. Рівняння прямої задане напрямленим вектором, яка проходить через задану точку має вигляд:
Рівняння прямої задане напрямленим вектором, яка проходить через задану точку має вигляд:  .
. .
. Д. 1)
Д. 1)  . Поч. коорд. належить цій прямій. З другого боку, якщо пряма
. Поч. коорд. належить цій прямій. З другого боку, якщо пряма 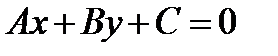 проходить через поч. коорд. тоді і т.
проходить через поч. коорд. тоді і т.  задовільняє цю рівність, а це можливо тоді коли
задовільняє цю рівність, а це можливо тоді коли  .
. — пряма паралельна
— пряма паралельна 
 — пряма належить осі
— пряма належить осі 
 — пряма паралельна Ох
— пряма паралельна Ох — пряма належить осі Ох
— пряма належить осі Ох .
. .
. належить прямим, тоді має місце
належить прямим, тоді має місце  (3),
(3),  (4). З (3) і (4)
(4). З (3) і (4) 

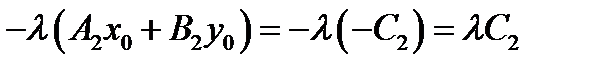 . Отже, якщо р-нями (1) і (2) задана одна і та ж пряма, то коеф. в цих р-нях пропорційні.
. Отже, якщо р-нями (1) і (2) задана одна і та ж пряма, то коеф. в цих р-нях пропорційні. 
 — умова паралельності двох прямих.
— умова паралельності двох прямих. — р-ня прямої, що проходить через дві точки.
— р-ня прямої, що проходить через дві точки. .
.  парал до
парал до  (1)
(1) 
 або
або  .
.  .
. — величина напрямленого кута між додатнім напрямком осі абсцис і
— величина напрямленого кута між додатнім напрямком осі абсцис і  .
.



 ;
;  .
.  — нормальне р-ня прямої
— нормальне р-ня прямої  .(2)
.(2) .
.  ,
,  .
. протил. до знака вільного члена в (2).
протил. до знака вільного члена в (2). опущеного з цієї т. на пряму.
опущеного з цієї т. на пряму. від прямої
від прямої  будемо наз. число
будемо наз. число  (відстань від т. до прямої), якщо т.
(відстань від т. до прямої), якщо т.  і т.
і т.  знаходяться по один бік від
знаходяться по один бік від  має коорд.
має коорд. 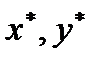 , а пряма задана нормальним р-ням
, а пряма задана нормальним р-ням  .
.  — параметричне р-ня прямої.
— параметричне р-ня прямої. .
.