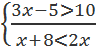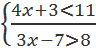ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Конъюнкция и дизъюнкция высказывательных форм

1 23

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х) Ù В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности высказывательных форм А(х) и В (х). Другими словами, при каких значениях х из области определения Х высказывательная форма А(х)ÙВ(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить Т_А – множество истинности предложения А(х), Т_В – множество истинности предложения В(х), а множество истинности их конъюнкции Т_А˄В, то, по всей видимости, Т_А˄В = Т_А Т_В.

Докажем это равенство.

1. Пусть а - произвольный элемент множества Х и известно, что а ∈ Т_А˄В. По определению множества истинности это означает, что высказывательная форма А(х)˄В(х) обращается в истинное высказывание при х = а, т.е. высказывание А(х)˄В(х) истинно. Так как данное высказывание конъюнкция, то, по определению конъюнкции, получаем, что каждое из высказываний А(а) и В(а) также истинно. Это означает, что а ∈Т_А и а ∈ Т_В. Следовательно, по определению пересечения множеств, а ∈ Т_А Т_В. Таким образом, мы показали, что Т_А˄В∈Т_А Т_В.

2. Докажем обратное утверждение. Пусть а – произвольный элемент множества Х и известно, что а ∈ Т_А Т_В. По определению пересечения множеств это означает, что а ∈ Т_А и а ∈ Т_В, откуда получаем, что А(х) и В(х) – истинные высказывания, поэтому конъюнкция высказываний А(х)˄В(х) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)˄В(х), т.е. а ∈ Т_А˄В. Таким образом, мы доказали, что Т_А Т_В ∈ Т_А˄В.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства Т_А˄В = Т_А Т_В, что и требовалось доказать.

Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.

Приведем примериспользования этого правила. Найдем множество истинности конъюнкции двух неравенств 2х > 10 и 4+х<12, т.е. множество истинности предложения 2х >10 ˄ 4+х<12. Пусть Т₁ – множество решений неравенства 2х > 10, а Т₂ – множество решений неравенства 4+х<12. Тогда Т₁= (5,+∞), Т₂ = (-∞, 8). Чтобы найти те значения х, при которых истинны оба неравенства, надо найти пересечение их множеств решений: Т₁ Т₂ = (5,8).

Видим, что выполнение этого задания свелось к решению системы неравенств.Вообще с точки зрения логики любая система неравенств есть конъюнкция неравенств, так же как и система уравнений есть конъюнкция уравнений.

Дизъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х)˄В(х). Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области определения Х, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм, т.е. Т_А˄В = Т_А Т_В.

Доказательство этого равенства проводится аналогично рассмотренному выше.

Приведем пример использования этого правила. Решим, например, уравнение (х-2)×(х+5) = 0. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Это означает, что данное уравнение равносильно дизъюнкции: х-2=0 ˄ х+5=0 и поэтому множество его решений может быть найдено как объединение множеств решений первого и второго уравнений, т.е. {2} {5}={-5; 2}.

Заметим, что дизъюнкцию уравнений (неравенств) называют также совокупностью. Решить совокупность уравнений (неравенств) – это значит найти те значения переменных, при которых истинно хотя бы одно из уравнений (неравенств), входящих в нее.

Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.

С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характеристических свойств данных множеств:

А B = {х½х∈A ˄ х∈B}, А B = {х½х∈A ˄ х∈B}, причем каждое свойство представляет собой высказывательную форму.

Упражнения

1. Покажите, что, выполняя следующие задания, мы находим множество истинности конъюнкции и дизъюнкции высказывательных форм:

а) Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30.

Выпишите все числа, в записи которых:

1) три цифры и есть цифра 3;

2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите те числа, которые:

1) двузначные или меньше 17;

2) двузначные и меньше 17.

в) Из ряда 72,312,522,483,1137 выпишите те числа, которые:

1) делятся на 3 и 9;

2) делятся на 3 или на 9.

2. Выполните следующие задания и дайте обоснование предложенным ответам:

а) Постройте по два треугольника, принадлежащих множеству А, если оно состоит из:

1) прямоугольных и равнобедренных треугольников;

2) прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых:

1) диагонали равны и есть прямой угол;

2) диагонали равны или есть прямой угол.

в) Запишите три числа, которые:

1) делятся на 4 и больше 12;

2) делятся на 4 или 12.

3. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

а)

б)

4. Решите уравнение (х-3)×(х+2) ×(х-7)=0, х ∈ R. Использовалось ли вами понятие дизъюнкции высказывательных форм?

5. Вместо многоточия вставьте «и» либо «или»:

а) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

б) х ∈ A B тогда и только тогда, когда х ∈ A …х ∈ В.

6. Пусть А – множество ромбов, В – множество прямоугольников. Как называется четырехугольник, являющийся одновременно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В?

1 23