 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Геометрическое решение задачи
В системе координат Х1ОХ2 строим график линейной зависимости, полученной переходом от неравенств к равенствам:
(1)
(2)
(3)
Пересечение этих полуплоскостей являются прямоугольник решения задачи. OABC-прямоугольник решения Построим направляющий вектор Построим начальную прямую F=0,
Для определения max целевой функции двигаем начальную прямую в направлении вектора Найдем координаты т.C. В ней пересекаются линии (1), (3) решим систему уравнения
Таким образом, С(115; 175,5). F max=F(115;175,5)= Вывод: В продукции первого вида должно быть произведено 115 едениц,второго вида 175,5. Максимальная выручка от реализации продукции составит 1973 ден.ед. Задача 2
Найдите точки экстремума заданной функции
Решение: 1) Ищем частные производные:
2)Для нахождения стационарных точек функции составим и решим систему
В нашем случае система имеет вид
3)
a)
б)
A= -14<0
Z max(-4;-1)
Задача 3 Для заданного графа произвольно пронумеровать вершины и построить кратчайшее остовное дерево, определить его длину.
Решение: Для построения кратчайшего остовного дерева воспользуемся алгоритмом Крускала. В этом алгоритме мы начинаем с пустого дерева и добавляем к нему ребра в порядке возрастания их весов пока не получим набор ребер, объединяющий все вершины графа. Если ребра закончатся до того, как все вершины будут соединены между собой, то это означает, что исходный граф был несвязным, и полученный нами результат представляет собой объединение МОД всех его компонент связности. Начнем с ребер наименьшего веса, равного 1, то есть с ребер, DL. Следующими добавляем ребро веса 2 – CG;добавляем ребра веса =4,т.е BD,BC,CK;добавляем ребра веса =5,т.е KN. Ребро CD не добавляем т. к это приводит к циклу. Добавляем ребро веса=7, т. е EL,MN,ребро DK добавлять не будем, т.к это приводит к циклу. Добавляем ребро =8 т. е AB. Добавление остальных ребер приведет к появлению цикла в уже построенной части МОД. Таким образом, кратчайшее остовное дерево для заданного графа имеет вид:
Длина построенного кратчайшего остовного дерева равна 38. Задача 4
Системасостоит из двух блоков, соединенных последовательно. Первый блок содержит три элемента: А, В, С, а второй- два элемента: D, E. Элементы каждого блока соединены параллельно. а) Найти методом Монте-Карло оценку Р* надежности системы, зная вероятности безотказной работы элементов: Р(А)=p1; Р(В)=р2; Р(С)=р3; Р(D)=р4; P(E)=р5; б) найти абсолютную погрешность êР-Р*ê, где Р- надежность системы, вычисленная аналитически. Произвести 50 испытаний. p1=0,6; p2=0,7; p3=0,4;p4=0,6; p5=0,3. Решение:
а) Выбираем из таблицы приложения (равномерно распределенные числа) пять случайных чисел: 0,10, 0,09, 0,73, 0,25 и 0,33; по правилу *) (если случайное число меньше вероятности события, то событие наступило; если случайное число больше или равно вероятности события, то событие не наступило) разыграем события А, В, С, D, E состоящие в безотказной работе соответственно элементов А, В, С. D, E. Результаты испытания будем записывать в расчетную таблицу . Поскольку Р (А)=0,6 и 0,10 <0,6, то событие наступило, т.е. элемент А в этом испытании работает безотказно. Так как Р (В)=0,7и 0,09< 0,7, то событие В наступило, т.е. элемент В работает безотказно. Так как Р(С)=0,4<0,73, то событие C не наступило, т.е. элемент С не работает. Таким образом, два элемента первого блока работают; следовательно, работает и сам первый блок. В соответствующих клетках табл. ставим знак плюс.
Таблица
Так как Р (D)=0,6 и 0,25< 0,6, то событие С наступило, т.е. элемент C работает безотказно; Р (E)=0,3 и 0,33< 0,3, то событие C не наступило, т.е. элемент С не работает; Другими словами, второй блок, а значит и вся система, Р (D)=0,6 и 0,25< 0,6, то событие С наступило, т.е. элемент C работают безотказно. В соответствующих клетках табл. ставим минус. Аналогично разыгрываются и остальные испытания. В табл. приведены результаты четырех испытаний. Произведя 50 испытаний, получим, что в 30 из них система работала безотказно. В качестве оценки искомой надежности Р примем относительную частоту Р * =30/50=0,6.
б) Найдем надежность системы Р аналитически. Вероятности безотказной работы первого и второго блоков соответственно равны:
Вероятность безотказной работы системы
Искомая абсолютная погрешность êР-Р*ê=|0,67-0,6|=0,07 Задача 5 С помощью МНК подобрать параметры a и b линейной функции Построить полученную прямую и исходные точки в одной системе координат.
Решение: Параметры
Для решения задачи составим таблицу.
Тогда система нормальных уравнений примет вид:
Решим систему. Для этого выразим
Подставим в первое уравнение:
Отсюда Итак,
Построим полученную прямую и исходные точки в одной системе координат.
Так как исходные данные и полученная прямая расположены близко друг к другу, то аппроксимирующая функция найдена правильно. Заключение
Целью данного курсовой работы была задача нахождения остова минимального веса во взвешенном графе с помощью алгоритма Краскала. Есть много способов создания модели, решающей эту задачу. Могут существовать различные алгоритмы обработки графов с разными представлениями: в виде матрицы инцидентности, матрицы смежности, матрицы весов. При решении данной задачи можно изменять вершину начала поиска остова минимального веса, при этом конфигурация остова не измениться. Она может измениться при наличии ребер одинакового минимального веса. Список используемой литература 1. Судоплатов С.В., Овчинникова Е. В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ,2002. – 208 с. 2. Кандзюба С.П., Громов В.Н. Delphi 7. Базы данных и приложения. Лекции и упражнения. – СПб: ООО «ДиаСофтЮП», 2005. – 576 с. 3. Богумирский Б. А. Энциклопедия Windows 98. 2-е изд. – СПб.: Питер, 2003–896 с. 4. Васильков Ю.В., Н.Н. Василькова «Компьютерные технологии вычислений в математическом моделировании», М. Финансы и Статистика, 1999 5. Культин Н.Б. Delphi 7 Программирование на Object Pascal. – СПб.: БХВ – Петербург, 2005. – 528 с.
|



 (1)
(1) (2)
(2) (3)
(3)



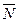 (8,6) который указывает направление возрастания целевой функции.
(8,6) который указывает направление возрастания целевой функции.

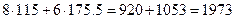
 .
.

 .
.








 - экстремума нет
- экстремума нет
 - Является точкой экстремума
- Является точкой экстремума







 , приближенно описывающей следующие опытные данные.
, приближенно описывающей следующие опытные данные.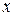

 и
и  искомой функции найдем из системы нормальных уравнений. Для этого перепишем ее в следующем виде:
искомой функции найдем из системы нормальных уравнений. Для этого перепишем ее в следующем виде:


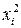

 .
.




 .
. ,
,  , и, следовательно, искомая функция имеет вид:
, и, следовательно, искомая функция имеет вид: 
 .
.