ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Контрольная задача моделирования

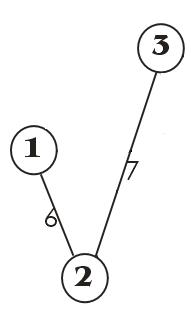
Задача . Дан взвешенный связный неориентированный граф, состоящий из пяти вершин. Необходимо найти остов минимального веса с помощью алгоритма Краскала.

Рисунок 1. Исходный граф.

Выбираем вершину начала построения остова минимального веса, напри­мер, первую вершину.

Шаг 1. Найдено ребро минимального веса: 1-2=6. Полученный остов на рисунок 2.

Рисунок 2. Полученный оостов на шаге 1

Шаг 2. Найдено ребро минимального веса: 2-3=7. Полученный остов на рисунок 3.

Рисунок 3.Полученный остов на шаге 2

Шаг 3. Найдено ребро минимального веса: 3-4=9. Полученный остов на рисунок 4.

Рисунок 4.Полученный остов на шаге 3

Шаг 4. Найдено ребро минимального веса: 3-5=11.

Рассмотрены все вершины и инцидентные ребра этим вершинам, остав­шиеся образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи.

На четвертом шаге получили окончательный остов минимального веса, ко­торый представлен на рисунке 5.

Рисунок 5. Остов минимального веса

При изменении вершины начала построения конфигурация остова мини­мального веса не измениться, а измениться лишь последовательность построения ребер остова.

Например, если в качестве начальной вершины выбрать четвертую вер­шину, то последовательность этапов построения остова минимального веса будет выглядеть следующим образом:

Шаг 1. 4-3=9;

Шаг 2. 3-2=7;

Шаг 3. 2-1=6;

Шаг 4. 3-5=11;

При этом конфигурация остова останется прежней.

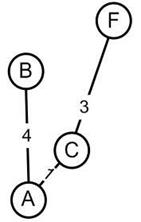
Задача №2: Дан взвешенный, связный, неориентированный граф, состоя­щий из девяти вершин. Необходимо найти остов минимального веса с помощью ал­горитма Краскала. Исходный граф на рисунке 6.

Рисунок 6. Исходный граф

Выбираем вершину начала построения остова минимального веса, напри­мер, первую вершину.

Шаг 1. Найдено ребро минимального веса: AC=1. Полученный остов на рисунок 7.

Рисунок 7. Полученный остов на шаге 1

Шаг 2. Найдено ребро минимального веса: CF=3, AB=4, AC=4. Полученный остов на рисунок 8.

Рисунок 8. Полученный остов на шаге 2

Шаг 3. Найдено ребро минимального веса: FD=4, EK=3, AE=4. Полученный остов на рисунок 9.

Рисунок 9. Полученный остов на шаге 3

Шаг 4. Найдено ребро минимального веса: KH=5, KG=4. Рассмотрены все вершины и инцидентные ребра этим вершинам, остав­шиеся ребра образуют цикл в полученном минимальном остове. А это не удовлетворяет условиям поставленной задачи.

На четвертом шаге получен окончательный остов минимального веса, ко­торый представлен на рисунке 10.

Рисунок 10. Остов минимального веса

Решим данную задачу с помощью программной модели. Чтобы решить данную задачу необходимо по­строить матрицу весов.

Таблица 1. Матрица весов

II Практическая часть

Задача 1

1) а1=0,6, а2=0,7, а3=0,6

2) В1=[700*0,6+400]=820

В2=[800*0,7+300]=860

В3=[600*0,6+300]=660

Цена единицы продукции первого вида равна 8 ден.ед., а второго вида – 6ден.ед.

Сколько единиц продукции каждого вида необходимо произвести в сутки, чтобы выручка от реализации готовой продукции была максимальной?

Решение:

Математическая модель задачи:

Решим задачу геометрическим методом.

Составим математическую модель задачи:

Пусть х₁ – количество продукции первого вида, производимой в сутки;

х₂ – количество продукции второго вида, производимой в сутки.

Найти значение х₁, х₂, дающие максимум целевой функции

При ограничениях: