 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Взаимное расположение прямой и плоскости
Точка пересечения прямой и плоскости: воспользовавшись параметрическими уравнениями прямой  , путем подстановки в общее уравнение плоскости , путем подстановки в общее уравнение плоскости  определяем параметр t и координаты точки, принадлежащей прямой и плоскости. определяем параметр t и координаты точки, принадлежащей прямой и плоскости. Угол между прямой и плоскостью: углом между прямой и плоскостью называют любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Если плоскость задана общим уравнением  , а прямая – каноническими уравнениями , а прямая – каноническими уравнениями  , то синус угла между прямой и плоскостью вычисляется по формуле , то синус угла между прямой и плоскостью вычисляется по формуле  . . Условия параллельности и перпендикулярности прямой и плоскости: если плоскость задана общим уравнением  , а прямая – каноническими уравнениями , а прямая – каноническими уравнениями  , то , то · условия параллельности -  ; ; · условия перпендикулярности -  . . Контрольная работа №1 1. Для данного определителя найти миноры и алгебраические дополнения элементов  , ,  . Вычислить определитель Δ: . Вычислить определитель Δ: · разложив его по элементам i-й строки; · разложив его по элементам j-го столбца. | 1.1 | 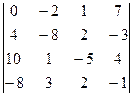 , i=4, j=2 , i=4, j=2 | 1.6 |  , i=2, j=4 , i=2, j=4 | | 1.2 |  , i=4, j=1 , i=4, j=1 | 1.7 |  , i=1, j=2 , i=1, j=2 | | 1.3 |  , i=3, j=3 , i=3, j=3 | 1.8 |  , i=2, j=3 , i=2, j=3 | | 1.4 |  , i=4, j=1 , i=4, j=1 | 1.9 |  , i=3, j=1 , i=3, j=1 | | 1.5 | 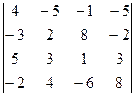 , i=1, j=3 , i=1, j=3 | 1.10 |  , i=4, j=3 , i=4, j=3 | Проверить совместность системы уравнений и в случае совместности решить ее матричным методом. | 2.1 |  | 2.6 |  | | 2.2 |  | 2.7 |  | | 2.3 |  | 2.8 |  | | 2.4 |  | 2.9 |  | | 2.5 | 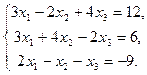 | 2.10 |  | Решить однородную систему линейных уравнений. Если система имеет бесконечное множество решений, записать ее фундаментальное решение. | 3.1 |  | 3.6 |  | | 3.2 |  | 3.7 |  | | 3.3 |  | 3.8 |  | | 3.4 |  | 3.9 |  | | 3.5 |  | 3.10 |  | 4. Показать, что векторы  образуют базис, и найти координаты вектора образуют базис, и найти координаты вектора  в этом базисе. в этом базисе. | 4.1 | 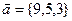 , ,  , ,  , ,  | 4.6 |  , , 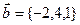 , ,  , ,  | | 4.2 |  , ,  , ,  , ,  | 4.7 |  , ,  , ,  , ,  | | 4.3 |  , ,  , ,  , ,  | 4.8 |  , ,  , ,  , ,  | | 4.4 |  , ,  , ,  , ,  | 4.9 |  , ,  , ,  , ,  | | 4.5 |  , , 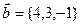 , ,  , ,  | 4.10 |  , ,  , ,  , ,  | 5. Даны векторы  , , 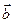 и и  . Необходимо: . Необходимо: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора. | 5.1 |  а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д) 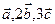 . . | 5.6 |  а) а) 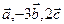 ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д) 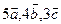 . . | | 5.2 |  а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . . | 5.7 |  а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д) 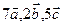 . . | | 5.3 |  а) а) 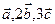 ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . . | 5.8 |  а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . . | | 5.4 |  а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . . | 5.9 |  а) а)  ; б) ; б)  ; в) ; в) 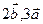 ; г) ; г)  ; д) ; д)  . . | | 5.5 |  а) а)  ; б) ; б)  ; в) ; в) 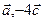 ; г) ; г)  ; д) ; д)  . . | 5.10 | 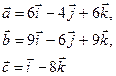 а) а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  ; д) ; д)  . . | Прямая на плоскости | 6.1 | Найти уравнение прямой, проходящей через точку пересечения прямых 3x-2y-7=0 и x+3y-6=0 и отсекающей на оси абсцисс отрезок, равный 3. | | 6.2 | Найти проекцию точки A(-8, 12) на прямую, проходящую через точки В(2, -3) и С(-5, 1). | | 6.3 | Даны две вершины треугольника АВС: А(-4, 4), В(4, -12) и точка М(4, 2) пересечения его высот. Найти вершину С. | | 6.4 | Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2у-х=3. | | 6.5 | Найти уравнение прямой, проходящей через точку А(2, -3) и точку пересечения прямых 2x-y=5 и x+y=1. | | 6.6 | Доказать, что четырехугольник ABCD – трапеция, если A(3, 6), В(5, 2), С(-1, -3), D(-5, 5). | | 6.7 | Записать уравнение прямой, проходящей через точку А(3, 1) перпендикулярно к прямой ВС, если В(2, 5), С(1, 0). | | 6.8 | Найти уравнение прямой, проходящей через точку А(-2, 1) параллельно прямой MN, если M(-3, -2), N(1, 6). | | 6.9 | Найти точку, симметричную точке М(2, -1) относительно прямой x-2y+3=0. | | 6.10 | Найти точку пересечения диагоналей четырехугольника ABCD, если A(-1, -3), В(3, 5), С(5, 2), D(3, -5). | 7. Даны четыре точки  , ,  , ,  и и  . .
Составить уравнения: а) плоскости  ; ; б) прямой  ; ; в) прямой  , перпендикулярной к плоскости , перпендикулярной к плоскости  ; ; г) прямой  , параллельной прямой , параллельной прямой  . . Вычислить: д) синус угла между прямой  и плоскостью и плоскостью  ; ; ж) косинус угла между координатной плоскостью Oxy и плоскостью  . . | 7.1 |  | 7.6 |  | | 7.2 |  | 7.7 |  | | 7.3 |  | 7.8 |  | | 7.4 |  | 7.9 |  | | 7.5 |  | 7.10 |  |
|




 , путем подстановки в общее уравнение плоскости
, путем подстановки в общее уравнение плоскости  определяем параметр t и координаты точки, принадлежащей прямой и плоскости.
определяем параметр t и координаты точки, принадлежащей прямой и плоскости. , а прямая – каноническими уравнениями
, а прямая – каноническими уравнениями  , то синус угла между прямой и плоскостью вычисляется по формуле
, то синус угла между прямой и плоскостью вычисляется по формуле  .
. ;
; .
. ,
,  . Вычислить определитель Δ:
. Вычислить определитель Δ: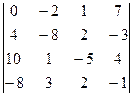 , i=4, j=2
, i=4, j=2 , i=2, j=4
, i=2, j=4 , i=4, j=1
, i=4, j=1 , i=1, j=2
, i=1, j=2 , i=3, j=3
, i=3, j=3 , i=2, j=3
, i=2, j=3 , i=4, j=1
, i=4, j=1 , i=3, j=1
, i=3, j=1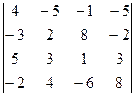 , i=1, j=3
, i=1, j=3 , i=4, j=3
, i=4, j=3






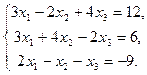











 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора  в этом базисе.
в этом базисе.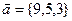 ,
,  ,
,  ,
, 
 ,
, 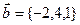 ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
, 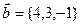 ,
,  ,
, 
 ,
,  ,
,  ,
, 
 ,
, 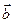 и
и  . Необходимо:
. Необходимо: а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 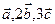 .
. а)
а) 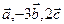 ; б)
; б)  ; в)
; в)  ; г)
; г) 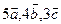 .
. а)
а)  ; б)
; б)  ; в)
; в)  ; д)
; д)  .
. а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 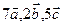 .
.  а)
а)  ; в)
; в)  ; г)
; г)  .
. а)
а)  ; б)
; б)  ; в)
; в)  .
. а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. а)
а)  ; б)
; б)  ; в)
; в) 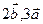 ; г)
; г)  .
. а)
а)  ; б)
; б)  ; в)
; в) 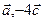 ; г)
; г)  ; д)
; д)  .
.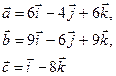 а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ,
,  ,
,  и
и  .
. ;
; ;
; , перпендикулярной к плоскости
, перпендикулярной к плоскости  , параллельной прямой
, параллельной прямой  и плоскостью
и плоскостью 








