 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Матричный метод решения систем линейных уравнений
Определители, миноры и алгебраические дополнения Определителем второго порядка квадратной матрицы второго порядка называется число Определителем третьего порядка квадратной матрицы третьего порядка называется число
Основные свойства определителей: 1. Если некоторая строка (столбец) определителя состоит из нулей, то определитель равен нулю. 2. Определитель меняет знак, если у него поменять местами две строки (два столбца). 3. Определитель, содержащий две одинаковые строки (столбца), равен нулю. 4. Величина определителя увеличивается в k раз, если элементы какого-либо столбца (строки) умножить на k. Другими словами, общий множитель можно выносить за знак определителя. 5. При транспонировании матрицы определитель не меняется. 6. Если все элементы какой-либо строки (столбца) представлены в виде суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей. 7. Если ко всем элементам какой-либо строки (столбца) прибавить умноженные на одно и то же число соответствующие элементы другой строки (столбца), величина определителя не изменится. Минором Алгебраическим дополнением элемента Определителем n-го порядка квадратной матрицы n-го порядка называется число
Пример: найти минор и алгебраическое дополнение элемента Находим:
Решение систем линейных уравнений Система линейных уравнений
Решение систем линейных уравнений по формулам Крамера
Для рассмотренной системы вычислим следующие определители:
Формулы Крамера определения решения системы линейных уравнений:
Возможны следующие ситуации: · если · если · если
Матричный метод решения систем линейных уравнений
Систему Тогда матричный метод решения системы линейных уравнений выражается следующим образом:
Алгоритм вычисления обратной матрицы: · вычислить определитель матрицы системы - · транспонировать матрицу системы; · вычислить алгебраические дополнения элементов транспонированной матрицы системы и составить из них матрицу · вычислить обратную матрицу по формуле: Пример: решить систему линейных уравнений матричным методом.
· · транспонированная матрица системы · матрица алгебраических дополнений · обратная матрица · решение системы · т.е. x = 2, y = 0, z = -1.
|



 .
.
 матрицы А n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.
матрицы А n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца. называется число, которое равняется величине минора этого элемента, умноженной на
называется число, которое равняется величине минора этого элемента, умноженной на  :
:  .
. (разложение определителя по элементам i-й строки), или
(разложение определителя по элементам i-й строки), или (разложение определителя по элементам k-го столбца).
(разложение определителя по элементам k-го столбца). и вычислить значение определителя
и вычислить значение определителя  , разложив его по элементам первой строки.
, разложив его по элементам первой строки. ,
,  ,
, .
. называется совместной, если она имеет хотя бы одно решение. Критерием совместности систем линейных уравнений служит теорема Кронекера-Капелли: для того, чтобы система была совместной, необходимо и достаточно, чтобы
называется совместной, если она имеет хотя бы одно решение. Критерием совместности систем линейных уравнений служит теорема Кронекера-Капелли: для того, чтобы система была совместной, необходимо и достаточно, чтобы  , где
, где 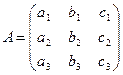 - матрица системы,
- матрица системы,  - расширенная матрица системы. Совместная система имеет либо одно решение и в этом случае называется определенной, либо у нее есть более одного решения, тогда она называется неопределенной.
- расширенная матрица системы. Совместная система имеет либо одно решение и в этом случае называется определенной, либо у нее есть более одного решения, тогда она называется неопределенной. ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
. , то система имеет единственное решение;
, то система имеет единственное решение; , но при этом либо
, но при этом либо  , либо
, либо  , либо
, либо  , то система не имеет решения;
, то система не имеет решения; и
и  и
и  , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений. , где
, где  - матрица, обратная матрице системы.
- матрица, обратная матрице системы. ;
;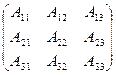 ;
;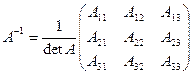 .
.
 ;
; ;
; ;
; ;
; ,
,