 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Элементы векторной алгебры
Векторы. Линейные операции над векторами. Вектором называется направленный отрезок. Координатами вектора называются его проекции на координатные оси. Вектор можно представить в виде разложения по базисным векторам декартовой прямоугольной системы координат Операции сложения (вычитания) векторов и умножения вектора на число называются линейными операциями над векторами, при этом складываются (вычитаются) или умножаются на число координаты векторов. Векторы называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Если два вектора заданы своими координатами, то условием коллинеарности векторов является пропорциональность координат, т.е. если Деление отрезка в заданном отношении. Отношением, в котором точка М(x, y) делит отрезок
Линейная зависимость векторов Векторы Пример: показать, что векторы Векторы являются линейно независимыми, если определитель, составленный из координат векторов, отличен от нуля. Вычислим определитель Скалярное произведение векторов Скалярным произведением двух векторов
Векторное произведение. Векторным произведением вектора · вектор · Векторное произведение двух ненулевых векторов равно нулю только тогда, когда эти векторы коллинеарны. Если векторы заданы своими координатами, то их векторное произведение можно вычислить по формуле
Смешанное произведение трех векторов Смешанным произведением трех векторов Если некомпланарные векторы приведены к общему началу, то модуль их смешанного произведения равен объему параллелепипеда, построенного на этих векторах. Три ненулевых вектора компланарны только тогда, когда их смешанное произведение равно нулю. Если векторы заданы координатами, то их смешанное произведение рассчитывается по формуле
Пример: даны векторы а) вычислить произведение векторов б) найти модуль векторного произведения в) вычислить скалярное произведение векторов г) проверить, будут ли коллинеарны или ортогональны векторы д) проверить, будут ли компланарны векторы
а) б) в) г) так как д) поскольку
Прямая на плоскости Общее уравнение прямой:
Уравнение прямой с угловым коэффициентом:
Уравнение прямой, проходящей через точку в данном направлении: Уравнение прямой, проходящей через две точки: Каноническое уравнение прямой: Уравнение прямой в отрезках:
Нормальное уравнение прямой:
Уравнение пучка прямых: Совокупность всех прямых плоскости, проходящих через некоторую точку, называется пучком прямых. Если точка на плоскости определена как точка пересечения прямых
Угол между прямыми: Если прямые заданы уравнениями с угловыми коэффициентами, то тангенс угла между ними можно найти по формуле Расстояние от точки до прямой: Условия параллельности двух прямых: · если прямые заданы общими уравнениями - · если прямые заданы каноническими уравнениями - · если прямые заданы уравнениями с угловыми коэффициентами - Условия перпендикулярности двух прямых:
· если прямые заданы общими уравнениями - · если прямые заданы каноническими уравнениями - · если прямые заданы уравнениями с угловыми коэффициентами - Пример: Найти прямую, проходящую через точку M(1; 1) и принадлежащую пучку
Подставим координаты точки в уравнение пучка и получим уравнение относительно λ: Плоскость Общее уравнение плоскости: Уравнение плоскости в отрезках: Уравнение плоскости, проходящей через точку в данном направлении:
Уравнение плоскости, проходящей через три точки:
Нормальное уравнение плоскости:
Уравнение пучка плоскостей: Совокупность всех плоскостей, проходящих через одну прямую в пространстве, называется пучком плоскостей. Если прямая определена как линия пересечения плоскостей
Условие параллельности плоскостей: если плоскости заданы общими уравнениями - Условие перпендикулярности плоскостей: если плоскости заданы общими уравнениями -
Прямая в пространстве Общее уравнение прямой: прямая в пространстве задается как линия пересечения двух плоскостей
Канонические уравнения прямой: Уравнения прямой, проходящей через две точки:
Параметрические уравнения прямой:
Угол между прямыми: Если прямые заданы каноническими уравнениями, то угол между прямыми вычисляется как угол между их направляющими векторами, косинус которого вычисляется по формуле
Условия параллельности двух прямых: если прямые заданы каноническими уравнениями - Условия перпендикулярности двух прямых: если прямые заданы каноническими уравнениями -
|
.
и 
- коллинеарны, то 
. Векторы называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Длина (модуль) вектора вычисляется по формуле: 
.
, называется число, удовлетворяющее равенству 
. Связь между координатами этих точек задается равенствами
, 
, 
.
называются линейно зависимыми, если существуют числа 
, не равные нулю одновременно, такие, что выполняется равенство 
. Три упорядоченных линейно независимых вектора составляют базис в пространстве. Любой вектор пространства можно разложить по базису, т.е. если векторы 
составляют базис в пространстве, то любой вектор можно представить в виде линейной комбинации базисных векторов: 
, где 
являются координатами вектора в базисе 
в этом базисе, если известно: 
, 
, 
.
. Таким образом, тройка 
и решим систему линейных уравнений 
. Решение этой систем: 
. Следовательно, 
.
и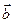 
называется число, обозначаемое 
. Если векторы заданы координатами 
. Таким образом, косинус угла между векторами можно вычислить по формуле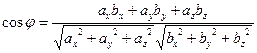 
.
, который определяется по правилу: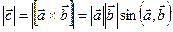
.
.
.
.
, 
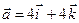и 
. Необходимо: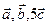
;
;
;
;
, 
;
, 
;
, 
;
, то векторы 
, то векторы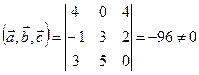 
, то векторы 
, вектор 
- нормальный вектор прямой.
, где k – тангенс угла наклона прямой к оси абсцисс.
.
.
, вектор 
- направляющий вектор прямой.
, где a и b – отрезки, отсекаемые прямой на координатных осях.
, где p – длина перпендикуляра, проведенного из начала координат к данной прямой, а α – угол, образованный этим перпендикуляром и осью абсцисс. Для приведения общего уравнения прямой к нормальному виду необходимо помножить все его члены на нормирующий множитель 
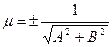, знак которого противоположен знаку свободного члена в общем уравнении прямой.
, 
, то уравнение пучка с центром в этой точке имеет вид
.
.
.
;
;
.
;
;
.
.
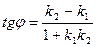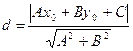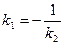. Следовательно, 
. Подставив найденное значение λ в уравнение пучка, получим уравнение искомой прямой 
.
, вектор 
- нормальный вектор плоскости.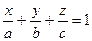
, где a, b и с – отрезки, отсекаемые плоскостью на координатных осях.
.
.
, где p –расстояние плоскости от начала координат к данной прямой, а 
– направляющие косинусы нормали. Для приведения общего уравнения прямой к нормальному виду необходимо помножить все его члены на нормирующий множитель 
, знак которого противоположен знаку свободного члена в общем уравнении прямой.
, 
, то уравнение пучка плоскостей, проходящих через эту прямую, имеет вид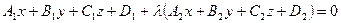
.
.
.
.
, вектор 
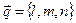- направляющий вектор прямой.
.
, где t – параметр, l, m n – координаты направляющего вектора прямой.
.
.
.