 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример 2 Интерполяционный многочлен Ньютона с разделёнными разностями
Известна зависимость
Требуется определить длину волокон, отвечающих прочности Порядок действий при решении 1) Составить программу вычисления разделённых разностей, учитывающую значения табулированной функции, номер значения функции (начинается с нуля) и порядок разделённой разности. На экране
2) Составить программу для определения значений интерполяционного многочлена Ньютона с разделёнными разностями. 3) Задать табулированную функцию в виде матрицы и ввести выражения
На экране
Ответ:прочности 150 г соответствует длина волокна хлопка 5,6 мм, а прочности 210 г – 9,4 мм.
Интерполирование сплайнами Сплайном Сплайн, для которого выполняются условия (1), называется интерполяционным. Простейшим примером сплайна является кусочно-линейная функция На практике широко применяют сплайны третьей степени
где Кубический сплайн (5) на каждом отрезке
Число уравнений системы (6) (равное Наиболее употребительными являются следующие краевые условия: 1) 2) 3) В системе Mathcad имеются следующие встроенные функции для осуществления интерполирования функции сплайнами: 1) lspline(vx,vy) – вычисляет вектор коэффициентов vs (вторых производных) линейного сплайна, построенного на векторах vx,vy; 2) pspline(vx,vy) – определяет вектор коэффициентов vs (вторых производных) параболического сплайна, построенного на векторах vx,vy; 3) сspline(vx,vy) – вычисляет вектор коэффициентов vs (вторых производных) кубического сплайна, построенного на векторах vx,vy; 4) interp(vs, vx,vy,x) – определяет значения интерполирующей функции для заданных векторов vs, vx,vy и заданного значения x. |



 между длиной
между длиной  и прочностью
и прочностью  волокон хлопка, которая приведена в таблице.
волокон хлопка, которая приведена в таблице. .
.
 ,
,  для вычисления значений в точках
для вычисления значений в точках  .
.
 называется функция, определённая на отрезке интерполирования
называется функция, определённая на отрезке интерполирования  и имеющая на нём непрерывную производную
и имеющая на нём непрерывную производную  - го порядка, которая на каждом частичном отрезке
- го порядка, которая на каждом частичном отрезке 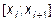 совпадает с некоторым многочленом степени не выше
совпадает с некоторым многочленом степени не выше  . При этом хотя бы на одном из частичных отрезков степень многочлена точно равна
. При этом хотя бы на одном из частичных отрезков степень многочлена точно равна  , называемая сплайном первой степени (линейным сплайном).
, называемая сплайном первой степени (линейным сплайном). (кубические сплайны). Для построения интерполяционного кубического сплайна разобьём отрезок
(кубические сплайны). Для построения интерполяционного кубического сплайна разобьём отрезок  на
на 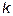 равных частичных отрезков длиной
равных частичных отрезков длиной  . В этом случае кубический сплайн на отрезке
. В этом случае кубический сплайн на отрезке  (5)
(5) - некоторые числа, причём
- некоторые числа, причём  .
. так, чтобы была непрерывна и вторая производная. Условие непрерывности второй производной в точках
так, чтобы была непрерывна и вторая производная. Условие непрерывности второй производной в точках  принимает вид системы уравнений, относительно коэффициентов
принимает вид системы уравнений, относительно коэффициентов 
 ,
,  . (6)
. (6) ). Для однозначного определения коэффициентов
). Для однозначного определения коэффициентов 
 - определяют фундаментальный кубический сплайн;
- определяют фундаментальный кубический сплайн;
 - если
- если 
 , то можно получить естественный кубический сплайн;
, то можно получить естественный кубический сплайн;
 - применяется для периодической функции с периодом
- применяется для периодической функции с периодом  .
.