 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Интерполяционный многочлен Ньютона с разделёнными разностями
ПЕНЗЕНСКАЯ ГОСУДАРСТВЕННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ
Кафедра «Прикладная математика и исследование операций в экономике»
Численные методы
Лабораторная работа №4 Интерполирование функций
Пенза, 2013 Цель работы: приобретение навыков интерполирования и экстраполирования таблично заданных функций различными численными методами Оборудование: персональный компьютер,программаMathcad. Теоретическая часть При решении многих задач приходится рассматривать функции, заданные таблично. Пусть известны значения функции
Конечное множество точек Основная задача интерполяции состоит в вычислении значений табулированной функции в неузловых точках оси
Рисунок 1 – Интерполяция функции
Задача интерполяции решается с помощью интерполяционной функции
которая удовлетворяет условиям
т.е. интерполяционная функция
Интерполяционный многочлен Лагранжа Рассмотрим полиномиальную интерполяцию, которая осуществляется при помощи многочленов, степень которых на единицу меньше числа узлов (шаг сетки может быть постоянным и непостоянным)
Чтобы найти коэффициенты
где Многочлен, коэффициенты которого определяются из системы (2), называется интерполяционным многочленом Лагранжа
Если обозначить Оценка погрешности интерполяционного многочлена Лагранжа
Рассмотрим два частных случая многочлена Лагранжа. 1) При 2) При
Пример 1 Интерполяционный многочлен Лагранжа При изучении количества предложений
Требуется определить стоимость мебели для числа предложений Порядок действий при решении 1) Задать значения узлов сетки и значения функции в виде векторов 2) Присвоить переменной 3) Ввести формулу интерполяционного многочлена Лагранжа 4) Для определения значений функции в точках На экране
5) Для построения графиков функции и интерполирующего многочлена задать пределы изменения индекса На экране
Ответ:25 предложений мягкой мебели по цене 10413,3 руб. и 43 предложения по 12050 руб. Интерполяционный многочлен Ньютона с разделёнными разностями Этот интерполяционный многочлен строится на произвольной сетке и является наиболее удобным и универсальным при решении задач интерполяции и экстраполяции. Разделённые разности первого порядка вычисляются по формуле Разделённые разности второго порядка определяются выражением
Общее выражение разделённой разности
Интерполяционный многочлен Ньютона с разделёнными разностями, удовлетворяющий условиям (1), имеет вид
Погрешность формулы (4) равна где |



 только для некоторых значений аргумента.
только для некоторых значений аргумента.



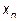





 на оси
на оси  называется сеткой, а составляющие сетку точки
называется сеткой, а составляющие сетку точки  называются узлами сетки. Расстояние между соседними узлами называется шагом сетки
называются узлами сетки. Расстояние между соседними узлами называется шагом сетки 
 . Если все шаги равны, то сетка называется равномерной, в противном случае – неравномерной.
. Если все шаги равны, то сетка называется равномерной, в противном случае – неравномерной. ; экстраполяция, если
; экстраполяция, если  ).
).
 ,
, (1)
(1) в узлах сетки
в узлах сетки  .
. интерполирующего многочлена, необходимо решить систему уравнений
интерполирующего многочлена, необходимо решить систему уравнений (2)
(2) ,
,  .
. для функции
для функции 
 , то интерполяционный многочлен Лагранжа можно записать компактным образом
, то интерполяционный многочлен Лагранжа можно записать компактным образом  (3)
(3)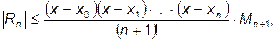 где
где  .
. - линейная интерполяция, определяемая уравнением прямой, проходящей через две заданные точки
- линейная интерполяция, определяемая уравнением прямой, проходящей через две заданные точки 
 - квадратичная интерполяция, уравнение параболы имеет вид
- квадратичная интерполяция, уравнение параболы имеет вид .
. . Построить графики функции и интерполирующего многочлена.
. Построить графики функции и интерполирующего многочлена. ,
,  .
. размерность вектора
размерность вектора  , введя выражение
, введя выражение  , затем задать пределы изменения индексов
, затем задать пределы изменения индексов  ,
,  .
. .
. , задать выражения
, задать выражения  ,
,  .
.
 и переменной
и переменной  и выполнить построение графиков.
и выполнить построение графиков.
 .
. .
. ого порядка имеет вид
ого порядка имеет вид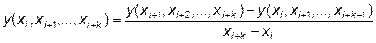 , (
, (  .
. (4)
(4)