 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Теоретические основы работы
ФОТОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ КИНЕТИКИ ГОМОГЕННЫХ РЕАКЦИЙ Лабораторная работа по курсам «Физическая химия», «Дополнительные главы физической химии» для студентов, обучающихся по программе бакалавриата по направлениям подготовки 240700 − Биотехнология 240100 − Химическая технология
Рассмотрена на заседании кафедры физической и коллоидной химии От ноября 2013 г протокол № Зав. кафедрой Марков В.Ф.
Рассмотрена на заседании методической комиссии ХТИ ноября 2013 г Протокол № Председатель методкомиссии ХТИ Миролюбов В.Р.
Екатеринбург 2014
УДК 66.092-977(075.8) ББК 35.5я73
Составитель Степановских Е.И. ФОТОМЕТРИЧЕСКОЕ ИССЛЕДОВАНИЕ КИНЕТИКИ ГОМОГЕННЫХ РЕАКЦИЙ: лабораторная работа / Екатеринбург: УрФУ, 2014. −8 с.
Рассмотрена лабораторная работа по разделу курсов «Физическая химия» и «Дополнительные главы физической химии». Описание экспериментальной части лабораторной работы соответствует изданному ранее пособию [1], однако работа существенно переработана в связи с новыми рабочими планами специальностей и использованием нового оборудования. К ней добавлено расчетное аналитическое задание.
Библиогр.: 4 назв.
© Уральский федеральный университет, 2014 Цели работы Фотометрическое исследование кинетики гомогенных реакций; решение прямой и обратной задач кинетики. Задания на лабораторную работу А. На основании экспериментальных данных определить константу скорости реакции красителя кристаллическогo фиолетового со щелочью. Б. Решить прямую и обратную кинетические задачи для реакции разложения комплексного оксалата марганца. Теоретические основы работы Интенсивность окраски щелочных растворов красителя кристаллического фиолетового убывает во времени из-за образования бесцветного продукта реакции − карбинола. Известно, что эта реакция взаимодействия кристаллического фиолетового со щелочью относится к реакциям второго порядка и является необратимой. Кинетическое уравнение реакции имеет вид
где Обычно концентрация щелочи гораздо больше, чем концентрация кристаллического фиолетового, т.е.
Реакция второго порядка становится реакцией псевдопервого порядка. Дифференциальное кинетическое уравнение такой реакции выглядит следующим образом
где (
Из анализа (4) следует, что если кинетика данной реакции действительно описывается уравнением первого порядка, то экспериментальные данные на графике зависимости логарифма текущей концентрации красителя от времени расположатся по прямой линии и по угловому коэффициенту этой линии можно найти эффективную константу скорости исследуемой реакции. А затем, если известна начальная концентрация щелочи, то и истинную константу скорости. Снятие кинетической кривой в данной работе осуществляют с использованием физико-химического метода − фотометрии. Это возможно, потому что между оптической плотностью раствора D и концентрацией красителя в некотором диапазоне концентраций
где Оптическая плотность среды по определению равна
где Учитывая, что единственным веществом, дающим окраску раствора, является кристаллический фиолетовый, уравнение (5) можно записать
и преобразовать интегральное кинетическое уравнение (4) к виду
Если на графике зависимости Рис. 1
где Из уравнения (7) видно, что |
, (1)
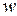- скорость реакции (здесь и далее рассматривается скорость реакций в закрытых системах постоянного объема); k - константа скорости; 
– концентрации красителя кристаллического фиолетового и щелочи в системе в разные моменты времени, так называемые «текущие» концентрации.
>> 
. В этом случае при протекании реакции концентрация щелочи в рабочем растворе практически не меняется во времени, оставаясь равной начальной ее концентрации 
. Обозначив k 
( 
. (2)
, (3)
) = 
− «текущая» концентрация красителя, а интегральная форма кинетического уравнения имеет вид
. (4)
от 0 до 1·10-2 моль/м3 существует линейная зависимость, описываемая законом Бугера−Ламберта – Бера
, (5)
– мольный показатель поглощения излучения кристаллическим фиолетовым; 
– толщина поглощающего слоя.
,
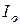и I – поверхностная плотность потока излучения (интенсивность излучения), падающего на внешнюю поверхность среды и прошедшего через среду.
, (6)
или 
. (7)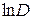
от времени (рис.1.) экспериментальные данные будут располагаться по прямой линии, то этой будет служить подтверждением указанного порядка реакции с одной 
стороны, и позволит определить эффективную константу скорости, с другой стороны.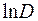
, (8)
; 
и 
; 
– координаты двух произвольно выбранных точек 
и 
на прямой, усредняющей экспериментальные данные.
. По известной концентрации щелочи в растворе можно найти истинную константу скорости: 
.