 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Средство анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа» MS Excel
Средство анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа» MS Excel служит для проверки гипотезы о равенстве дисперсий двух выборок. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.6, назначение всех полей ввода очевидно.
Рис. 4.6 Диалоговое окно средства анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа» MS Excel Результаты расчета представлены на рис.4.7. Сравните полученные результаты с результатами, полученными вручную.
Рис. 4.7 «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа» MS Excel
4.3. Критерий Стьюдента ( t-критерий) Критерий используется для проверки гипотезы о равенстве средних значений двух выборок, взятых из нормально распределенных совокупностей. Пусть заданы две генеральные совокупности x и y, имеющие нормальное распределение, из них взяты выборки Значение
где S - стандартная ошибка разности средних значений. Число степеней свободы вычисляют по формуле:
Из таблиц для заданного уровня значимости α и числа степеней свободы Если Стандартная ошибка разности средних значений S вычисляется различными способами в зависимости от поставленной задачи: · сравнение двух выборок; · сравнение двух зависимых выборок; · сравнение более двух независимых выборок. 4.3.1. Случай двух независимых выборок. Требуется сравнить средние значения двух независимых выборок. Здесь возможны два варианта: 1. Дисперсии выборок равны. 2. Дисперсии выборок не равны. Рассмотрим первый вариант (дисперсии выборок равны). В этом случае значение S вычисляется по формуле
гдеn1 и n2 - объемы первой и второй выборки; Пример 4. В двух группах учащихся — экспериментальной и контрольной — применялись две различные методики обучения: экспериментальная и традиционная. После завершения обучения был проведен тест и получены следующие результаты по учебному предмету (тестовые баллы; см. табл. 4.4). Таблица 4.4 Результаты эксперимента
Имеет ли экспериментальный метод обучения преимущество по сравнению с традиционным? Решение Для выявления преимущества экспериментального метода обучения по сравнению с традиционным можно проверить совпадения средних оценок в двух группах. Если средние отличаются незначимо, то преимущества нет, в противном случае преимущество есть. Гипотеза H0: средние значения выборок равны, альтернативная гипотеза H1 : средние значения не равны. Решение приведено на рис. 4.8-4.9. Общее количество членов выборки: n1=11, n2=9; средние значения:
Рис. 4.8. Проверка гипотезы о совпадении двух выборочных средних (фрагмент рабочего листа MS Excel в режиме отображения данных). Вычисляем значение
Вычислим табличное значение и с учетом уровня значимости α =5% (или α=0,05) получим
Рис.4.9а. Проверка гипотезы о совпадении двух выборочных средних (начало) (фрагмент рабочего листа MS Excel в режиме отображения формул)
Рис.4.9.б. Проверка гипотезы о совпадении двух выборочных средних (окончание) (фрагмент рабочего листа Excel в режиме отображения формул) |





 и
и  , т.е. n1 и n2 - объемы первой и второй выборки соответственно. Выдвигается гипотеза H0 , что средние значения выборок равны (альтернативная гипотеза H1 - средние значения не равны).
, т.е. n1 и n2 - объемы первой и второй выборки соответственно. Выдвигается гипотеза H0 , что средние значения выборок равны (альтернативная гипотеза H1 - средние значения не равны). вычисляют по формуле:
вычисляют по формуле: ,
,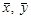 — средние арифметические выборок
— средние арифметические выборок  .
. определяют tкрит (критическое значение).
определяют tкрит (критическое значение). , то гипотеза H0 принимается, в противном случае принимается альтернативная гипотеза.
, то гипотеза H0 принимается, в противном случае принимается альтернативная гипотеза. ,
, и
и  — средние арифметические выборок.
— средние арифметические выборок. =13,636;
=13,636;  =9,444. По формуле (4.10) находим стандартную ошибку разности средних значений:
=9,444. По формуле (4.10) находим стандартную ошибку разности средних значений:


 с помощью встроенной функции СТЬЮДРАСПОБР(). Для этого определим число степеней свободы по формуле
с помощью встроенной функции СТЬЮДРАСПОБР(). Для этого определим число степеней свободы по формуле  ,
, . Так как
. Так как  , гипотеза H0 отклоняется, принимаетсягипотеза H1 . Из этого следует вывод о преимуществе экспериментального обучения.
, гипотеза H0 отклоняется, принимаетсягипотеза H1 . Из этого следует вывод о преимуществе экспериментального обучения.
