 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Экономическая интерпретация двойственной задачи
Из первой теоремы двойственности следует, что при оптимальных производственной программе и векторе оценок ресурсов производственные потери равны нулю. Согласно второй теореме двойственности в данном случае к оптимальной производственной программе если yi>0, то если если xj>0, тo если Условия (11) можно интерпретировать так: если оценка yi единицы ресурса i-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью, если же ресурс используется не полностью, то его оценка равна нулю. Из условия (12) следует, если j-й вид продукции убыточен, то он не войдёт в оптимальный план, не будет выпускаться. Аналогично продукция, которая производилась в минимально необходимом количестве (условия обращаются в равенства), получает положительную оценку yi*>0, а недефицитная продукция, которая при заданных ресурсах может быть произведена сверх необходимого количества (условия обращаются в неравенства) получает оценку yi*=0. Согласно соотношениям (11)–(12) для положительных значений неизвестных в оптимальном плане (xj>0) соответствующие сопряженные условия в системе ограничений двойственной задачи обращаются в равенства, а для нулевых значений неизвестных (xj=0), не вошедших в оптимальный план, сопряженные с ними двойственные условия, обращаются в неравенства. Из третьей теоремы двойственности следует, что величина двойственной оценки численно равна изменению целевой функции при изменении соответствующего свободного члена ограничений на единицу. DF(x)=Dbiyi, при Dbi=1 DF(x)=yi.
1.4 Пример. Планирование выпуска продукции пошивочным предприятием.
Намечается выпуск двух видов костюмов – мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Требуется определить оптимальное число костюмов каждого вида, обеспечивающее максимальную прибыль предприятия, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов и обеспечить прибыль не менее 1400 денежных единиц. Модель задачи. Введём обозначения: x1 и x2 — число соответственно женских и мужских костюмов. Прибыль от реализации женских костюмов составляет 10x1, а от реализации мужских 20x2, т.е. необходимо максимизировать целевую функцию F( Ограничения задачи имеют вид: x1³0 x2³0 x1+3,5x2£350 2x1+0,5x2£240 x1+x2£150 10x1+20x2³1400 x2³60 В соответствии с правилами составления задачи, двойственной к исходной, получим: 1. x2³60 -x2£-60 10x1+20x2³1400, -10x1-20x2£-1400. 2. 3,4. G( 5. y1+2y2+y3-10y5³10, 3.5y1+0.5y2+y3-y4-20y5³20. 6. y1,2,3,4,5 ³0.
Переменные двойственной задачи имеют следующие значения:
y1 – двойственная оценка ресурса “шерсть”, которая может быть “ценой” шерсти; y2 – двойственная оценка ресурса “лавсан”, которая может быть “ценой” лавсана; y3 – двойственная оценка ресурса “трудозатраты”, которая может быть “ценой” трудозатрат; y4 – двойственная оценка заказа мужских костюмов; y5 – двойственная оценка задания по прибыли.
x2³60 G( y1+2y2+y3-10y5³10 3.5y1+0.5y2+y3-y4-20y5³20 y1 ³0 y2 ³0 y3 ³0 y4 ³0 Y5 ³0 В результате решения задачи были получены следующие данные:
F( Таким образом, максимальная прибыль составляет 2300 денежных единиц при производстве 70 женских и 80 мужских костюмов. Шерсть и трудовые ресурсы использованы полностью; лавсана осталось 60 м; плановые задания перевыполнены по числу костюмов и по прибыли. Решение двойственной задачи указывает на дефицитность ресурсов «шерсть» (y1=4) и «трудозатраты» (y3=6). В заключение необходимо сделать важное замечание. В примере мы выяснили экономическое содержание двойственных оценок применительно к условиям примера. Что касается других типов задач линейного программирования, то интерпретация их двойственных оценок может отличаться от приведенной выше. Иногда она настолько неочевидна, что представляет серьезную проблему, особенно в задачах, в которых ограничения имеют различные знаки (£, =, ³) при неотрицательности правых частей.
Excel. Поиск решений
Excel позволяет решать сложные задачи со многими неизвестными и ограничениями. Для этого применяется математический метод линейной оптимизации. Поиск решений можно запустить, выбрав команду меню Сервис/Поиск решения. Если этого пункта в меню нет, то его следует загрузить, выполнив команду меню Сервис/Дополнения. В открывшемся диалоге следует поставить флажок Поиск решений. По команде меню Сервис/Поиск решений откроется диалог Поиск решений. В поле Установить целевую ячейку задается адрес ячейки, значение которой необходимо оптимизировать. С помощью опций в левой части диалога можно задать условие нахождения соответственно максимума, минимума или определенного ее значения. В поле Изменяя ячейки задаются адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В списке Ограничения указываются дополнительные условия, которые необходимо учитывать при поиске решения. Например, число является целым и положительным. Для того, чтобы задать новое ограничение, следует щелкнуть на кнопке Добавить. Кнопка Удалить удаляет ограничение из списка, а кнопка Редактировать дает возможность вносить изменения в параметры условия. Поиск решения начинается щелчком на кнопке Выполнить. Когда Excel находит решение, он открывает диалог. Теперь можно изменить значения ячеек в соответствии с найденным решением или восстановить предыдущие значения. В списке Тип отчета можно задать вид и объем выводимой в отчет информации по процессу нахождения решения.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Перед тем, как приступить к работе, следует ознакомиться с методическими указаниями и получить у преподавателя исходные данные (задания ида сырья S1, S2, S3. Объемы выделенного сырья, нормы расходов сырья и прибыль, полученная в результате выпуска каждого вида продукции приведены в таблице 1.
Таблица 1
Требуется найти оптимальное сочетание ресурсов, при котором прибыль максимальна.
Задание 2. Размещение производственных заказов. В планируемом периоде необходимо обеспечить производство 300 тыс. однородных новых изделий, которые могут выпускаться на четырёх филиалах предприятия. Для освоения этого нового вида изделия нужны определённые капитальные вложения. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами удельных капиталовложений и себестоимостью единицы продукции в соответствии с табл. 2. Себестоимость производства и удельные капиталовложения для каждого из филиалов условно приняты постоянными, т.е. потребность в капитальных вложениях и общие издержки будут изменяться пропорционально изменению объёмов производства изделий. Предположим, что на все филиалы предприятие для освоения 300 тыс. новых изделий может выделить 18 млн. руб. Необходимо найти такой вариант распределения объёмов производства продукции и капитальных вложений по филиалам, при котором суммарная стоимость изделий будет минимальной.
Таблица 2
Задание 3. Исходя из специализации и своих технологических возможностей предприятие может выпускать четыре вида продукции. Сбыт любого количества обеспечен. Для изготовления этой продукции используются трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объем ресурсов (в расчете на трудовую неделю), расход каждого ресурса на единицу выпускаемой продукции и прибыль, полученная за единицу продукции, приведены в табл. 3. Требуется определить план выпуска, доставляющий предприятию максимум прибыли.
Таблица 3
Задание 4. На основании информации, приведённой в табл.4, составить план производства, максимизирующий объём прибыли.
Таблица 4
Задание 5.Фабрика выпускает три вида тканей, причем суточное плановое задание составляет: не менее 90 м ткани 1 вида, 70 м — 2-го вида и 60 м — 3-го вида. Суточные ресурсы следующие: 780 единиц производственного оборудования, 850 единиц сырья и 790 единиц электроэнергии, расход которых на 1 м ткани представлен в табл. 5. Цена 1 м ткани 1-го вида равна 80 денежным единицам, 2-го вида — 70 денежным единицам, 3-го вида — 60 денежным единицам. Необходимо определить, сколько метров тканей каждого вида следует выпустить, чтобы общая стоимость выпускаемой продукции была максимальной.
Таблица 5
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать исходные данные, математические модели, результаты решения прямой и двойственной задач на ЭВМ, экономическую интерпретацию полученных результатов.
ЛИТЕРАТУРА
1. Краев В.Н., Николенко А.В. Методические указания к лабораторным работам по дисциплине "Экономико-математические методы и модели"– Владимир, ВПИ, 1993. 2. Горчаков А.А., Орлова И.В. Компьютерные экономико-математические модели: Учеб. пособие для вузов. – М.: Компьютер, ЮНИТИ, 1995. – 136 с. 3. Кузнецов А.В. и др. Высшая математика: Мат. программир.: Учеб./ А.В. Кузнецов, В.А. Сакович, Н.И. Холод, Под общ. ред. А.В. Кузнецова. – Мн.: Выш. шк., 1994 – 286 с.
|



 =(x1,x2,...,xn) и оптимальному вектору оценок
=(x1,x2,...,xn) и оптимальному вектору оценок  =(y1,y2,...,ym) предъявляются следующие требования:
=(y1,y2,...,ym) предъявляются следующие требования: i=1,...,m; (11)
i=1,...,m; (11) то yi=0, i=1,...,m;
то yi=0, i=1,...,m; j=1,...,n; (12)
j=1,...,n; (12)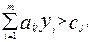 то xj=0, j=1,...,n.
то xj=0, j=1,...,n.
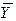 )=350y1+240y2+150y3-60y4-1400y5®min
)=350y1+240y2+150y3-60y4-1400y5®min =(70;80)
=(70;80)