 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Частотные критерии устойчивости. Критерий Найквиста
Частотные критерии устойчивости позволяют судить об устойчивости систем автоматического управления по виду их частотных характеристик. Эти критерии позволяют исследовать устойчивость систем высокого порядка и имеют простую геометрическую интерпретацию. Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду АФХ разомкнутой системы. Пусть передаточная функция разомкнутой системы имеет вид
Передаточная функция замкнутой системы по каналу управления:
Характеристическое уравнение разомкнутой системы (n-гопорядка) определено, как A(s) =0. Характеристическое уравнение замкнутой системы (n-гопорядка) выражается, как A(s)+B(s)=0. Рассмотрим, что представляет собой выражение 1 + W(s)
где Dзамк(s), Dразом(s) – характеристические полиномы, соответственно, замкнутой и разомкнутой системы. Заменяя в передаточной функции разомкнутой системы (5.1) s → iω,
получим АФХ разомкнутой системы (рис. 5.1).
Рис. 5.1. АФХ разомкнутой системы Вектор (1+W(iω)),следовательно, содержит свойства замкнутой и разомкнутой системы, и по тому, как ведет себя W(iω)относительно координаты (–1, i0), можно сделать вывод об устойчивости замкнутой системы. Выделим три случая состояния устойчивости системы. 1 случай – система в разомкнутом состоянии устойчива. Тогда согласно критерию устойчивости Михайлова [1] изменение аргумента характеристического полинома разомкнутой системы
Для устойчивости замкнутой системы должно выполняться
Отсюда следует, что приращение аргумента вектора H(iω) = (1+W(iω))
Выражение (5.5) означает, что для устойчивости замкнутой системы необходимо, чтобы вектор 1+W(iω),начало которого находится в точке (–1, i0), а конец скользит по АФХ разомкнутой системы, не охватывал точку (–1, i0) при изменении ω от 0 до ∞ (рис. 5.2). Таким образом, критерий Найквиста гласит: Если разомкнутая система автоматического управления устойчива, то замкнутая система автоматического управления будет устойчива, если амплитудно-фазовая характеристика разомкнутой системы не охватывает точку (–1, i0) при изменении ω от 0 до ∞.
а) б) Рис. 5.2. АФХ: а) разомкнутой системы; б) функции H(iω) 2 случай – система в разомкнутом состоянии неустойчива. Пусть в разомкнутом состоянии система неустойчива, при этом характеристическое уравнение разомкнутой системы имеет m корней в правой полуплоскости. Тогда согласно принципу аргумента [1]
Для того, чтобы система в замкнутом состоянии была устойчива, должно выполняться (5.3). В этом случае угол поворота вектора H(iω) = 1+W(iω)
Это означает, что АФХ функции H(iω) при изменении частоты от 0 до ∞ охватывает начало координат в положительном направлении m/2 раз. Число оборотов вектора H(iω) вокруг начала координат равно числу оборотов вектора АФХ разомкнутой системы W(iω) вокруг точки (–1, i0). На основании этого вытекает следующая формулировка критерия Найквиста. Если разомкнутая система автоматического управления неустойчива, то для того, чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы АФХ разомкнутой системы W(iω) при изменении частоты от 0 до ∞ охватывала точку (–1, i0) в положительном направлении m/2 раз, где m – число правых корней характеристического уравнения разомкнутой системы. На рис. 5.3 изображены в качестве примера АФХ H(iω) и АФХ разомкнутой системы, соответствующие устойчивой замкнутой системе, которая в разомкнутом состоянии неустойчива и m = 2.
a) б) Рис. 5.3.АФХ: а) H(iω); б) W(iω) при m = 2 При сложной форме W(iω) для определения числа ее оборотов вокруг точки (–1, i0) удобно применять «правило переходов», при котором переход W(iω) через вещественную ось при возрастании ω считается положительным, если он происходит сверху вниз, и отрицательным, если он происходит снизу вверх. Если W(iω)начинается или заканчивается на оси, то она совершает полперехода. Тогда критерий Найквиста можно сформулировать следующим образом. Если разомкнутая система автоматического управления неустойчива, то для того чтобы замкнутая система автоматического управления была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов АФХ разомкнутой системы W(iω) через отрезок вещественной оси (–∞, –1) при изменении частоты от 0 до ∞ была равна m/2, где m – число правых корней характеристического уравнения. 3 случай – система в разомкнутом состоянии нейтральна. В этом случае система должна содержать интегрирующие звенья, и тогда характеристическое уравнение разомкнутой системы имеет корни, равные нулю, и записывается в виде A(s) = sνA1(s) = 0, (5.6) где ν – порядок астатизма; А1(s) – полином, не имеющий корней, равных нулю. Амплитудно-фазовая характеристика разомкнутой системы
При ω = 0, W(iω) = ∞ и АФХ претерпевает разрыв, поэтому решать вопрос об устойчивости замкнутой системы трудно, так как неясно, охватывает АФХ точку (–1, i0) или нет. Чтобы сохранить формулировку критерия для устойчивых в разомкнутом состоянии систем, при построении годографа Михайлова при изменении частоты от –∞ до +∞ обходят начало координат по полуокружности бесконечно малого радиуса r. Тогда нулевые корни дадут такой же угол поворота, как левые корни, т.е. каждый из векторов повернется на угол π (рис. 5.4).
а) б) Рис. 5.4. АФХ нейтральной разомкнутой системы: а) – с астатизмом первого порядка, ν = 1; б) – с астатизмом второго порядка, ν = 2 Обходу начала координат по малой дуге reiφ соответствует передаточная функция разомкнутой системы
При r →0 радиус R →∞, а аргумент ψ меняется от При движении по полуокружности бесконечно малого радиуса в плоскости корней АФХ разомкнутой системы сама W(iω)может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол, равный νπ. При изменении ω от 0 W(iω)изменяется по дуге бесконечно большого радиуса, описывая угол от 0 до Система автоматического регулирования, нейтральная в разомкнутом состоянии, устойчива в замкнутом состоянии, если АФХ разомкнутой системы с его дополнением в бесконечности не охватывает точку (–1, i0) при изменении ω от 0 до ∞. Как видно из рис. 5.4, если разомкнутая система имеет астатизм первого порядка, то замкнутая система устойчива, так как точка (–1, i0) не охватывается, если же астатизм будет второго порядка, то замкнутая система неустойчива – точка (–1, i0) охватывается АФХ разомкнутой системы. Достоинствами критерия Найквиста являются: 1) применимость при неизвестных уравнениях некоторых звеньев разомкнутой системы; 2) возможность исследования устойчивости систем с запаздыванием. Сравнение рассмотренных критериев устойчивости позволяет сделать следующий вывод относительно их применимости. Критерий устойчивости Гурвица целесообразно применять, когда характеристическое уравнение имеет степень не выше четырех (n < 4). Критерий устойчивости Рауса дает быстрый ответ при численно заданных коэффициентах, им целесообразно пользоваться, когда n > 4. Критерий устойчивости Михайлова целесообразно применять при исследовании сложных многоконтурных систем, когда необходимо выяснить влияние изменения структуры системы и средств стабилизации на ее устойчивость. Критерий устойчивости Найквиста целесообразно применять при исследовании сложных систем. Этот критерий оказывается единственно применимым, когда часть или все характеристики отдельных элементов системы заданы экспериментально, применим при анализе систем, описываемых аналитическими функциями. Задание 5.1 Определить устойчивость разомкнутой системы с числом правых корней m = 2, АФХ которой изображена на рис. 5.5.
Рис. 5.5. АФХ разомкнутой системы при m = 2 На изображенной АФХ: число переходов – два положительных, один отрицательный, их разность равна Задание 5.2 Исследовать устойчивость замкнутой системы автоматического управления (рис. 5.6), если
Рис. 5.6.Замкнутая схема исследуемой системы В разомкнутом состоянии система автоматического регулирования устойчива. Амплитудно-фазовая характеристика разомкнутой системы
Определение устойчивости замкнутых систем с помощью критерия Найквиста требует расчета АФХ разомкнутых систем. Существенно упрощает процедуру построения АФХ (рис 5.7) пакет программного обеспечения Matlab. W1=tf(0.5,[0.2 1])% передаточная функция W1(s) W2=tf(4,[0.1 0.1 1])% передаточная функция W2(s) W=W1*W2% передаточная функция двух звеньев figure(1)% область графического изображения nyquist(W)% изображение АФХ.
Рис. 5.7. АФХ разомкнутой системы последовательно соединенных апериодического и колебательного звеньев Так как амплитудно-фазовая характеристика разомкнутой системы охватывает точку с координатами (–1, i0), то замкнутая система неустойчива. Задание 5.3 Исследовать устойчивость замкнутой системы автоматического управления (рис. 5.8), если
Рис. 5.8.Структурная схема системы автоматического регулирования В разомкнутом состоянии система автоматического регулирования устойчива. Амплитудно-фазовая характеристика разомкнутой системы
В случае, если запись передаточной функции трудно выразить в аналитическом виде, используют прикладной пакет Simulink, в котором можно изобразить рассматриваемую структурную схему системы с дополнительными элементами In и Out (рис. 5.8). Затем сохранить схему в рабочей области Matlab (по умолчанию) под выбранным именем, определить матрицы коэффициентов передаточной функции и саму передаточную функцию. После чего построить АФХ (рис. 5.9).
Рис. 5.8. Структурная схема последовательно соединенных апериодического звена и звена транспортной задержки [A,B,C,D]=linmod('model')% матрицы коэффициентов модели W1=ss(A,B,C,D)% передаточная функция w figure(1)% область графического изображения nyquist(W1)% изображение АФХ.
Рис. 5.9. АФХ разомкнутой системы последовательно соединенных апериодического звена и звена транспортной задержки Так как амплитудно-фазовая характеристика разомкнутой системы не охватывает точку с координатами (–1, i0), то замкнутая система устойчива. Контрольные вопросы: 1. Опишите особенности применения частотных критериев устойчивости. 2. Какой из частотных критериев позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой системы? 3. Определите вид характеристического уравнения замкнутой и разомкнутой системы. 4. Каким образом от передаточной функции переходят к амплитудно-фазовой характеристике? 5. Каким образом строится график амплитудно-фазовой характеристики? 6. На основе какого принципа построен критерий устойчивости Найквиста? 7. Как изменяется аргумент АФХ, если система устойчива в разомкнутом и замкнутом состоянии? Сформулируйте критерий Найквиста для этого случая. 8. Как изменяется аргумент АФХ, если система неустойчива в разомкнутом, но должна быть устойчива в замкнутом состоянии? Сформулируйте критерий Найквиста для этого случая. 9. Как изменяется аргумент АФХ, если система нейтральна в разомкнутом, но должна быть устойчива в замкнутом состоянии? Сформулируйте критерий Найквиста для этого случая. 10. Какой прием использован для построения АФХ системы, нейтральной в разомкнутом состоянии? 11. Что означает «правило переходов» для критерия Найквиста? 12. Поясните достоинства и недостатки известных вам критериев устойчивости. 13. Опишите методы построения АФХ.
Библиографический список
1. Шендалева Е.В. Основы автоматического управления: Конспект лекций. – Омск: ОмГТУ, 2010. – 80 с. 2. Сборник задач по теории автоматического регулирования и управления / Под ред. В.А. Бесекерского. 5-е изд., перераб. и доп. – М.: Наука, 1978. – 510 с. 3. Страшинин Е.Э. Основы теории автоматического управления. Часть 1. Линейные непрерывные системы управления: Учебное пособие – Екатеринбург: УГТУ, 2000. – 217 с. 4. Клавдиев А.А. Теория автоматического управления в примерах и задачах. Часть 1.Анализ линейных непрерывных систем автоматики: Учебное пособие. – СПб.: СЗТУ, 2005. 74 с.
Содержание
1. Динамические функции 3 2. Передаточные функции 7 3. Разложение сложной передаточной функции на более простые составляющие 14 4. Алгебраические критерии устойчивости 16 5. Частотные критерии устойчивости. Критерий Найквиста 23
|



 (5.1)
(5.1)
 , (5.2)
, (5.2)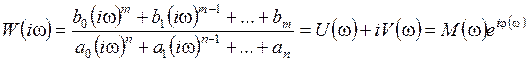 ,
,
 . (5.4)
. (5.4) (5.5)
(5.5) (5.6)
(5.6)
 .
. . (5.5)
. (5.5)
 . (5.7)
. (5.7)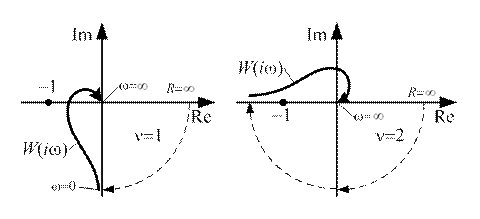
 . (5.8)
. (5.8) до
до  при изменении φ от π/2 до –π/2.
при изменении φ от π/2 до –π/2.
 , следовательно, замкнутая система устойчива.
, следовательно, замкнутая система устойчива. ;
;  .
.
 .
.
 ;
;  .
. .
.
