 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Разложение сложной передаточной функции
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Омск Издательство ОмГТУ Министерство образования и науки Российской Федерации Государственное образовательное учреждение высшего профессионального образования «Омский государственный технический университет»
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к практическим работам
Омск Издательство ОмГТУ Составитель Е. В. Шендалева, канд. техн. наук
Издание содержит методические указания к проведению практических работ по теории автоматического управления. Предназначено для студентов специальности 200503, «Стандартизация и сертификация», изучающих дисциплину «Основы автоматического управления».
Печатается по решению редакционно-издательского совета Омского государственного технического университета
© ГОУ ВПО «Омский государственный технический университет», 2011 Необходимость использования методологии теории управления для специалистов по стандартизации и сертификации возникает при определении: 1) количественных и (или) качественных характеристик свойств объекта испытаний как результата влияния на него при его функционировании, при моделировании объекта и (или) воздействий, закон изменения которых необходимо обеспечить с помощью системы автоматического управления; 2) динамических свойств объекта измерений и испытаний; 3) влияния динамических свойств средств измерений на результаты измерений и испытаний объекта. Методы исследования объектов рассмотрены в практических работах.
Практическая работа 1 Динамические функции Задание 1.1 Найти весовую функцию w(t) по известной переходной функции h(t) = 2(1–e–0,2t). Решение w(t)=h¢(t), поэтому при дифференцировании исходного выражения w(t)=0,4e–0,2t. Задание 1.2 Найти передаточную функцию системы по дифференциальному уравнению 4y¢¢(t) + 2y¢(t) + 10y(t) = 5x(t). Начальные условия – нулевые. Решение Дифференциальное уравнение преобразуют в стандартную форму делением на коэффициент при слагаемом y(t) 0,4y¢¢(t) + 0,2y¢(t) + y(t) = 0,5x(t). Полученное уравнение преобразуют по Лапласу 0,4s2y(s) + 0,2sy(s) + y(s) = 0,5x(s) и затем записывают в виде передаточной функции:
где s = a + iw – оператор Лапласа. Задание 1.3 Найти передаточную функцию W(s) системы по известной весовой функции w(t)=5–t. Решение Преобразование Лапласа
Используя связь между передаточной функцией и весовой функцией W(s) = w(s), получим
Преобразование Лапласа можно получить расчетным путем (1.1), с помощью таблиц преобразования Лапласа или с помощью пакета программного обеспечения Matlab. Программа в Matlab приведена ниже. syms s t% обозначение символьных переменных x=5-t% временная функция y=laplace(x)% функция, преобразованная по Лапласу. Задание 1.4 По передаточной функции системы найти ее реакцию на единичное ступенчатое воздействие (переходную функцию)
Решение Обратное преобразование Лапласа
где с – абсцисса сходимости x(s). По принципу суперпозиции, справедливому для линейных систем h(t)=h1(t)+h2(t), где h(t) – переходная функция всей системы; h1(t) – переходная функция интегрирующего звена
h2(t) – переходная функция усилительного звена
Известно, что h1(t)=k1×t, h2(t)=k2×δ(t), тогда h(t)= k1×t+k2×δ(t). Обратное преобразование Лапласа можно получить расчетным путем (1.2), с помощью таблиц преобразования Лапласа или с помощью пакета программного обеспечения Matlab. Программа в Matlab приведена ниже. syms s k1 k2% обозначение символьных переменных y=k1/s+k2% функция, преобразованная по Лапласу x=ilaplace(y)% временная функция. Задание 1.5 Найти амплитудно-частотную и фазочастотную характеристику по известной передаточной функции системы
Решение Для определения амплитудно-частотной (АЧХ) и фазочастотной характеристики (ФЧХ) необходимо перейти от передаточной функции к амплитудно-фазовой характеристике W(iw), для чего изменить аргумент s → iw
Затем представить АФХ в виде W(iw)=P(w)+iQ(w), где P(w) – действительная часть, Q(w) – мнимая часть АФХ. Для получения действительной и мнимой части АФХ необходимо умножить числитель и знаменатель на комплексное число, сопряженное выражению в знаменателе:
АЧХ и ФЧХ определяют соответственно по формулам
Амплитудно-фазовую характеристику W(jw) можно представить в виде
Тогда
Задание 1.6 Определить сигнал y(t) на выходе системы по известному входному сигналу и передаточной функции системы x(t)=2sin10t; Известно, что при воздействии входного сигнала x(t)=Bsinwt на систему выходной сигнал y(t) также будет гармоническим, но будет отличаться от входного амплитудой и фазой y(t) = B×A(w)sin[wt + j(w)], где A(w) – АЧХ системы; j(w) – ФЧХ системы. По передаточной функции определим АЧХ и ФЧХ
На частоте w = 10с–1 A(10) = 4/ Тогда y(t) = 2×2 Контрольные вопросы: 1. Определите понятие весовой функции. 2. Определите понятие переходной функции. 3. С какой целью используют преобразование Лапласа при описании динамических звеньев? 4. Какие уравнения называют линейными дифференциальными? 5. С какой целью при переходе к уравнению в операторном виде исходное дифференциальное уравнение преобразуют в стандартную форму? 6. Каким образом из знаменателя амплитудно-фазовой характеристики устраняют выражение с мнимым числом? 7. Укажите команду прямого преобразования Лапласа в программном пакете Matlab. 8. Укажите команду обратного преобразования Лапласа в программном пакете Matlab. Практическая работа 2 Передаточные функции Задание 2.1 Найти передаточную функцию системы по ее структурной схеме. Решение Основными способами соединения звеньев в структурных схемах являются: параллельное, последовательное и соединение звеньев с обратной связью (типовые участки звеньев). Передаточная функция системы параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев (рис. 2.1)
Рис. 2.1. Параллельное соединение звеньев Передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций отдельных звеньев (рис. 2.2)
Рис. 2.2. Последовательное соединение звеньев Обратной связью называют передачу сигнала с выхода звена на его вход, где сигнал обратной связи алгебраически суммируется с внешним сигналом (рис. 2.3).
а) б) Рис. 2.3 Соединение с обратной связью: а) положительной, б) отрицательной Передаточная функция соединения с положительной обратной связью
передаточная функция соединения с отрицательной обратной связью
Определение передаточной функции сложной системы управления производят поэтапно. Для этого выделяют участки, содержащие последовательные, параллельные соединения и соединения с обратной связью (типовые участки звеньев) (рис. 2.4) W34(s)=W3(s)+W4(s);
Рис. 2.4. Структурная схема системы управления Затем выбранный типовой участок звеньев заменяют одним звеном с рассчитанной передаточной функцией и повторяют процедуру расчета (рис. 2.5 – 2.7).
Рис. 2.5. Замена параллельного соединения и соединения с обратной связью одним звеном
Рис. 2.6. Замена соединения с обратной связью одним звеном
Рис. 2.7. Замена последовательного соединения одним звеном
Задание 2.2 Определить передаточную функцию, если передаточные функции входящих в ее состав звеньев:
Решение При подстановке в (2.5) передаточных функций звеньев
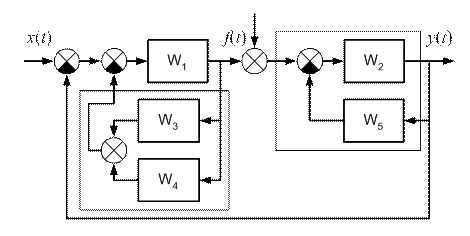
Преобразование структурной схемы относительно входного управляющего воздействия (рис. 2.7, 2.11) можно получить расчетным путем (2.5) или с помощью пакета программного обеспечения Matlab. Программа в Matlab приведена ниже. W1=tf([2],[0.1 1])% передаточная функция W1 W2=tf([0.5],[0.2 1])% передаточная функция W2 W3=tf([0.2],[1 1])% передаточная функция W3 W4=tf([2],[1 0])% передаточная функция W4 W5=tf([2 0],[0.5 1])% передаточная функция W5 W34=parallel(W3,W4)% параллельное соединение (W3 + W4) W25=feedback(W2,W5)% отрицательная обратная связь W134=feedback(W1,W34)% отрицательная обратная связь W12345=series(W134,W25)% последовательное соединение (W134×W25) W=feedback(W12345,1)% отрицательная обратная связь. Задание 2.3. Найти передаточную функцию замкнутой системы по возмущающему воздействию Решение Для того, чтобы определить передаточную функцию сложной системы по возмущающему воздействию необходимо упростить ее и рассмотреть относительно возмущающего входного воздействия (рис. 2.8 – 2.12).
Рис.2.8. Исходная структурная схема автоматической системы
Рис. 2.9. Упрощение структурной схемы
Рис. 2.10. Упрощенная структурная схема
Рис. 2.11. Структурная схема относительно входного управляющего воздействия
Рис. 2.12. Структурная схема системы относительно возмущающего воздействия После приведения структурной схемы к одноконтурной передаточная функция по возмущающему воздействию f(t)
При подстановке числовых значений
Преобразование структурной схемы относительно возмущающего воздействия (рис. 2.12) можно получить расчетным путем (2.6) или с помощью пакета программного обеспечения Matlab. W1=tf([2],[0.1 1])% передаточная функция W1 W2=tf([0.5],[0.2 1])% передаточная функция W2 W3=tf([0.2],[1 1])% передаточная функция W3 W4=tf([2],[1 0])% передаточная функция W4 W5=tf([2 0],[0.5 1])% передаточная функция W5 W34=parallel(W3,W4)% параллельное соединение W25=feedback(W2,W5)% отрицательная обратная связь W134=feedback(W1,W34)% отрицательная обратная связь Wf=feedback(W25,W134)% отрицательная обратная связь. Задание 2.4 Определить передаточную функцию замкнутой системы для ошибки. Решение Структурная схема для определения передаточной функции замкнутой системы для ошибки управления изображена на рис. 2.13.
Рис. 2.13. Структурная схема системы относительно ошибки управления
При подстановке числовых значений
Преобразование структурной схемы относительно сигнала ошибки управления (рис. 2.13) можно получить расчетным путем (2.7) или с помощью пакета программного обеспечения Matlab. W1=tf([2],[0.1 1])% передаточная функция W1 W2=tf([0.5],[0.2 1])% передаточная функция W2 W3=tf([0.2],[1 1])% передаточная функция W3 W4=tf([2],[1 0])% передаточная функция W4 W5=tf([2 0],[0.5 1])% передаточная функция W5 W34=parallel(W3,W4)% параллельное соединение) W25=feedback(W2,W5)% отрицательная обратная связь W134=feedback(W1,W34)% отрицательная обратная связь We=feedback(1,W134*W25)% отрицательная обратная связь Контрольные вопросы: 1. Перечислите основные способы соединения звеньев в структурных схемах. 2. Определите передаточную функцию системы параллельно соединенных звеньев. 3. Определите передаточную функцию системы последовательно соединенных звеньев. 4. Определите передаточную функцию с положительной обратной связью. 5. Определите передаточную функцию с отрицательной обратной связью. 6. Определите передаточную функцию линии связи. 7. C помощью какой команды Matlab определяется передаточная функция двух параллельно соединенных звеньев? 8. C помощью какой команды Matlab определяется передаточная функция двух последовательно соединенных звеньев? 9. C помощью какой команды Matlab определяется передаточная функция звена, охваченного обратной связью? 10. Изобразите структурную схему системы для определения передаточной функции по управляющему воздействию. 11. Напишите передаточную функцию по управляющему воздействию. 12. Изобразите структурную схему системы для определения передаточной функции по возмущающему параметру. 13. Напишите передаточную функцию по возмущающему параметру. 14. Изобразите структурную схему системы определения передаточной функции для ошибки управления. 15. Напишите передаточную функцию для ошибки управления. Практическая работа 3 Разложение сложной передаточной функции |



 ,
, . (1.1)
. (1.1) .
. .
. , (1.2)
, (1.2) ;
; .
. .
. .
. .
. ,
,  ;
; ,
, 
 .
.

 .
. j(w)=–arctg0,1w.
j(w)=–arctg0,1w. = 2
= 2  . (2.1)
. (2.1)
 (2.2)
(2.2)


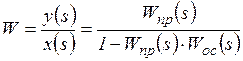 , (2.3)
, (2.3) . (2.4)
. (2.4) .
.





 (2.5)
(2.5)






 (2.6)
(2.6)

 Передаточная функция замкнутой системы для ошибки
Передаточная функция замкнутой системы для ошибки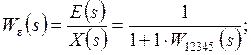
 (2.7)
(2.7)