 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Влияние параметров САУ на её устойчивость.
Федеральное Агентство Железнодорожного транспорта Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования Петербургский государственный университет путей сообщения Кафедра «Электрическая тяга» Якушев А.Я., Викулов И.П., Цаплин А.Е.
Влияние параметров САу На устойчивость и качество регулирования Методические указания к лабораторной работе
Санкт-Петербург
Цель работы - изучение основных параметров а также их соотношений, определяющих устойчивость и динамические свойства систем автоматического управления (САУ), характеризуемые видом переходных процессов изменения выходной переменной при возмущающих воздействиях. Структурная схема САУ Анализ динамических свойств системы автоматического управления обычно выполняют аналитически по структурной схеме или используя математическую модель системы. Оценку динамических свойств производят по реакции выходной переменной y(t) в виде переходной функции системына ступенчатое изменение задающего Dg×1(t) или возмущающего DZ×1(t)воздействий. Структурной называют схему, составленную из операторных передаточных функций звеньев направленного действия, образующих систему автоматического управления. Основой для составления структурной схемы служит функциональная схема САУ (рис.1, а) и динамические характеристики составляющих ее элементов. Динамические характеристики функциональных элементов в структурной схеме представлены операторными передаточными функциями (рис. 1,б). Задающее воздействие g(t), возмущающее воздействие Z(t), выходная переменная y(t) на структурной схеме представлены операторными изображениями их конечных изменений, Dg(p), DZ(p), DY(р) относительноустановившихся уровней. Изменение выходной переменной DY(р) определяется операторными передаточными функциями замкнутой системы по задающему Dg(р) ивозмущающему DZ(р) воздействиям.
Рис.1 Динамические характеристики функциональных элементов САУ в большинстве случаев могут быть представлены апериодическими звеньями 1-го порядка, а также безынерционными усилительными звеньями. Характеристики более сложных функциональных элементов могут быть представлены двумя или несколькими звеньями. В работе производится исследование переходных процессов автоматического регулирования при возмущающих воздействиях DZ=1(t) применительно к простейшей системе автоматического управления. На структурной схеме (рис. 1,б) функциональные элементы исследуемой системы: объект регулирования, исполнительное устройство, элемент обратной связи представлены апериодическими звеньями 1-го порядка. Динамические параметры функциональных элементов имеют обозначения: Тор, Тиу, Тос - постоянные времени,
Влияние параметров САУ на её устойчивость. Устойчивостью системы автоматического управления называют способность системы при воздействиях на неё возмущающих факторов приходить с течением времени к равновесному состоянию. Различают устойчивость статическую и динамическую. Статическая устойчивостьобеспечивается наличием отрицательной главной обратной связи и отсутствием местных положительных обратных связей в структурной схеме системы автоматического управления. Поэтому ее называют схемной устойчивостью. Аналитические условия обеспечения статической устойчивости определяется положительностью всех коэффициентов общего дифференциального или характеристического уравнений системы. Это условие называют необходимым условием устойчивости. Характеристическое уравнение представляет собой алгебраическое уравнение, в котором показатели степени независимой переменной соответствуют порядку производных выходной переменной общего дифференциального уравнения системы:
Коэффициенты слагаемых характеристического уравнения равны коэффициентам при производных выходной переменной общего дифференциального уравнения системы автоматического управления:
Характеристическое уравнение может быть получено из полинома знаменателя передаточной функции замкнутой системы при использовании для анализа структурной схемы САУ [1]. Для исследуемой системы автоматического управления, структурная схема которой показана на рис. 1,б, передаточная функция замкнутой системы по возмущающему воздействию DZ(р) имеет следующий вид:
В выражении (1) обозначен К0 общий коэффициент усиления, равный произведению коэффициентов усиления всех звеньев, входящих в замкнутый контур структурной схемы САУ:
Для получения характеристического уравнения системы надо приравнять нулю знаменатель передаточной функции (1):
В результате преобразования получено характеристическое уравнение системы автоматического управления, представляющее собой алгебраическое уравнение третьей степени:
Коэффициенты этого уравнения определяются следующими выражениями:
Из соотношений формул (4) видно, что все коэффициенты характеристического уравнения (3) положительны, следовательно, обеспечено необходимое условие устойчивости, т.е. исследуемая система автоматического управления статически устойчива. Для оценки динамической устойчивости разработаны способы, определяющие достаточные условия, называемые критериями устойчивости. Одним из них является алгебраический критерий Гурвица. Согласно критерию устойчивости Гурвица условие динамической устойчивости системы третьего порядка определяется соотношением коэффициентов характеристического уравнения (3) [1]:
Из соотношения (5) следует, что система будет устойчива, если общий коэффициент усиления системы
После подстановки в это неравенство выражений для коэффициентов (4) характеристического уравнения и некоторых преобразований получено соотношение для общего коэффициента усиления К0 устойчивой системы 3-го порядка:
Критическим называют общий коэффициент усиления К0кр, определяемый для системы 3-го порядка равенством (6), при котором система автоматического управления находится в граничном состоянии устойчивости. Из соотношения (6) следует, что при равенстве постоянных времени апериодических звеньев Тор=Тиу=Тос, определяется наименьшее значение критического коэффициента усиления системы 3- го порядка К0кр=8. При изменении соотношений постоянных времени критический коэффициент усиления системы возрастает, например, при Работоспособность системы автоматического управления определяется не только устойчивостью, но и приемлемым характером переходного процесса выходной переменной при возмущающих воздействиях на систему. Практически величина общего коэффициента усиления К0, при которой характер и длительность переходного процесса будут удовлетворительными, должна быть примерно в 4…5раз меньше критического значения. Значит для приведённых в примерах соотношений постоянных времени общий коэффициент усиления реальной системы с удовлетворительным переходным процессом должен быть в пределах К0=2...4. |





 ,
,  ,
,  - коэффициенты усиления. В исследуемой системе применен регулятор с пропорциональным законом регулирования, характеризуемым коэффициентом усиления
- коэффициенты усиления. В исследуемой системе применен регулятор с пропорциональным законом регулирования, характеризуемым коэффициентом усиления  . Таким образом, анализ влияния параметров системы автоматического управления на её устойчивость и форму переходного процесса изменения выходной переменной
. Таким образом, анализ влияния параметров системы автоматического управления на её устойчивость и форму переходного процесса изменения выходной переменной 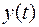 производится применительно к системе 3-го порядка, составленной из усилительного звена и апериодических звеньев 1-го порядка.
производится применительно к системе 3-го порядка, составленной из усилительного звена и апериодических звеньев 1-го порядка.
 .
.
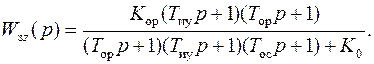 (1)
(1) . (2)
. (2)
 (3)
(3) . (4)
. (4) . (5)
. (5) , входящий в выражение коэффициента а3 характеристического уравнения системы, будет меньше величины:
, входящий в выражение коэффициента а3 характеристического уравнения системы, будет меньше величины: .
. . (6)
. (6) и
и  , К0кр=16,8.
, К0кр=16,8.