 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА
Общий вид лабораторного стенда изображен на рис.4. Фрагмент мнемонической схемы для данной работы представлен на рис.5.
Рис.4. Общий вид лабораторного стенда.
Рис.5. Фрагмент мнемонической схемы.
Аналоговое управляющее устройство (рис.5) состоит из следующих основных блоков: - задающего устройства; - устройства сравнения; - интегрирующего блока; - выходного сумматора. Задающее устройство позволяет формировать следующий сигнал задающего воздействия:
Модель объекта управления (рис.5) реализует следующая передаточная функция:
где
Постоянными времени
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Собрать схему моделирования линейной САУ (рис.5), задав параметры в соответствии с таблицей. Варианты значений параметров схемы моделирования
2. Рассчитать область возможных значений суммарного коэффициента передачи интегрирующего блока 3. Для САУ с П-регулятором рассчитать установившуюся ошибку eуст. Построить график зависимости еуст=f( где 4. Снять экспериментально зависимость еуст=f( 5. Проверить экспериментально выполнение условий устойчивости для И- и ПИ-регуляторов. 6. Раccчитать оптимальные значения суммарного коэффициента передачи интегрирующего блока 7. Определить экспериментально зависимость интегральной оценки от суммарного коэффициента передачи
8. Для САУ с И-, ПИ-регуляторами экспериментально исследовать переходной процесс. Определить величину перерегулирования и время переходного процесса при следующих значениях суммарного коэффициента передачи интегрирующего блока:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ 1. При задании суммарных коэффициентов передачи
следует учитывать, что постоянные коэффициенты имеют значения
Коэффициенты передачи потенциометров сп, и сg могут задаваться в пределах 0,05 - Т. Интегрирующий блок имеет два диапазона: ku и 10 ku, то есть позволяет получить постоянные коэффициенты передачи 1 c-1 и 10 c-1, 2. При подготовке схемы моделирования следует отключить ненужные блоки путем установки потенциометров сп, сg в положение нулевого коэффициента передачи. Тумблеры в цепях обратной связи модели объекта управления и выходного сигнала управляющего устройства следует поставить в нижнее положение, 3. Для всех экспериментов выбрать задающее воздействие g(t)= 0,5·1(t). Величину задающего воздействия следует отрегулировать соответствующим потенциометром после подачи команда "Пуск". 4. При определении времени переходного процесса переключатель секундомера установить в положение "от e ". 5. При определении квадратичной оценки могут использоваться два диапазона (J или 10J) вычислителя оценки. При выборе диапазона следует руководствоваться удобством отсчета значений и отсутствием зашкаливания измерительного прибора.
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать: 1. Структурную схему исследуемой системы автоматического управления. 2. Расчеты условий устойчивости, установившейся ошибки. 3. Графики: - теоретической и экспериментальной зависимости - экспериментальной зависимости ; - переходных процессов по пункту 8 лабораторного задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определенно статической и астатической систем. 2. Связь установившейся ошибки с передаточной функцией системы и входным сигналом. 3. Влияние параметров П-, ПИ-, И-рeгyляторов на переходный процесс системы. 4. Оценки качества переходного процесса. 5. Анализ результатов эксперимента (объяснить причину возникновения экстремума оценки). 6. Влияние типа регулятора на устойчивость и ошибку системы. 7. Понятие устойчивости процесса управления. 8. Понятие «характеристическое управление САУ». 9. Как изображаются корни характеристического уравнения на комплексной плоскости? 10. Необходимое (но не достаточное) условие устойчивости. 11. Формулировка критерия устойчивости Гурвица. 12. Алгебраический критерий устойчивости. 13. Матрица Гурвица. 14. Условия устойчивости для уравнений первого порядка. 15. Условия устойчивости для уравнений второго порядка. 16. Условия устойчивости для уравнений третьего порядка. 17. Условия нахождения системы на границе устойчивости. 18. Апериодическая граница устойчивости. 19. Колебательная граница устойчивости. 20. Частотные критерии устойчивости. 21. Принцип аргумента. 22. Формулировка критерия устойчивости Найквиста. 23. Характеристический полином замкнутой системы. 24. Необходимое и достаточное условие для устойчивости замкнутой системы. 25. Формулировка правила переходом. 26. Определение устойчивости замкнутой системы по АФХ разомкнутой. 27. Определение устойчивости замкнутой системы по логарифмическим частотным характеристикам. 28. Запас устойчивости по фазе - 29. Запас устойчивости по амплитуде - 30. Что такое частота среза - 31. Достаточные запасы устойчивости на практике
ЛИТЕРАТУРА
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПб.: Изд. «Профессия», 2004. 2. Методы классической и современной теории автоматического управления. В 5т. Учебник для вузов. Под ред. К.А.Пупкова, Н.Д.Егупова. – М.: Изд. МГТУ им.Баумана, 2004. 3. Конспект лекций.
|





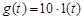 .
. ,
, - постоянный коэффициент передачи объекта управления;
- постоянный коэффициент передачи объекта управления; - коэффициент передачи потенциометра модели
- коэффициент передачи потенциометра модели  ;
; - постоянные времени.
- постоянные времени.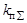




 , при которых выполняется условие устойчивости САУ· Расчет выполнить отдельно для И- и ПИ-регуляторов с учетом приведенных в таблице параметров.
, при которых выполняется условие устойчивости САУ· Расчет выполнить отдельно для И- и ПИ-регуляторов с учетом приведенных в таблице параметров. .
.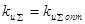 .
. .
. ;
;  .
. ;
; 
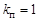 ;
; 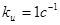 .
.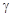 .
. .
. .
. .
.