 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Интегральная оценка качества
Интегральная оценка качества относится к аналитическим методам исследования качества системы и дает общую оценку скорости затухания и отклонения управляемой величины в совокупности, без определения данных параметров в отдельности. Простейшей интегральной квадратичной оценкой является оценка вида
где е(t)=g(t)-y(t) - ошибка системы; g(t) - задающее воздействие; y(t) - регулируемая величина. Если е(t) имеет постоянную составляющую в виде установившегося значения eуст, то интеграл J0 будет расходящимся, поэтому в качестве ошибки берут динамическую ошибку системы e1(t), т.е. отклонение регулируемой величины y(t) от ее установившегося значения:
e1(t)= yуст -y1(t)= g(t)- eуст -y(t)= e(t)- eуст .
Интегральная квадратичная оценка может быть определена по изображению ошибки:
Для практических целей более удобной является формула Релея, которая получается заменой р (10) на jω:
Если подынтегральное выражение представить в виде
где
то интеграл (10) будет вычисляться по формуле
где
Выбор оптимальных параметров управляющего устройства по минимуму интегральной оценки При заданной структуре САУ задача выбора параметров сводится к следующему. Необходимо отыскать такие значения изменяемых параметров, при которых квадратичная интегральная оценка становится минимальной. В системе автоматического управления, исследуемой в лабораторной работе, переменным параметром является постоянная времени интегратора Tu. Все постоянные времени и коэффициенты передачи заданы константами. Следовательно, задача состоит в определении оптимального значения Tu опт, при котором J0=min. В качестве управляемого устройства рассматривается И- или ПИ-регулятор. Запишем изображения ошибки Е1(р) при T1= T2 : для И-регулятора
для ПИ-регулятора
Соcтавим выражение для квадратичной интегральной оценки в виде (11) в случае ПИ-регулятора. Определим полиномы Α(jω) и B(jω) соглаcно уравнениям (12) и (13)
Из выражений (15) и (16) найдем коэффициенты аi и bi:
При подстановке данных коэффициентов в (14) получим выражение интегральной квадратичной оценки для ПИ-регулятора:
Выражение для J0 в случае И-регулятора получается из (17) как частный случай подстановкой kп= 0 для И-регулятора:
Искомое значение Tu опт при котором квадратичная оценка имеет минимум, найдем, дифференцируя (17) и (18) по Tu и приравнивая производную к нулю. Окончательно имеем для ПИ-регулятора
для И-регулятора
При схемотехнической и программной peaлизации рассмотренных регуляторов удобнее пользоваться коэффициентом передачи интегрирующего блока, который является обратной величиной по отношению к постоянной времени. В управляющей системе СУЛ-3 суммарный коэффициент передачи интегрирующего блока определяется двумя параметрами: ku и cи :
Исходя ив выражений (19) и (20), получим значение оптимального суммарного коэффициента передачи интегрирующего блока. При использовании ПИ-регулятора он равен
Для И - регулятора оптимальный коэффициент передачи интегрирующего блока составляет
|



 ,
, .
. .
.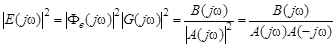
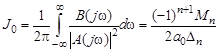
 - старший определитель Гурвица;
- старший определитель Гурвица; .
. ;
; .
. ;
; .
.

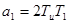





 .
. ;
; .
. .
. .
. .
.