 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ
3.1. Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:
Для сокращенной записи того, что непрерывная случайная величина Х имеет нормированный (стандартный) нормальный закон распределения с параметрами m=0и s=1, принято условное обозначение Х~N(0,1). График функции f0(х) называется нормированной нормальной кривой, кривой ошибок или просто стандартной кривой (рис.7). Функция f0(х) и стандартная кривая имеют следующие свойства: 1) Область определения функции f0(х) - вся числовая ось (-µ; +µ). 2) Функция f0(х) может принимать только положительные значения: f0(х)>0, т.е. стандартная кривая расположена над осью 0Х. 3) Ось 0Х - горизонтальная асимптота стандартной кривой. 4) Стандартная кривая симметрична относительно прямой х=0. 5) При х=m=0 стандартная кривая имеет максимум:
Рис.7. Стандартная (нормированная) кривая (график плотности распределения вероятностей случайной величины, имеющей нормированное нормальное распределение)
Рис.8. График интегральной функции распределения вероятностей случайной величины, имеющей нормированное нормальное распределение 6) При хп=m±s=±1 нормальная кривая имеет перегиб:
3.2.Интегральная функция распределения нормированной нормальной случайной величины:
График функции F0(х)приведен на рис.8. При х=0 функция F0(х)=0,5.
3.3.Числовые характеристикинормированнойнормальной случайной величины: Mатематическое ожидание, модаимедианасовпадают и равны нулю: M(X)=Мо=Ме= 0. ДисперсияD(X) =s2=1. Среднее квадратическое отклонениеs(Х)=s=1. Коэффициент ассиметрииА=0. Коэффициент эксцессаe=3, эксцесс Е=e-3=0. 3.4. Свойства нормированной нормальной случайной величины:
1) Вероятность попадания нормированной нормальной случайной величины Х в интервал (0;х) равна функции Лапласа (рис.7):
Геометрически функция Лапласа представляет собой заштрихованную площадь под стандартной кривой на отрезке (0; х).
2) Интегральная функция распределения случайной величины, имеющей нормированное нормальное распределение, выражается через функцию Лапласа по формуле: F0(х)=0,5 +Ф(х).
Геометрически (рис. 9) интегральная функция распределения представляет собой заштрихованную площадь под стандартной кривой на интервале (-µ; х). Она состоит из двух частей: первой, на интервале (-µ; 0), равной 0,5, т.е. половине всей площади под стандартной кривой, и второй, на интервале (0; х), равной функции Лапласа.
Рис. 9. Стандартная кривая с заштрихованной площадью, численно равной интегральной функции распределения F0(х) 3) Любую нормальную случайную величину можно преобразовать в нормированную: если случайная величина Х имеет нормальный закон распределения с параметрами mи s, то случайная величина ПРИМЕР 7. Доказать, что если случайная величина Х имеет нормальный закон распределения с параметрами mи s, то нормированная случайная величина Решение. Найдем математическое ожидание и дисперсию случайной величины Z:
При решении примера 7 использованы свойства математического ожидания и дисперсии, которые более подробно рассмотрены в методических указаниях [5]: 1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С. 2. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий: М(Х±У)=М(Х)±М(У). 3. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х). 4. Дисперсия постоянной величины равна нулю: D(С)=0. 5. Дисперсия суммы (разности) случайных величин равна сумме их дисперсий: D(Х±У)=D(Х)+D(У). 6. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ)=С2D(Х). |




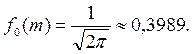









 имеет нормированное (стандартное) нормальное распределение с параметрами m=0 и s=1.
имеет нормированное (стандартное) нормальное распределение с параметрами m=0 и s=1.
