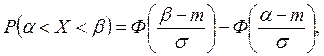ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
«МАТИ- РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ имени К.Э. ЦИОЛКОВСКОГО»
Кафедра «Моделирование систем и информационные технологии»
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Методические указания к практическим занятиям по дисциплине «Математика»
Составители: Ю.Б. Егорова И.М. Мамонов А.В. Челпанов
МОСКВА 2013
ВВЕДЕНИЕ Методические указания предназначены для студентов дневного и вечернего отделений факультета № 14 направлений подготовки бакалавров 150100.62, 160700.62, 220700.62, 230100.62. Методические указания служат основой для практических занятий и выполнения индивидуальных заданий.
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1.1.Нормальный закон распределения (закон Гаусса) наиболее часто встречается на практике. Он появляется в тех случаях, когда непрерывная случайная величина является результатом влияния большого числа факторов. Примеры случайных величин, имеющих нормальный закон распределения: ошибки измерений; отклонения при стрельбе; отклонение размеров деталей от номинальных при их изготовлении; рост, вес людей; температура воздуха, тела, объекта и т.п.
1.2. Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:
где mи s - параметры нормального распределения: m=М(Х) - математическое ожидание случайной величины Х, s=s(Х) - среднее квадратическое отклонение. Если параметры распределения известны, функция fN(х)полностью определена. Для сокращенной записи того, что непрерывная случайная величина Х имеет нормальный закон распределения с параметрами mи s, принято условное обозначение Х~N(m,s). График функции fN(х) называется нормальной кривой или кривой Гаусса (рис.1). Функция fN(х) и нормальная кривая имеют следующие свойства: 1) Область определения функции fN(х) - вся числовая ось (-µ; +µ); 2) Функция fN(х) может принимать только положительные значения: fN(х)>0, т.е. нормальная кривая расположена над осью 0x; 3) Ось 0х - горизонтальная асимптота нормальной кривой; 4) Нормальная кривая симметрична относительно прямой х=m; 5) При х=mнормальная кривая имеет максимум:
6) При хп=m±sнормальная кривая имеет перегиб:
1.3.Интегральная функция распределения вероятностей нормальной случайной величины:
График функции FN(х)приведен на рис.2.
Свойства интегральной функции распределения нормальной случайной величины: 1) Функция FN(x)есть неубывающая и непрерывная функция; 2) Функция FN(x)есть неотрицательная функция, заключенная между нулем и единицей: 0£FN(x)£1; 3) FN(-µ) =0; FN(+Ґ) = 1; 4) При х=mфункция FN(х)=0,5.
Mатематическое ожидание, модаимедианасовпадают и равны m: M(X)=Мо=Ме= m. ДисперсияD(X) =s2. Среднее квадратическое отклонениеs(Х)=s. Коэффициент ассиметрииА=0. Коэффициент эксцессаe=3, эксцесс Е=e–3=0.
1.5.Вероятность попадания в заданный интервал: вероятность того, что нормальная случайная величина Х попадет в заданный интервал (a,b), равна:
где Ф(z)- функция Лапласа. Свойства функции Лапласа приведены ниже (см. п.2).
1.6.Вероятность заданного отклонения: вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d, равна:
1.7. Правило «3s». Если случайная величина Х имеет нормальный закон распределения, то практически достоверно, что все ее значения находятся в "трех-s" интервале (m-3s, m+3s):
ПРИМЕР 1.Найти интегральную и дифференциальную функции распределения, если непрерывная случайная величина Х имеет нормальный закон распределения с параметрами: m=3, s=4. Построить нормальную кривую и график интегральной функции распределения. Найти числовые характеристики. Решение. Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:
Интегральная функция распределения:
Для построения нормальной кривой используем свойства функции fN(x)и правило «3s» : 1) Область определения функции fN(х) - вся числовая ось (-µ; +µ). 2) Так как функция fN(х) может принимать только положительные значения fN(х)>0, то нормальная кривая расположена над осью 0х. 3) Ось 0х - горизонтальная асимптота нормальной кривой. 4) Нормальная кривая симметрична относительно прямой х=m=3. 5) Приблизительно все значения х заключены в трехсигмовом интервале: [m–3s; m+3s]=[3–3×4; 3+3×4]=[-9; 15]. 6) При х=m=3 нормальная кривая имеет максимум:
7) При хп=m±s=3±4=-1;7 нормальная кривая имеет перегиб:
График функции fN(x) (нормальная кривая) представлен на рис.3. Для построения графика интегральной функции распределения используются свойства функции FN(x) и правило «3s»: 1) Функция FN(x)есть неубывающая и непрерывная функция. 2) Функция FN(x)есть неотрицательная функция, заключенная между нулем и единицей: 0£FN(x)£1. 3) FN(-µ) =0; FN(+Ґ) = 1. 4) При х=m=3 функция FN(х)=0,5. 5) Приблизительно все значения х заключены в трехсигмовом интервале: [m–3s; m+3s]=[3–3×4; 3+3×4]=[-9; 15]. График функции FN(x) приведен на рис.4. Числовые характеристики нормальной случайной величины: Mатематическое ожидание, мода и медиана: M(X)=Мо=Ме= m=3.
Дисперсия D(X) =s2=16. Среднее квадратическое отклонение s(Х)=s=4. Коэффициент ассиметрии А=0. Коэффициент эксцесса e=3, эксцесс Е=e-3=0.
|