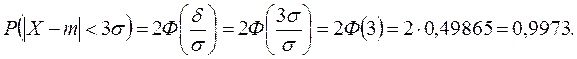ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ФУНКЦИЯ ЛАПЛАСА. ЕЕ СВОЙСТВА
2.1. Функция (интеграл вероятностей) Лапласаимеет вид:
График функции Лапласа приведен на рис.5. Функция Ф(х) табулирована (см. табл. 1 приложений). Для применения этой таблицы нужно знать свойства функции Лапласа: 1) Функция Ф(х) нечетная: Ф(-х)= -Ф(х). 2) Функция Ф(х) монотонно возрастающая. 3) Ф(0)=0. 4) Ф(+¥)=0,5; Ф(-¥)=-0,5. На практике можно считать, что при х³5 функция Ф(х)=0,5; при х£-5 функция Ф(х)=-0,5.
2.2.Существует другие формы функции Лапласа:
В отличие от этих форм функция Ф(х) называется стандартной или нормированной функцией Лапласа. Она связана с другими формами соотношениями:
ПРИМЕР 2.Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами: m=3, s=4. Найти вероятность того, что в результате испытания случайная величина Х: а) примет значение, заключенное в интервале (2; 6); б) примет значение, меньше 2; в) примет значение, больше 10; г) отклонится от математического ожидания на величину, не превышающую 2. Проиллюстрировать решение задачи графически. Решение.а) Вероятность того, что нормальная случайная величина Х попадет в заданный интервал (a,b), где a=2 и b=6, равна:
Значения функции Лапласа Ф(х) определяют по таблице, приведенной в приложении, учитывая, что Ф(–х)= –Ф(х). б) Вероятность того, что нормальная случайная величина Х примет значение меньше 2, равна:
в) Вероятность того, что нормальная случайная величина Х примет значение больше 10, равна:
г) Вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d=2, равна:
С геометрической точки зрения, вычисленные вероятности численно равны заштрихованным площадям под нормальной кривой (см. рис.6).
 Рис. 6. Нормальная кривая для случайной величины Х~N(3;4) Решение.Математическое ожидание случайных ошибок равно нулю m=0. Тогда вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d=15, равна:
ПРИМЕР 4. Автомат изготовляет шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением 0,4 мм, найти, сколько в среднем будет годных шариков среди 100 изготовленных. Решение.Случайная величина Х - отклонение диаметра шарика от проектного размера. Математическое ожидание отклонения равно нулю, т.е. М(Х)=m=0. Тогда вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d=0,7, равна:
Отсюда следует, что примерно 92 шарика из 100 окажутся годными.
ПРИМЕР 5.Доказать правило «3s». Решение.Вероятность того, что нормальная случайная величина Х отклонится от математического ожидания на величину, меньшую d=3s, равна:
ПРИМЕР 6.Случайная величина Х распределена нормально с математическим ожиданием m=10. Вероятность попадания Х в интервал (10, 20) равна 0,3. Чему равна вероятность попадания Х в интервал (0, 10)? Решение.Нормальная кривая симметрична относительно прямой х=m=10, поэтому площади, ограниченные сверху нормальной кривой и снизу интервалами (0, 10) и (10, 20), равны между собой. Так как площади численно равны вероятностям попадания Х в соответствующий интервал, то:
|




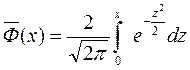 и
и