 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задача 2 Множественная регрессия и корреляция
Задачи для зачёта по эконометрике Задача 1 Парная регрессия и корреляция Пример. По территориям региона приводятся данные за 1991 г. Таблица D.1
Требуется: 1.Построить линейное уравнение парной регрессии 2.Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3.Оценить статистическую значимость параметров регрессии и корреляции с помощью 4.Выполнить прогноз заработной платы 5.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6.На одном графике построить исходные данные и теоретическую прямую. Решение 1.Для расчета параметров уравнения линейной регрессии строим расчетную таблицу D.2. Таблица D.2
Получено уравнение регрессии: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,89 руб. 2.Тесноту линейной связи оценит коэффициент корреляции:
Это означает, что 51% вариации заработной платы ( Качество модели определяет средняя ошибка аппроксимации:
Качество построенной модели оценивается как хорошее, так как 3.Оценку значимости уравнения регрессии в целом проведем с помощью
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы Оценку статистической значимости параметров регрессии проведем с помощью Табличное значение Определим случайные ошибки
Тогда
Фактические значения
поэтому параметры Рассчитаем доверительные интервалы для параметров регрессии
Доверительные интервалы
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 4.Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 5.Ошибка прогноза составит:
Предельная ошибка прогноза, которая в
Доверительный интервал прогноза:
Выполненный прогноз среднемесячной заработной платы является надежным ( 6.В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. D.1):
Рис. D.1. Варианты индивидуальных заданий По территориям региона приводятся данные за 1991 г. Требуется: 1.Построить линейное уравнение парной регрессии 2.Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3.Оценить статистическую значимость параметров регрессии и корреляции с помощью 4.Выполнить прогноз заработной платы 5.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6.На одном графике построить исходные данные и теоретическую прямую. Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Задача 2 Множественная регрессия и корреляция Пример. По
Требуется: 1.Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. 2.Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. 3.Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 4.С помощью 5.С помощью частных 6.Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор. Решение Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:
Найдем средние квадратические отклонения признаков:
1.Вычисление параметров линейного уравнения множественной регрессии. Для нахождения параметров линейного уравнения множественной регрессии
необходимо решить следующую систему линейных уравнений относительно неизвестных параметров
либо воспользоваться готовыми формулами:
Рассчитаем сначала парные коэффициенты корреляции:
Находим
Таким образом, получили следующее уравнение множественной регрессии:
Коэффициенты
Т.е. уравнение будет выглядеть следующим образом:
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации. Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:
Вычисляем:
Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,61% или 0,20% соответственно. Таким образом, подтверждается большее влияние на результат 2.Коэффициенты парной корреляции мы уже нашли:
Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии. При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:
Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи. Коэффициент множественной корреляции определить через матрицу парных коэффициентов корреляции:
где
– определитель матрицы парных коэффициентов корреляции;
– определитель матрицы межфакторной корреляции.
Коэффициент множественной корреляции
Аналогичный результат получим при использовании других формул:
Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом. 3.Нескорректированный коэффициент множественной детерминации Скорректированный коэффициент множественной детерминации
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 4.Оценку надежности уравнения регрессии в целом и показателя тесноты связи
В нашем случае фактическое значение
Получили, что 5.С помощью частных
Найдем
Имеем
Получили, что Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения 6.Общий вывод состоит в том, что множественная модель с факторами
Варианты индивидуальных заданий По 20 предприятиям региона изучается зависимость выработки продукции на одного работника Требуется: 1.Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. 2.Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. 3.Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 4.С помощью 5.С помощью частных 6.Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор. Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
|
-критерия Фишера и 
-критерия Стьюдента.
;
.
.
; 
.
.
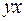
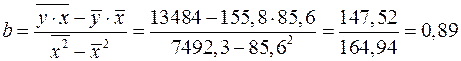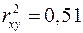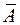не превышает 8-10%.
.
и 
составляет 
. Так как 
, то уравнение регрессии признается статистически значимым.
и 
составит 
.
, 
, 
: 
;
;
.
;
;
.
; 
; 
,
, 
и 
не случайно отличаются от нуля, а статистически значимы.
;
.
параметры 
руб., тогда прогнозное значение заработной платы составит: 
руб.
.
случаев не будет превышена, составит:
.
руб.;
руб.
) и находится в пределах от 131,66 руб. до 190,62 руб.
предприятиям региона изучается зависимость выработки продукции на одного работника 
( 
от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 
( 
.
;
;
.
, 
:
; 
;
.
;
;
.
;
;
.
.
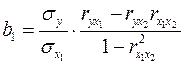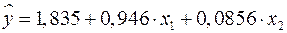и 
стандартизованного уравнения регрессии 
находятся по формулам: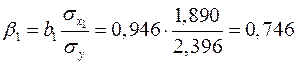
;
.
.
.
; 
.
; 
; 
.
). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.
;
.
,
;
.
.
;
;
.
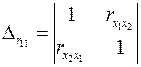
оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 
и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.
) детерминированность результата 
дает 
.
.
(при 
), т.е. вероятность случайно получить такое значение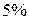 
. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи 
.
;
.
и 
.
;
.
;
.
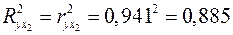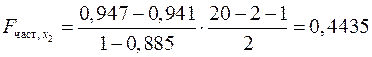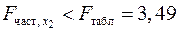. Следовательно, включение в модель фактора 
, т.е. вероятность его случайного формирования меньше принятого стандарта 
. Следовательно, значение частного 
, 
.