 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Примеры по теории вероятностей (с решениями)
Пример.В пачке 10 тетрадей, 8 из которых в клетку. Найти вероятность того, что среди взятых наудачу двух тетрадей есть хотя бы одна в клеточку. Если п - общее число событий данного опыта, определяемых по формуле тогда т - общее число благоприятствующих событий: число событий, когда взята наудачу одна тетрадь в клетку, плюс число событий, когда взяты две такие тетради: Следовательно, вероятность взять наудачу тетрадь в клетку равна: Пример.Вероятность попадания в цель при стрельбе из первой винтовки с оптическим прицелом (событие А) равна 0,9, из второй однотипной винтовки (событие В) равна 0,7. Найти вероятность хотя бы однократного попадания в цель (событие А + В) при одновременной стрельбе из двух винтовок. Так как вероятность попадания в цель при стрельбе из винтовок не зависит друг от друга, то события А и В независимы. След., определим вероятность: р(АВ)=р(А)·р(В)=0,9·0,7=0,63. искомая вер. с учетом совместимости событий А и Вр(А+В)=р(А)+р(В)-р(АВ)=0,9+0,7-0,63=0,97. Пример.На баллистическую экспертизу в одной коробке поступили 7 гильз от автомата отечественного производства, 5 гильз автомата китайского производства и 3 гильзы от автомата польского производства. Найти вероятность того, что первая наугад вынутая гильза окажется от автомата отечественного производства (событие А1), вторая гильза - китайского производства (событие А2) и третья гильза - польского производства (событие А3). Исходя из условия задачи имеем, что р(А1) = По формуле определим искомую вер.: р(А1·А2·А3)= р(А1)·р(А2 /А1)·р(А3 /А1 А2)= Пример.Три курсанта стреляют из пистолета по мишени. Вероятность поражения мишени для первого курсанта равна 0,7, для второго -0,8, для третьего - 0,9. Найти вероятность того, что в мишень попадет хотя бы один курсант. Поражение мишени первым курсантом - А, вторым - событие В, третьим - событие - С. Тогда по условию задачи вероятность непоражения мишени первым курсантом р( Так как противоположные события Следовательно, вероятность поражения мишени хотя бы одним курсантом определится по формуле р(А) = 1 - р( Пример.Три стрелка стреляют по одной и той же цели. Вероятность попадания в цель 1, 2 и 3-го стрелков соответственно равна 0,7, 0,8, 0,9. Найти вероятность того, что все три стрелка попадут в цель. По условию задачи: р(А1) = 0,7; p(A2) = 0,8; р(А3) = 0,9. Так как события: А1, А2, А3 - независимые для одного того же опыта, тогда вероятность попадания в цель 1, 2 и 3-го стрелков определим по формуле: р(А) = р(А1, А2, А3) =р(А1) · p(A2) · р(А3) = 0,7 ·0,8 · 0,9 = 0,504. Пример.На экспертизу поступили три партии одинаковых золотых изделий - по 20 шт. В первой коробке было одно бракованное изделие, во второй - 2, в третьей - 4. Из каждой коробки наугад извлекают по одному изделию. Найти вероятность того, что все три изделия окажутся бракованными (событие А). По условию задачи вероятности p(A1); p(A2); р(А3) извлечения бракованного изделия из каждой коробки есть независимые события для одного того же опыта, тогда вероятность извлечь все три бракованных изделия (событие А) определим по формуле
Пример.Пять курсантов одинаковое количество раз стреляют по отдельным пяти мишеням. Результат стрельбы таков: первый и второй курсанты поражают 3 мишени и имеют 2 промаха - событие B1, третий курсант поражает 2 мишени и имеет 3 промаха - событие В2, четвертый и пятый курсанты поражают 1 мишень и имеют 4 промаха - событие В3. Наугад берется мишень, она оказалась пораженной (событие А). Определить вероятность того, что эта мишень поражена первым курсантом.
По формуле Байеса определяем искомую вероятность: Пример.Имеются три одинаковых конверта. В первом конверте 15 контрольных работ по информатике, во втором - 10 контрольных работ по информатике и 5 контрольных работ по математике, в третьем -15 контрольных работ по математике. Из выбранного наугад конверта вынули контрольную работу по информатике. Найти вероятность того, что контрольная работа взята из первого конверта (А). Из условия задачи имеем: В1 - событие, выбор 1 конверта; В2 -, выбор 2 конверта; В3 -, выбор 3 конверта. Так как выбор каждого конверта равновероятен, то имеем Соответственно вероятность выбора контрольной работы из 1, 2 и 3-го конвертов равна:
Тогда вероятность выбора контрольной работы из первого конверта равна:
Случайные величины. Вер-ть м. рассматриваться в статистическом смысле (как относительная частота появления события при каком-то кол-ве испытаний). Отношение т/п числа т опытов, в которых событие А появилось, к общему числу п проведенных опытов называется частотой события А. При многократном повторении опыта частота события принимает значения, близкие к некоторому числу. Так, испытания, проведенные математиками в XVIII в. с бросанием однородной монеты, показали, что частота выпадения герба незначительно отличалась от числа 0,5.
Под случайной величинойпонимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно, заранее неизвестно). Например: случайная величина X — число дней во взятом наудачу месяце года есть функция элементарных исходов (месяцев), т.е. X (м1) = 31, Х(м2) = 28 или Х(м2) = 29, ..., Х(м12) = 31.
Случайные величины могут быть дискретными или непрерывными: · для дискретной случайной величины множество возможных её значений конечно или счетно, · для непрерывной множество возможных её значений — бесконечно и несчетно.
Возможные значения дискретных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток. Примеры дискретных случайных величин: 1) число родившихся детей в течение суток в Москве 2) число появлений герба при трех бросаниях монеты (возможные значения 0, 1, 2, 3); 3) число произведенных выстрелов до первого попадания 4) число попаданий в самолет, достаточное для вывода его из строя (возможные значения 1, 2, 3, .... п, . . .); Примеры непрерывных случайных величин: 1) дальность полета артиллерийского снаряда 2) расстояние от точки попадания до центра мишени; 3) ошибка измерителя высоты; 4) время безотказной работы радиолампы.
С каждой случайной величиной связано некоторое множество числовых значений, которые она может принимать. В результате испытаний эти значения могут выпадать с различной вероятностью. Правило, устанавливающее связь между возможными значениями сл-й вел-ны и их вероятностями, называется законом распределенияслучайной величины. Закон распределения случайной величины является наиболее полным, исчерпывающим ее описанием.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Итак, пусть случайная величина Xможет принимать одно из п различных значений: х1 х2, … ,хп. При этом каждое из этих значений величина X принимает с определенной вероятностью — соответственно р1, р2, …,рn. Иначе, р1 — это вер. события "случайная величина Xприняла значение х1 илиХ=х1", р2 — вер. случайного события X = х2, и т.д. рп — вероятность случайного события X = хп.
Сведем все эти значения в таблицу:
В первой строке - значения, принимаемые случайной величиной X, во второй строке — их вероятности. Она называется таблицей распределения случайной величины X. Обычно числа в первой строке таблицы распределения располагают в порядке возрастания. Замечание. поскольку в результате испытания величина X наверняка примет одно из этих значений, поэтому для таблицы распределения случайной величины справедливо равенство р1+ р2 + …+рn=1. Итак, для того чтобы при решении конкретной задачи заполнить таблицу распределения заданной случайной величины, надо выписать все принимаемые ею значения х1 х2, … ,хп и вычислить соответствующие вероятности р1, р2, …,рn. Пример с игральным кубиком. Для случайной величинывероятности принять любое из шести значений равны между собой. Таблица распределения выглядит так:
Обратить внимание, что р1+ р2 + …+р6 = 6 ·1/6 =1.
Пример с тремя монетами. В результате одновременного бросания трех монет возможно всего 8 равновероятных исходов: ГГГ, ГГР, ГРГ, ГРР, РГГ, РГР, РРГ, РРР. При 1-м исходе величина Х (число гербов)принимает значение 3; при 2-м, 3-м и 5-м — значение 2; при 4-м, 6-м и 7-м — значение 1; при 8-м — значение 0. С учетом этого таблица распределения случайной величины Y:
Обратить внимание, что р1+ р2 + …+р4 = 2 ·1/8 + 2 ·3/8 =1.
Для более наглядного представления закона распределения часто используется координатная плоскость. По оси Ох отмечают значения, принимаемые случайной величиной, по оси Оу — вер-ти. Затем на плоскости (х, р) отмечают точки и получают столбчатую диаграмму:
Непрерывная случайная величина принимает не какие-либо конкретные числовые значения, а любые значения на числовом отрезке. Описание закона распределения в непрерывном случае существенно сложнее, чем в дискретном.
Главное различие в задачах вычисления вероятностей для дискретного и непрерывного случаев состоит в следующем. В дискретном случае длясобытий типа х = с (случайная величина принимает определенное значение) ищется вероятность р(с). В непрерывном случае вероятности такого типа равны нулю, поэтому интерес представляют вероятности событий типа а ≤ х ≤ b (случайная величина принимает значения из некоторого отрезка). Или для событий типа х ≤ с ищется вероятность р(х ≤ с). Получили график функции распределения F(х ≤ с).
Итак, разнообразие случайных величин весьма велико. Число принимаемых ими значений может быть конечным, счетным или несчетным; значения могут быть расположены дискретно или заполнять интервалы сплошь. Для того чтобы задавать вероятности значений случайных величин, столь различных по своей природе, и притом задавать их одним и тем же способом, в теории вероятностей вводят понятие функции распределения случайной величины. Пусть
Резюмируем сказанное: случайной величиной называется величина, значения которой зависят от случая и для которой определена функция распределения вероятностей.
Мат. ожидание. Мат. ожиданием или средним значением случайной величины называется число, обозначаемое МХ: это среднее ожидаемое значение, принимаемое случайной величиной в больших сериях испытаний. Пример. Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию M x . В данном случае M x = 3,5. Каким образом получилась эта величина? Пусть в N испытаниях
Дисперсия. Дисперсия случайной величины это число DХ = М(Х-МХ)2. Т.о. дисперсия показывает степень отклонения случайной величины от её среднего значения (мат. ожид.). Пример. Дисп: Одним из важных показателей является плотность распределения непрерывной случ. величины.
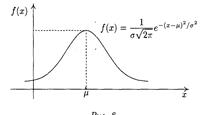
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это — наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Нормальный закон распределения, закон распределения
Нормальный закон распределения говорит о том, что случ. величина может принимать любые значения, и они появляются с различной частотой, но средние и близкие к ним встречаются наиболее часто. По мере удаления от среднего значения случ. величина встречается все реже (плотность распределения падает). График закона нормального распределения – имеет холмообразный вид, симметричен относительно прямой х = МХ (=
Корреляция Одним из важных приложений методов математической статистики является установление зависимости между двумя или более наблюдаемыми величинами. При этом наряду с раздельным анализом выборок, составленных из значений этих величин, возможен и совместный анализ. Рассмотрим ситуацию, когда в результате эксперимента измеряется не одна, а сразу две случайные величины, скажем X и Y. Примерами здесь могут служить врачебный осмотр, где у каждого пациента измеряют рост и вес; измерение средней температуры воздуха в двух городах в течение определенного дня; проверка квалификации рабочих, когда фиксируются производительность и стаж работы. Итак, исходными данными являются пары чисел (точки) (х1, у1), (х2, у2),… (хn, уn), где п — число испытаний. Наряду с анализом величин X и Y по отдельности представляет интерес исследование возможной зависимости между ними. Являются ли величины X и Y независимыми? Если же между ними имеется некоторая зависимость, то какова она? Зависимость на рис. близка к линейной, т. е. точки заметным образом группируются вокруг некоторой прямой. В таких случаях говорят, что величины X и Y коррелированы. Существует простой способ определения степени коррелированности случайных величин. Он основан на вычислении коэффициента корреляции rху. Коэффициент корреляции обладает следующим свойством: -1 Подчеркнем, что коэффициент корреляции отражает степень только линейной зависимости между величинами. Приведем формулы для вычисления rху:
Пример. Рассмотрим проблему, которая стоит перед администрацией некоторого крытого стадиона, где проходят матчи, концерты и др. Перед каждым таким мероприятием требуется оценить, какое количество зрителей придет. Можно предположить, что окончательное число зрителей сильно зависит от того, сколько билетов продано за день до мероприятия. Пусть опыт первых пяти мероприятий этого года таков:
Каков коэфф. корреляции между числом проданных накануне билетов и числом зрителей? Примем число билетов за Х, а число зрителей за У. Найдем коэффициент корреляции.
Этим обстоятельством можно воспользоваться для прогнозирования числа зрителей по имеющейся накануне информации.
|



 ,
,

 ; р(А2 / А1) =
; р(А2 / А1) =  ; р(А3 / А1 А2) =
; р(А3 / А1 А2) =  .
. ) = 1 -0,7 = 0,3, для второго р(
) = 1 -0,7 = 0,3, для второго р(  ) = 1 -0,8 =0,2, для третьего р(
) = 1 -0,8 =0,2, для третьего р( 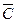 ) = 1 - 0,9 = 0,1.
) = 1 - 0,9 = 0,1.


 .
. ;
;  ;
;  .
.
 — случайная величина и х - произвольное действительное число. Вероятность того, что
— случайная величина и х - произвольное действительное число. Вероятность того, что  . Т.о. мат.ож. показывает, какое значение случайная величина примет в среднем при большом числе испытаний.
. Т.о. мат.ож. показывает, какое значение случайная величина примет в среднем при большом числе испытаний. раз выпало 1 очко,
раз выпало 1 очко,  раз – 2 очка и так далее. Тогда
раз – 2 очка и так далее. Тогда  При N → ∞ количество исходов, в которых выпало одно очко,
При N → ∞ количество исходов, в которых выпало одно очко,  . Аналог.,
. Аналог., 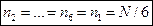 . Отсюда
. Отсюда 

 , и др.
, и др. ).
).

 rху
rху 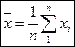





 =
=  (3,5 + 4,6 + 5,8 + 4,2 + 5,2) =
(3,5 + 4,6 + 5,8 + 4,2 + 5,2) =  =
= :
: 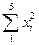 =(3,5)2 + (4,6)2 + (5,8)2 + (4,2)2 + (5,2)2 = 111,73
=(3,5)2 + (4,6)2 + (5,8)2 + (4,2)2 + (5,2)2 = 111,73 
 :
:  = ( 8,1)2 + (9,4)2 + (11,3)2 + (6,9)2 + (9,7)2 = 423,36
= ( 8,1)2 + (9,4)2 + (11,3)2 + (6,9)2 + (9,7)2 = 423,36  :
: 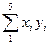 = 3,5· 8,1 + 4,6·9,4 + 5,8· 11,3 + 4,2· 6,9 + 5,2·9,7 = 216,55
= 3,5· 8,1 + 4,6·9,4 + 5,8· 11,3 + 4,2· 6,9 + 5,2·9,7 = 216,55  =
=  Коэффициент корреляции близок к единице.
Коэффициент корреляции близок к единице.