 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Операции над вероятностями.
Суммой п случайных событий называют случайное событие, обозначаемое А1+А2+А3+...+Ап, имеющее место, если произойдет хотя бы одно из этих событий. Например, А=«1-й снег выпал в сент.», В=«1-й снег выпал в окт.», С=«1-й снег выпал в нояб.». Тогда событие (А+В+С)=«1-й снег выпал осенью». Произведением п случайных событий называют случайное событие, обозначаемое А1·А2·А3·...·Ап, имеющее место, если произойдут все эти события. Например, А=«в аудит. вошел студ.», В=«вошел студ.в очках», тогда АВ=«в ауд. вошел студ.в очках». Событием, противоположным А, назовем событие, состоящее в том, что А не произошло ( Например, поражение или непоражение при выстреле мишени - противоположные события.
р(А +В) =р(А) + р(В) - р(А·В) – здесь нам неизвестно р(А·В). Но иногда р(А·В)=0 1)Если А и В не могут произойти одновременно, т.е. А·В невозможное событие, т.е. они несовместимы, тогда р(А·В)=0. Если события А, В попарно несовместимы, то р(А +В) =р(А) +р(В) Пример. В лотерее выпущено 10 000 билетов и установлено: 10 выигрышей по 200р., 100 — по 100р., 500 — по 25р. и 1000 выигрышей по 5р. Какова вероятность того, что 1 билет выиграет не меньше 25р.? Обозначим события: А — «выигрыш не менее 25 р.», А25 — «выигрыш равен 25 р.», Р(А25)= 0,05 А100 — «выигрыш равен 100 р.», Р(А100)= 0,01 А200 — «выигрыш равен 200 р.», Р(А200)= 0,001 Поскольку куплен только один билет, то А= А25+А100+А200. Эти события попарно несовместимы, поэтому Р (А)=0,05 + 0,01 + 0,001 == 0,061.
2) Если А и В могут произойти одновременно, возникает вопрос: насколько наступление одного из них влияет на возможность наступления другого? Бывает, что хотя причинной связи нет, но некоторая зависимость все же присутствует. Например, однократно бросают кубик. Событие А="выпало четное число очков"; событие В="выпало число очков, большее трех". Неверно утверждать, что одно из событий с неизбежностью влечет за собой другое. Но некоторая зависимость имеется. Действительно, всего м.б. шесть исходов: {1, 2, 3, 4, 5, 6}. А - исходы {2, 4, 6}, его вероятность равна 1/2, В - исходы {4, 5, 6). Из этих трех исходов ровно 2 (исходы 4 и 6) входят в событие А. Т. о., если событие В произошло, то вероятность события А равна 2/3. Такая вер-ть назыв условной, и Df р(А /В). В данном примере р(А /В)=2/3. Пример.В урне 3 белых и 4 черных шара. Из урны последовательно вынимают два шара. Найти вероятность того, что второй шар окажется черным при условии, что первый шар был черным. А - "первый шар черный"; В - "второй шар черный". Если произошло событие А, то в урне осталось 6 шаров, из которых 3 черных ® искомая вероятность Пример. Для участия в соревнованиях выделили 9 спортсменов, среди которых 3 - мастера спорта, 3 1-рядники и 3 2-разрядники. Вызывается один спортсмен. Найти вероятность того, что он перворазрядник, если он не был мастером спорта. Здесь имеет место условная вероятность, она равна: р (А/В) = 3/6 =1/2.
3)События независимы - вероятность наступления события В не изменяется в зависимости от наступления или ненаступления события А. Если события А, В независимы, то р(А·В) = р(А) · р(В) и Пример.Соревнования по прыжкам в высоту. Вероятность успешного прыжка у 1-го р(А) = 0,8, а у второго р(В) = 0,9. Какова вероятность того, что оба возьмут предельную высоту? Так как вероятность взятия предельной высоты не зависит друг от друга, то события А и В независимы. Следовательно, р(АВ) = р(А)· р(В) = 0,8· 0,9 = 0,72.
4)Если события А, В зависимы, то вероятность их совместного появления р(А·В) = р(А) · р(В/А) Пример.Из колоды в 32 карты наугад одну за другой вынимают две карты. Найти вероятность того, что: а) вынуты два валета: А — «первая карта — валет», В — «вторая карта — валет». Вероятность совместного появления этих событий, т.е. что вынуты два валета р (А·В)= р(А) · р(B/A) = 4/32 · 3/31 = 3/248. б) вынуты две карты пиковой масти: С — «первая карта пик», D — «вторая карта пик». Вероятность совместного появления этих событий, т.е. что вынуты два карты пиковой масти: р (C·D)= р(C) · р(D/C) = 8/32 · 7/31 = 7/124. в) вынуты валет и дама: А — «первая карта — валет», Е — «втораякарта — дама». Вероятность совместного появления этих событий, т.е. что вынуты валет и дама: р (А·E)= р(А) · р(E/A) = 4/32 · 4/31 = 1/62. Пример.(Тот же) Событие А={2, 4, 6}, р(А)=1/2, событие В={4, 5, 6} р(В)=1/2. р(А/В)=2/3. р (В/А)=2/3. Теперь, событие С={1, 2, 4, 6}, р(С)=4/6=2/3, р(А/С)=2/4 =1/2 и р(С/А)= 2/3 ® р(А/С)= р(А) и р(С/А)= р(С), значит, А и С независимы. Рассмотрим В и С: р(В)=1/2 ≠ р(В/С)=1/4. р(С)=2/3≠р(С/В)=1/4. ® В и С зависимы. Есть ряд событий: А1, А2, А3, ...Ап. Полная группа событий - это совокупность единственно возможных событий опыта, для которой сумма вероятностей отдельных событий А1,А2,...,Ап, образующих полную группу, равна единице: р(А1) + р(А2) +... + р(Ап) = 1 ИТАК.Если события А, В попарно совместимы, то р(А +В) =р(А) +р(В) - р(А·В). Пример.Вероятность сдачи экзамена первым студентом равна р(А) = 0,6, а вторым р(В) = 0,4. Какова вероятность того, что экзамен сдаст хотя бы один студент? События А и В не составляют полную группу событий (++ +- -+ --). Значит, эти события совместимы: р(А + В) = 0,6 + 0,4 - 0,6·0,4 = 0,76. Пример. Определить вероятность того, что при бросании двух монет хотя бы один раз выпадет орел. А –орел на 1 монете, В – на 2 монете. События А и В не составляют полную группу событий (оо рр ор ро). Значит, эти события совместимы: р(А + В) = 1/2 + 1/2 – 1/4 = 3/4. Пример. Определить вероятность того, что при бросании двух игральных костей хотя бы один раз выпадет 6 очков. А - 6 очков при бросании первой игральной кости и В - то же, но для второй игральной кости. События А и В не составляют полную группу событий, т.е. А и Всовместны, Р(А+ В) = Р(А) + Р(В) - Р(АВ) = 1/6 + 1/6 – 1/36 = 11/36.
5)Если есть ряд событий: А1, А2, А3, ...Ап, независимых друг от друга, то
Пример. 4 стрелка одновременно стреляют. Вер. попадания 0,7; 0,75; 0,7; 0,65. Чему равна вер. поражения цели (хотя бы одним стрелком)? Р(А1)=0,7 Р(А2)= 0,75 Р(А3)=0,7 Р(А4)= 0,65. Цель будет поражена, т.е. произойдет событие А1+ А2+ А3+ А4.
Пример. Через остановку пролегают троллейбусный и автобусный маршруты. Трол. подъезжает через каждые 15м. автобус — через каждые 25м. К остановке подходит пассажир. Какова вероятность того, что в ближайшие 10м. на остановке появится троллейбус либо автобус? 1 способ.Вероятность того, что троллейбус появится на остановке в ближайшие 10 минут: р(Т)=10/15=2/3. Вероятность того, что автобус появится на остановке в ближайшие 10 минут: р(А)=10/25=2/5. Вероятность того, что появится автобус или троллейбус: р(А+Т)= 2 способ.Пассажир не уедет в ближайшие 10м.: 3 способ.Можно было воспользоваться формулой:
Пример.Студент пришел на зачет, зная 15 вопросов из 20. Если он не отвечает, то может взять 1 раз другой вопрос. Какова вер. сдать зачет? А1 - вер. взять знакомый вопрос с 1 попытки
А2 - вер. взять знакомый вопрос с 2 попытки
1 способ. Вероятность сдать зачет: р(А)=р(А1)+ р( 2 способ.Вероятность не сдать зачет: р(
6) Формула полной вероятности. Имеется группа несовместимых событий В1, В2, … Вп и некоторое событие А, подразделяющегося на частные случаи А·В1, А·В2, ..., А·Вп так, что Пример.В доме 5 дверей. «А» - человек вошел в дом. «Вi» - человек вошел через i-ю дверь. События Вi несовместимы. Событие А это сумма А·В1+ А·В2+ .... Значит, р(А)= р(А·В1) + р(А·В2) +… (т.е. он вошел или через 1 дверь, или ….) = р(А/В1) · р(В1) + р(А/В2) · р(В2) + … Это и есть формула полной вероятности.
Пример.5 винтовок, на 3 из которых были оптические прицелы. Вероятность поразить мишень при выстреле из винтовки с оптическим прицелом равна 0,9; для винтовки без оптического прицела она равна 0,55. Найти вероятность того, что мишень будет поражена, если курсанту будет предложена наугад взятая винтовка. Из условия примера можно записать: p(B1) = 0,9 - вероятность поражения мишени из винтовки с оптическим прицелом; р(А/В1) = 3/5 = 0,6 - вероятность, что выбрана винтовка с оптическим прицелом; р(В2) = 0,55 - вероятность поражения мишени из обычной винтовки; р(А/В2) = 2/5 = 0,4 - вероятность выбора обычной винтовки. Тогда искомая вероятность будет равна: р(А) = 0,9 · 0,6 + 0,55·0,4 = 0,76.
7) Формула Байеса. Если требуется найти вероятность события Bi когда известно, что А произошло и определено формулой откуда Это и есть формула Байеса в общем виде. Пример.Для пред. задачи:5 винтовок, на 3 из которых были оптические прицелы. Вероятность поразить мишень при выстреле из винтовки с оптическим прицелом равна 0,9; для винтовки без оптического прицела она равна 0,55. Найти, что вероятнее: будут стрелять из винтовки с оптическим прицелом или без него?
Пример.5% мужчин и 0,25% женщин страдают дальтонизмом. И муж., и жен. – одинаковое кол-во. 1)Какова вер-ть того, что наугад выбранный человек – дальтоник? В1 – выбран мужчина. В2 – выбрана женщина. А – человек-дальтоник. Надо найти р(А). р(В1)= р(В2)=0,5. p(A/B1)=0,05 (5%). p(A/B1)=0,0025 (0,25%). По формуле полной вер. получим р(А) = 0,05 · 0,5 + 0,0025·0,5 = 0,02625. 2)Какова вер-ть того, что это человек – мужчина? Надо найти р(В1/А). По формуле Байеса Пример.На экзамене 20 билетов: 5 – легкие и 15 – трудные. 2 студента тянут билет: сначала - первый, потом – второй. 1) какова вер. вытянуть легкий билет у 1 студента? В1 – 1 студент вытянул легкий билет. В2 – 1 студент вытянул трудный билет. А - 2 студент вытянул легкий билет. Надо найти р(В1) = 2) какова вер. вытянуть легкий билет у 2 студента? Надо найти р(А). По формуле полной вер. получим р(А) = р(А/В1) · р(В1) + р(А/В2) · р(В2) = 3) Известно, что 2 студент вытянул легкий билет. Какова вер. того, что и у 1 студента легкий билет? Надо найти р(В1/А). По формуле Байеса |



 ). Сумма вероятностей противоположных событий равна единице: р(А) +р(
). Сумма вероятностей противоположных событий равна единице: р(А) +р(  .
.
 и
и 
 = 1-0,3·0,25·0,3·0,35= 0,992125.
= 1-0,3·0,25·0,3·0,35= 0,992125. .
. . Вероятность, что он уедет 1-1/5=4/5.
. Вероятность, что он уедет 1-1/5=4/5. .
. - вер. взять незнакомый вопрос с 1 попытки
- вер. взять незнакомый вопрос с 1 попытки - вер. взять незнакомый вопрос с 2 попытки
- вер. взять незнакомый вопрос с 2 попытки )= р(
)= р(  . Тогда
. Тогда  Это и есть формула полной вероятности.
Это и есть формула полной вероятности. , здесь выражениер(А) - формула полной вероятности, подставив выражение которой в данное выражение, получим:
, здесь выражениер(А) - формула полной вероятности, подставив выражение которой в данное выражение, получим:  , i и j =1,…n.
, i и j =1,…n. - больше.
- больше.
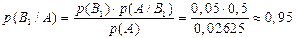 .
.
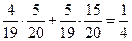 .
. .
.